Мета:

Навчальна: Ввести поняття криволінійної трапеції, визначеного інтеграла, навчити застосовувати формулу НьютонаЛейбніца до обчислення визначеного інтеграла;

Розвиваюча: Формування уявлень про ідеї і методи математики та її роль у пізнанні навколишнього світу, розвиток мислення, розумової активності, пізнавальної самостійності, потреби у самоосвіті;

Виховна: Формування наукового світогляду та загальнолюдських духовних цінностей.

Тип уроку:  комбінований (перевірка раніше здобутих знань і засвоєння нових за допомогою  комп’ютера).

 

Вид уроку:  урок – телеміст.

Конструктор уроку: І. Організаційна частина.

 

ІІ. Перевірка домашнього завдання.  «телерозминка»;  картка – завдання.

 

ІІІ. Актуалізація знань, умінь і навичок.

•      Картка індивідуальних досягнень;

•      картка – завдання «Принцип доповнюваності».

 

IV.   Повідомлення теми, мети і плану уроку. Мотивація навчальної діяльності учнів.

•      Картка – завдання «Інформаційна палітра».

 

V.       Сприйняття та усвідомлення нового матеріалу. (презентація учнівських проектів за допомогою комп’ютерних технологій)

•      Група «Науковців» (учнівська презентація);

•      креативне домашнє завдання з опорними сигналами; групова робота

•      група «Фізиків» (учнівська презентація);

•      група «Практиків» (учнівська презентація);

•      група «Істориків» (історична довідка);

•      група «Журналістів» (творчий пошук «Поезія»).

 

VІ. Перевірка знань учнями фактичного матеріалу.

•      комп’ютерна програма GRAN 2D;

•      інструкційно – технологічна картка.

 

VІІ. Підведення підсумків.

•      Група «Психологів» (рефлексія);  кросворд.

VІІІ. Домашнє завдання. (диференційоване)

•      Обов’язковий мінімум; тренувальні завдання; творчі завдання.

 «Телерозминка»

 (перевірка Д/з)

Картка – завдання №1

Середній рівень

(за кожну правильну відповідь – 0,5 балів)

Заповніть таблицю. 

Функція	xn	1 x	sinx	cos x	1 cos2 x	1 sin2 x
Загальний вигляд первісної

 

Картка індивідуальних досягнень 

 

Прізвище __________                                          Група __________

 

Етапи Роботи	Таблиця первісних	Теорія	Різнорівневі завдання	Обчислення інтегралів	Додаткові бали	Підсумок
Бали

 

Картка – завдання №2

«Принцип доповнюваності» (актуалізація) Середній рівень

(за кожну правильну відповідь – 0,5 балів) Заповніть пропуски у тексті. 

1.     Функція __ називається первісною функції ___ на деякому проміжку, якщо для  всіх  х  із цього проміжку виконується рівність: __________________ . 2.     Нехай функція f має на деякому проміжку первісну. Сукупність усіх первісних для функції f(x) на проміжку називається _________ ___________ цієї функції і позначають _____. Функцію ____ називають _________ _________ . 3.     Нехай функція F(x) є первісною для f(x) на деякому проміжку. Тоді для довільної _________ __ функція _________ також є первісною для функції __ . 4.     Нехай функція __ є первісною для ___ на деякому проміжку. Тоді будь-яка первісна для функції f(x) цьому проміжку може бути записана у вигляді  F(x) + C, де С – деяка стала (число).

 

Картка – завдання №3

«Інформаційна палітра»

Знайдіть невизначений інтеграл. 

І рівень (1 бал)	3  соs2x dx 	Відповідь:
ІІ рівень (2 бали)	cos2xdx	Відповідь:
ІІІ рівень (3 бали)	 (3х 1)dx 	Відповідь:

          

 «Телеміст»

 (сприймання й усвідомлення нового матеріалу)

Група «Науковців»

 

Творча група  самостійно з’ясовувала метод, яким Лейбніц ввів поняття визначеного інтеграла.

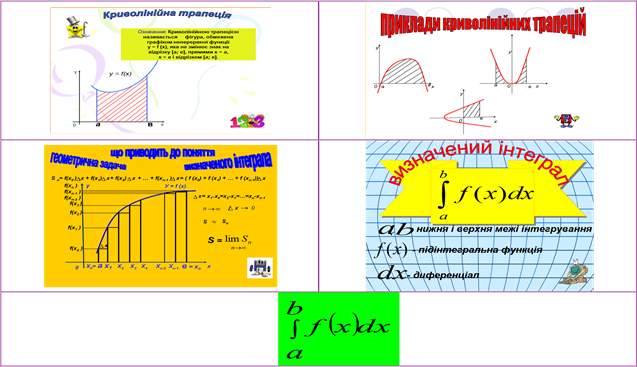
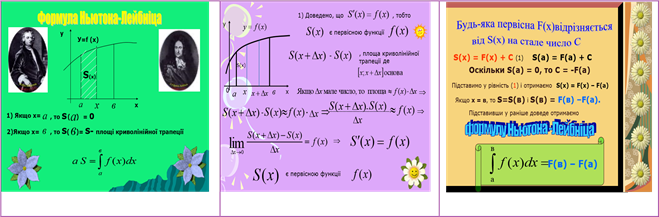
Всі ми вміємо обчислювати площі  прямокутника, трикутника, трапеції, паралелограма, довільного многокутника, а також площі круга та його частин. Виникає питання: як обчислити площу плоскої фігури, обмеженої будь-якою кривою? Виявляється, що розв’язування такої задачі можливе за певних умов, якщо плоска фігура, яку ми розглядаємо – КРИВОЛІНІЙНА ТРАПЕЦІЯ. 

Креативне домашнє завдання з опорними сигналами

 

 

«Телеміст»  (сприймання й усвідомлення нового матеріалу) Група «Фізиків»

 

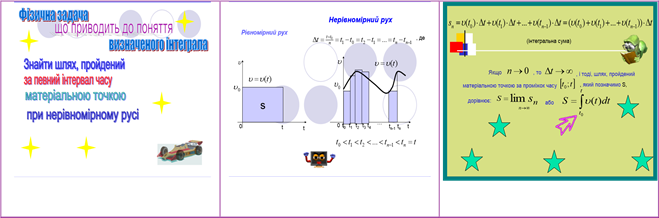
Творча група  самостійно з’ясовувала метод, яким Ньютон ввів поняття визначеного інтеграла.

Креативне домашнє завдання

«Телеміст»

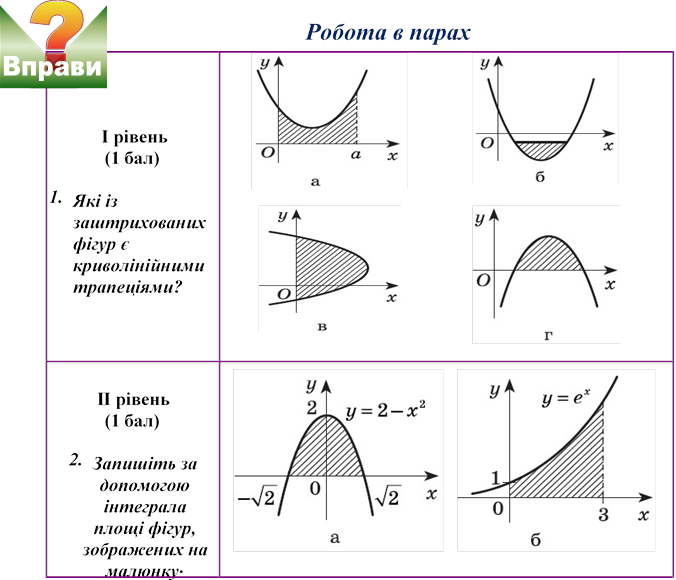
 (сприймання й усвідомлення нового матеріалу) Група «Практиків»

 

Творчій групі стало цікаво, а як обчислюється визначений інтеграл? 

Креативне домашнє завдання

 

«Телеміст»

 (сприймання й усвідомлення нового матеріалу)

Група «Істориків» Креативне домашнє завдання

 

Творча група готувала історичну довідку про І.Ньютона та Г. Лейбніца.

 

―Розумом він перевершив рід людський ‖ – ці слова написані нащадками про видатного англійського науковця, фізика і математика Ісаака Ньютона. Поряд з Ісааком Ньютоном стоїть ім'я німецького вченого Готфріда Лейбніца, який залишив після себе наукові праці у філософії, математиці, юриспруденції, логіці, дипломатії, політології. Ісаак Ньютон і       Готфрід Лейбніц завершили теорію

диференціального та інтегрального числення, що дало

можливість швидко і просто розв'язувати задачі, які раніше вважалися неприступними. Завдяки зручній загальній теорії можна швидко будувати дотичні до найскладніших кривих, знаходити найбільші та найменші значення функції, обчислювати площі різноманітних фігур, об'єми просторових тіл, розв'язувати різні фізичні задачі. 

«Телеміст»

 (сприймання й усвідомлення нового матеріалу) Група «Журналістів»

 

Творча група буде висвітлювати основні моменти сьогоднішнього телемосту.

bb FbFa  f xdxFxa a

Творчий пошук «Поезія»

 

Ньютон і Лейбніц

 

Які натхненні Ньютон з Лейбніцем були,

Якими барвами їх формули заграли,

Яку могуть побачили, коли Зійшлись їх похідні і інтеграли!

Зійшлись – немов злилися два струмки В стократ потужнішу ріку єдину.

Їх теоремі давній завдяки

Те, що колись долали вчені за віки, Тепер школяр долає за годину.

 

Виконайте завдання за допомогою комп’ютерної програми GRAN 2D .

 

Пам’ятайте про техніку безпеки при роботі за комп’ютером

 

Достатній рівень

(за кожну правильну відповідь – 1 бал)

3 а)  х3dx; 1

 4 б)  cos2 x ; 0

2 в)  (3х-1)dx; 1

1 г) (х2)2dx . 5

 

«Телеміст»

 (рефлексія)

Група «Психологів»

 

Досліджували вплив отриманої інформації на розумові здібності індивідуумів.

 

 Що нового ви Чи сподобався       дізналися під вам урок – телеміст? час уроку?

 

 

 

А як засвоїли матеріал, перевіримо за допомогою кросворда. Високий рівень (3 бали)

1.     Першу букву якого слова нагадує знак інтеграла? 

2.     Хто із відомих математиків-фізиків розглянув фізичний зміст інтеграла? 

3.     Хто із відомих математиків розглянув математичний зміст інтеграла? 

4.     Як називається трапеція, площу якої ми знаходимо за допомогою визначеного інтеграла? 

5.     Як називається функція, яка стоїть пі знаком інтеграла? 

6.     Як називається множник dx в підінтегральному виразі?

7.     Як називається операція обернена до операції диференціювання?  

Домашнє завдання (диференційоване)



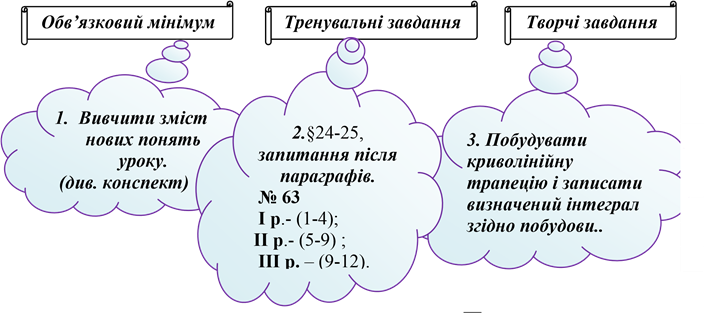
2

Індивідуально.    Обчислити: cos5xcos3xdx

                                                                                                                                                                  

8

«Опорний конспект»  на тему: 

«Визначений інтеграл та його застосування»

 

1. Обчислення визначеного інтеграла (Формула Ньютона - Лейбніца)
Формула				Приклад
Якщо функція f (x) визначена і не- перервна на відрізку [a; b], а F (x)— довільна її первісна на цьому відрізку (тобто FR (x) = f (x)), то				Оскільки для функції f x x2 однією з первісних є Fx x3 , то 3 2            x3 2    23 13       7     1 x2dx 3 1  3  3 323. 1
	bb FbFa  f xdxFxa a
2. Криволінійна трапеція
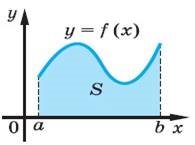
Означення				Ілюстрація
Нехай на відрізку [a; b] осі Ox зада- но неперервну функцію f (x), яка набуває на цьому відрізку тільки невід’ємних значень. Фігуру, обме_ жену графіком функції y = f (x), відрізком [a; b] осі Ox і прямими x = a і x = b, називають криволі_ нійною трапецією.
3. Площа криволінійної трапеції
Формула		Приклад
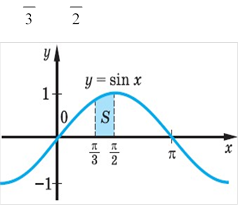
b  f xdx a		Обчисліть площу фігури, обмеженої лініями y = sin x,  y = 0, x,x Розв’язання  Зображуючи ці лінії,бачимо, що задана фігура —                           криволінійна трапеція.                    2                            2  S   sin xdx  cos x                                            3                                              3

«Опорний конспект»  на тему: 

«Визначений інтеграл та його застосування»

 

4. Властивості визначних інтегралів
a  f xdx0 a	b              a  f xdx f xdx a              b		b                     b                 b f xgxdx  f xdx gxdx a                     a                 a
b                   b k f xdxk  f xdx a                   a		Якщо функція f (x) інтегрована на [a; b] і c   [a; b], то
			b             c                 b  f xdx  f xdx f xdx a             a                 c
5. Означення визначеного інтеграла через інтегральні суми
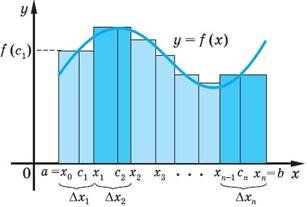
				Нехай функція f (x) — неперервна на відрізку [a; b]. Виконаємо такі операції. 1.               Розіб’ємо відрізок [a; b] на n відрізків точками x1, x2, ..., xn – 1 (вважаємо, що a = x0, b = xn). 2.               Позначимо довжину першого відрізка через Δx1, другого — через Δx2 і т. д. (тобто Δx1= x1 – x0, Δx2= x2 – x1, ..., Δxn= xn – xn– 1).
3.               На кожному з одержаних відрізків виберемо довільну точку ci (тобто ci    [xi – 1; xi] , де i = 1, 2, ..., n). 4.               Складемо суму Sn = f (c1) Δx1+ f (c2) Δx2+ ... + f (cn) Δxn. Цю суму називають інтегральною сумою функції f (x) на відрізку [a; b]. b  f xdx a Якщо n →∞ і довжини відрізків розбиття прямують до нуля, то інтег- ральна сума Sn прямує до деякого числа, яке і називають визначеним інтегралом функції f (x) на відрізку [a; b] і позначають   .