І рівень (1 бал)

Обчисліть інтеграл:

                 2                                       3                                         

         a) xdx;       b⁾x²dx;         c)cos xdx.

                ^{0                     0                       2}

Відповідь:

ІІ рівень (2 бали)

Відомо, що                      Знайдіть :

               b                                                                     a

 f xdx 4          f xdx a                             b                     

Відповідь:

ІІІ рівень (3 бали)

Обчисліть :

2

5x  2^dx.

1

Відповідь:

xn

1

x

sinx

cos x

1 cos² x

1 sin² x

ех

ах

Приклад 1

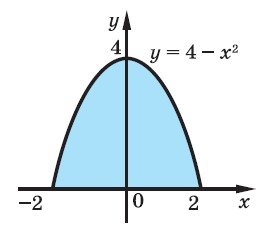
Обчисліть об’єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої лініями  y⁰, та y4x².

Розв’язання

Коментар

1.             Знайдемо абсциси точок перети- ну заданих ліній. 4x² 0,x2

2.             Оскільки задана фігура — криво- лінійна трапеція, то об’єм тіла обер- тання дорівнює

3.  

                    2                                                          2

V  _4 x²²dx _168x²  x⁴dx 

                   2                                                       2                                                             

2

                      x³           x⁵              4

16x 8 3  5 2  76 5.



1.               Зобразимо задану фігуру і впевнимося, що вона є криволіній-

ною трапецією. 

2.               У цьому випадку об’єм тіла обертання можна обчислювати за готовою формулою

                           b                                             b

V f ²xdx  f ²xdx

                           a                                             a

3.               Щоб знайти межі інтегрування, достатньо знайти абсциси точок пе- ретину заданих ліній.

4.               Як і для задач на обчислення площ, до відповіді записують число- ве значення об’єму, але можна під- креслити, що ми одержали саме ве-  личину об’єму, і записати

відповідь: 76⁴

⁵ куб. од. (тобто 

кубічних одиниць).

Знайдіть об’єм тіла, утвореного обертанням навколо осі абсцис криволінійної трапеції, обмеженої лініями:

1 y  x² 1 , y⁰,x⁰,x1

Укажіть формулу за допомогою якої можна обчислити об’єм фігури:

Молодці! Я вами задоволена.

50 X 50

Ви можете краще.

3. Об'єми тіл

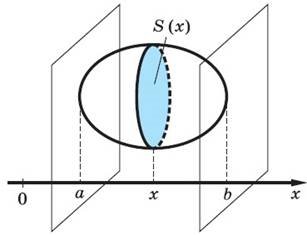
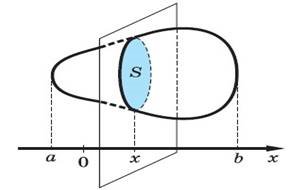
Якщо тіло вміщене між двома перпендикулярними до осі Ох площинами, що проходять через точ-

ки х = а і x = b, то 

де S (x) — площа перерізу тіла пло- щиною, що проходить через точку х  [a; b] і перпендикулярна до осі Ох.

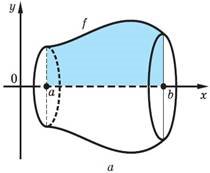
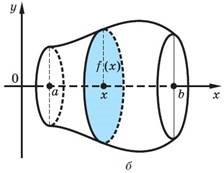
Якщо тіло одержане в результаті обертання навколо осі Ох

криволінійної трапеції, яка обмежена графіком неперервної і невід’ємної на відрізку [a; b] функції у = f (x) і прямими х = а і x = b, то

Приклад