Урок "Множество и его элементы. Подмножества. Урок № 5"

Урок № 5         § 13

Тема: Множество и его элементы. Подмножества.   

Цель урока:

Образовательная: дать учащимся определение множества и подмножества, элементы множества. Ввести понятие диаграмма Эйлера.

Развивающая: развивать вычислительные навыки и умение. Развивать творческие способности и логическое мышление.  

Воспитательная: воспитание трудолюбия и упорства в достижении цели

Тип урока: урок усвоения новых знаний и умений

Оборудование: мел, учебник, цветные мелки

Х о д   у р о к а

1. Организационный момент.

- проверка готовности класса к уроку;

- проверка готовности учащихся к уроку;

- приветствие

2. Актуализация знаний. Проверка д/з.

 Анализ домашней работы у доски

  I ученик № 387(2,4,7);

  II ученик  № 388(2,4,6);

  III ученик № 389(2,4,6,8);

  IV  ученик № 390(2,4,6).

 Пока учащиеся у доски готовят ответы, весь класс работает над повторением теоретического материала  § 14:

 - Что называем квадратным корнем из числа а? (Квадратным корнем из числа а называется число, квадрат которого равен а)

 - Что называем арифметическим квадратным корнем из числа а?                     (Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а)

 - Сколько квадратных корней имеет число 36? А число 7?

 - Сколько арифметических квадратных корней имеет число 64? А числа: 81; 13; - 25?

 Выслушиваем решения домашней работы, корректируя, задавая им вопросы и исправляя ошибки совместно с учащимися всего класса.

3. Подача нового материала.

Мотивация. Вы любите математику (только честно)? А почему не любите? Не интересна, трудна, скучна. Я, сейчас, попробую доказать вам обратное.

-Вы кто? (человек, школьник, учитель, Лена, мама, дочь…)

-Хорошо. Один ученик, две Саши, один учитель…А, вместе мы? Люди. Вместе нас много. В математике есть такое понятие, как … множество. Каждый из нас элемент, какого либо множества. Множество людей, множество учеников, множество учителей… Продолжите перечень множеств. А, что же, учителя, ученики и т.д. не люди?!

     Встаньте вокруг синего обруча представители мужского пола,  вокруг красного представители женского пола, а вокруг желтого Игорь. Что, не можем определиться, куда нам: к умным или красивым?! Какой выход из положения можно предложить? (образовать пересечение этих множеств) В математике это понятие называется пересечением множеств. Поэтому, и получается, что один и тот же человек или предмет может оказаться элементом сразу нескольких множеств. Поэтому, так многообразен и удивителен наш мир.

Теоретический материал.

I.  Множество представляет собой совокупность некоторых предметов или чисел, составленных по каким-либо общим свойствам или законам (множество букв на странице, множество правильных дробей со знаменателем 5, множество звезд на небе и т.д.).

Для записи множества используют фигурные скобки: 

«{ »- множество открывается; 

"}" — множество закрывается.

А само множество называют заглавными латинскими буквами: А, В, С и так далее.

Примеры.

1. Записать множество А, состоящее из всех гласных букв в слове  «математика».

Решение.  А={а, е, и}.  Вы видите: несмотря на то,что в слове «математика» имеется три буквы «а» — в записи множества повторений не допускается,  и буква «а» записывается только один раз. Множество А состоит из трех элементов.

2. Записать множество всех правильных дробей со знаменателем 5.

Решение. Вспоминаем: правильной называют обыкновенную дробь, у которой числитель меньше знаменателя. Обозначим через В искомое множество. Тогда:

 Множество В состоит из четырех элементов.

  В = {  }

II. Множества состоят из элементов и бывают конечными или бесконечными. Множество, которое не содержит ни одного элемента, называют пустым множеством и обозначают Ø. 

III. Множество В называют подмножеством множества А, если все элементы множества В являются элементами множества А. 

3. Какое из двух данных множеств В и С является подмножеством множества К,

если В={-1; 3; 4}, C={0; 3; 4; 5), K={0; 2; 3; 4; 5; 6} ?

Решение. Все элементы множества С являются также элементами множества К, поэтому, множество С является подмножеством множества К. Записывают:

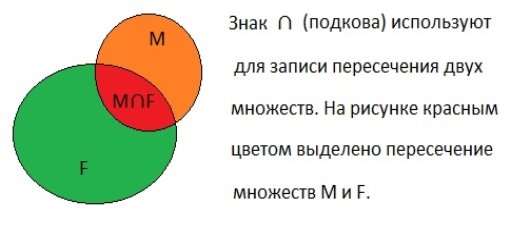
IV. Пересечением множеств А и В называется множество, элементы которого принадлежат и множеству А и множеству В.

4. Показать пересечение двух множеств М и F с помощью кругов Эйлера.

Решение. 

V. Объединением множеств А и В называется множество, элементы которого принадлежат хотя бы одному из данных множеств А и В.

5. Показать с помощью кругов Эйлера объединение  множеств Т и Р.

Решение.

4. Закрепление материала.

В классе рассмотрим следующие номера: №422, 423, 436, 431, 434

5. Физкультминутка.

Быстро встали, улыбнулись

Выше-выше потянулись

Ну-ка плечи распрямите,

Поднимите, опустите.

Вправо, влево повернитесь,

Рук коленями коснитесь.

Сели, встали. Сели, встали.

И на месте побежали.

Молодцы. Садитесь.

6. Самостоятельная работа

Решить № 428

(подсказка: необходимо сперва решить уравнения, найти корни и записать их в виде множества).

7. Итоги урока. Рефлексия.

  Подведение итогов и оценивание учащихся.

- Над какой темой работали?

- Какие цели ставили в начале урока?

- Что  узнали нового? 

6. Домашнее задание  § 13,  № 424, 427, 429, 432.

https://infourok.ru/razrabotka_uroka_po_teme_mnozhestva._podmnozhestva._operacii_nad_mnozhestvami.-357511.htm