Урок №1 "Логарифм і його властивості"
Урок №1
Тема уроку. Логарифми та їх властивості.
Мета уроку. Формування поняття логарифма числа. Познайомити учнів з основною логарифмічною тотожністю. Розвивати самостійність логічного мислення. Виховувати культуру математичних записів, вміння застосовувати знання в нестандартних ситуаціях.
Тип уроку. Вивчення нового матеріалу.
Хід уроку
І. Організаційна частина
ІІ. Мотивація навчальної діяльності
Проблемний метод, колективна форма роботи.
Учні, розв’яжіть, будь ласка, рівняння: ![]() і дайте відповіді на такі запитання:
і дайте відповіді на такі запитання:
- Яким способом краще розв’язати таке рівняння?
- Чи має таке рівняння корені і скільки?
- Який цей корінь?
(відповіді учнів)
ІІІ. Вивчення нового матеріалу
Пояснення вчителя.
Корінь рівняння ![]() домовились називати логарифмом числа 5 з основою 2 і позначати
домовились називати логарифмом числа 5 з основою 2 і позначати ![]() Таким чином, число
Таким чином, число ![]() – це показник степеня, до якого треба піднести число 2, щоб отримати число 5. Можна записати:
– це показник степеня, до якого треба піднести число 2, щоб отримати число 5. Можна записати:
![]()
Означення. Логарифмом додатного числа b з основою a, де a>0 і a ![]() 1, називають показник степеня, до якого потрібно піднести число a, щоб отримати число b.
1, називають показник степеня, до якого потрібно піднести число a, щоб отримати число b.
Приклад.
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() =0.
=0.
З означення логарифма випливає, що при a>0, a ![]() 1 і b>0 виконується рівність
1 і b>0 виконується рівність
![]()
Її називають основною логарифмічною тотожністю.
Дію знаходження числа с за даними числами а і ![]() , де a>0, a
, де a>0, a ![]() 1 і b>0, називають логарифмуванням числа
1 і b>0, називають логарифмуванням числа ![]() за основою а. (
за основою а. (![]() ). При b
). При b![]() 0 вираз
0 вираз ![]() немає змісту.
немає змісту.
Десятковими логарифмами називаються логарифми за основою 10, позначаються lg.
Наприклад, lg100 = 2, lg0,0001 = - 4.
Натуральними логарифмами називаються логарифми за основою е (число е — ірраціональне, е == 2,718281828459045...), позначаються ln.
Наприклад: ln е = 1, ln е2 = 2, ln ![]() = -1.
= -1.
ІV. Закріплення нового матеріалу
Вправа 19.1.
Чи правильною є рівність:
-
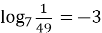 ;
;
-
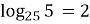 ;
;
-
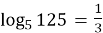 ;
;
-
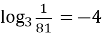 ;
;
-
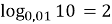 ;
;
-
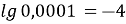 ;
;
-
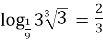 ;
;
-
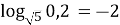 .
.
Цю вправу учні розв’язують усно, використовуючи метод ПРЕС. Завдання учнів: пояснити розв’язання вправи, використовуючи слова «Я вважаю, що… тому що…наприклад…. отже, таким чином…»
Вправа 19.2. (п. 1-4)
Знайти логарифм з основою 2 числа:
-
1; 2) 2; 3) 32; 4)
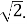
Вправу розв’язуємо, використовуючи метод розв’язування перших задач. А саме, вчитель записує розв’язок на відкидній дошці, пояснює його, дошку закриває, учні відтворюють розв’язання в своїх зошитах. Після цього обмінюються зошитами і перевіряють задачу, звіряючи з відкидною дошкою.
Вправа 19.4.(п. 1-4)
Знайти логарифм з основою ![]() числа:
числа:
-
1; 2)
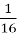 ; 3)
; 3) 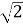 ; 4) 64.
; 4) 64.
Дану вправу учні розв’язують колективно із записом у зошитах.
Вправа 19.7.(п.1-4)
Чому дорівнює логарифм числа 10000 з основою:
- 10; 2) 100; 3) 0,1 4) 1000.
Дану вправу учні розв’язують ланцюжком біля дошки.
Вправа 19.9.
Розв’яжіть рівняння
-
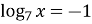 ;
;
-
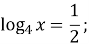
-
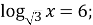
-
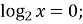
-
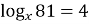 ;
;
-

Рівняння учні розв’язують по групах.
Відповіді: 1) ![]() ; 2)
; 2)![]() ; 3) 27; 4) 1; 5) 3; 6)
; 3) 27; 4) 1; 5) 3; 6) ![]() .
.
Вправа 19.37 (індивідуально)
При яких значеннях х є правильна рівність:
-
 .
.
Розв’язання:
За означенням логарифма маємо, що під логарифмічний вираз повинен бути більшим 0, звідси випливає:
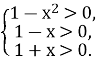
Розв’язавши систему нерівностей отримаємо: х![]()
Відповідь: ![]() .
.
Розв’язання:
За означенням логарифма маємо, що під логарифмічний вираз повинен бути більшим 0, звідси випливає, що ![]() завжди додатнє, оскільки це є квадрат двочлена і
завжди додатнє, оскільки це є квадрат двочлена і ![]() також завжди більше нуля. Тому потрібно виключити значення, яке перетворює підлогарифмічний вираз в нуль. Це значення x=2.
також завжди більше нуля. Тому потрібно виключити значення, яке перетворює підлогарифмічний вираз в нуль. Це значення x=2.
Відповідь: ![]()
«На замітку абітурієнту»
В цій рубриці представленні завдання, які були на ЗНО попередніх років
1). Обчисліть ![]()
![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
Правильна відповідь: А.
-
Обчисліть
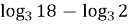
Правильна відповідь: 2 (вказівка: за властивістю логарифма)
V. Підведення підсумків уроку.
Контрольні запитання
1. Дайте означення логарифма додатного числа b за основою а ( а > 0, а≠ 1).
2. Який логарифм називають десятковим логарифмом і який натуральним логарифмом?
3. Сформулюйте основну логарифмічну тотожність.
VІ. Домашнє завдання
- Опрацювати п.19, ст.181(А.Г.Мерзляк). Вивчити означення логарифма.
- Виконати вправи: № 19.3, 19.10 - письмово. додатково № 19.12.


про публікацію авторської розробки
Додати розробку
