Презентація. 11 клас. Елементи математичної статистики
Про матеріал
Презентація "Елементи математичної статистики" для використання на уроці засвоєння нових знань та при підготовці до ЗНО. Містить визначення основних понять математичної статистики: обсяг, розмах, мода, медіана, середнє значення вибірки та приклади їх знаходження. Графічне представлення (полігон частот, гістограма) вибірки. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку











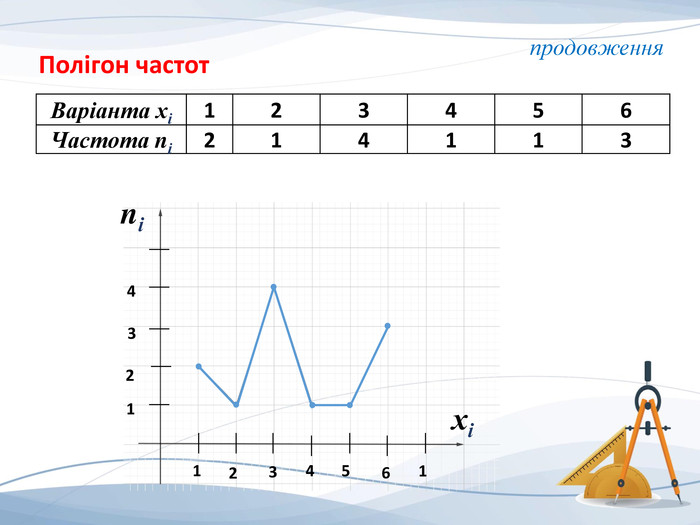
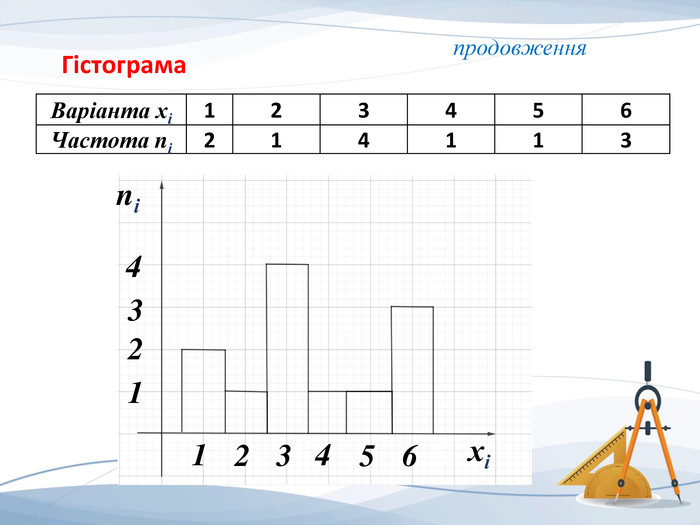












-

Кольчак Марина
12.05.2025 в 23:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Щербань Татьяна
21.04.2025 в 14:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кобилинський Богдан
15.04.2025 в 13:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Палій Олена Григорівна
09.03.2025 в 11:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Фінашина Наталія Миколаївна
18.02.2025 в 20:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kлачик Альона Ярославівна
18.01.2025 в 14:45
Чудова презентація:) дякую за можливість скористатися
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пашечко Анастасия
29.04.2024 в 00:56
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Заклюка Людмила Федорівна
12.03.2024 в 14:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

П'ятковська Світлана
07.03.2024 в 20:14
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Корнацька Людмила Леонідівна
12.02.2024 в 09:14
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шах Руслана Вікторівна
06.02.2024 в 12:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гіщинська Марія Володимирівна
07.04.2023 в 16:53
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Прошак Сергій Володимирович
13.12.2022 в 05:48
Щиро дякую:))
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гелешко Наталія
21.04.2022 в 21:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тимошенко Тетяна Іллівна
04.04.2022 в 00:19
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Харченко Ірина Вікторівна
21.03.2022 в 20:10
Дякую за змістовну презентацію!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чубарь Елена
16.02.2022 в 00:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kalynyuk Svitlana
14.02.2022 в 23:07
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лещенко Олена
31.10.2021 в 22:44
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 16 відгуків