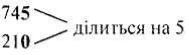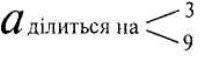Урок "7 клас урок 6 з математики"
І.Подільність чисел Тема 1. Подільність чисел. Прості і складені числа.
Урок № 2
Тема. Ознаки подільності чисел
Мета: систематизувати інтуїтивні знання учнів про ознаки подільності, відомі їм з початкової школи (подільність на 2, 5, 10) та доповнити ці знання ознаками подільності на 3 і 9.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Перевірка домашнього завдання
-
Домашнє завдання перевірити, викликавши 4-х учнів до дошки або
залучивши на допомогу учнів-консультантів. - Бліц-опитування (У цей час учні біля дошки готують розв'язання домашніх вправ)
Методика проведення
Учні дають короткі письмові відповіді у вигляді символів, які означають: «+» — так; «—» — ні; «0» — не знаю.
Запитання до класу
Чи правда, що:
- 32— дільник 16;
- 48 кратне 8;
- 1; 2; 5 — усі дільники числа 10;
- 1 — просте число;
- сума всіх дільників числа 8 дорівнює 15;
- якщо натуральне число більше за 1 і воно не просте, то воно складене?
Після виконання роботи обов'язково має проводитись перевірка і повторення основних теоретичних понять попереднього уроку.
II. Мотивація пізнавальної діяльності
Коротка евристична бесіда, зміст якої приблизно такий.
Шановні учні! Ви вже знаєте, що означає поняття «число а ділиться на число b». Як же можна перевірити, чи справджується це твердження для даних двох натуральних чисел? (Поділити а на b, і якщо частка — натуральне число, то відповідь ствердна.) Чи не існує якихось інших способів перевірити подільність а на b? Чи обов'язково треба ділити 288 на 2; 150 на 10; 2 365 на 5, щоб довести подільність цих чисел? (Ні, за певними ознаками ми бачимо, що перше число в кожній з пар ділиться на друге.)
III. Систематизація і доповнення знань
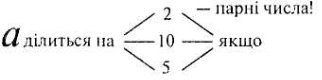
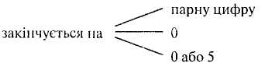
Після проведеної бесіди учні готові сприймати (а може, і самостійно сформулювати ознаки подільності чисел на 2, 5, 10 (див. конспект 2)). Після виконання відповідних записів учнями в зошитах учителю слід ще раз звернути увагу учнів на те, що, використовуючи ці ознаки подільності, ми «звертаємо увагу» тільки на останню цифру.
Ознаки подільності на 3 і 9 учитель формулює самостійно і для допитливих учнів доводить їх. Результати записуються до конспекту 2.
|
Конспект 2 |
|
|
Ознаки подільності |
|
|
|
|
|
Приклад 196 ділиться на 2 210 ділиться на 10
|
|
|
|
|
|
|
Приклад 582 ділиться на 3, бо 5 + 8 + 2 = 15, 15 ділиться на 3 189 ділиться на 9, бо 1 + 8 + 9 = 18 ділиться на 9 |
Кмітливі учні (або вчитель) зауважують, що одне й те саме число може ділитись одночасно на кілька з названих чисел (на 2 і на 5, на 3 і на 5, на 9 і на 2), що може означати виконання подільності й на інші числа (подільність на 3 і на 5 означає подільність на їх добуток, тобто на 15 і т. ін.).
IV. Закріплення знань
І рівень
Усні вправи
Про які з названих чисел 1; 2; 10; 15; 100; 102; 900 можна сказати, що вони:
а) парні;
б) непарні;
в) діляться на 10;
г) діляться на 5;
д) діляться на 3;
є) кратні 9?
ІІ, IIIрівні
Письмові вправи
- З чисел 122 175; 188 154; 291 523; 510 577; 941 220 і 977 895 випишіть ті, які:
а) кратні 5;
б) діляться на 9;
в) діляться на 5 і на 9;
г) не діляться ні на 2, ні на 3.
-
Замість зірочок поставте цифру, щоб число ділилось на 3 (на 9).
а) 35*12;
б) 72*331;
в) 4*07.
- Випишіть:
а) парні натуральні числа, менші за 20;
б) непарні натуральні числа, не більші за 21;
в) усі парні двоцифрові числа, що мають у складі цифру 7;
г) найбільше трицифрове число, що ділиться на 9;
д) найменше трицифрове число, що ділиться на 3.
Додатково. Вправи на повторення
а) Напишіть число, яке є дільником чисел: 15 і 18; 40 і 60; 12 і 24; 16 і 21.
б) Знайдіть значення виразу (403 · 804 – 71 370 : 234) · 14 + 1428.
в) Розв'яжіть задачу.
Площа поля 520 га. За добу було зібрано врожай з площі, що становить 28% площі поля. З якої площі у гектарах було зібрано врожай?
V. Підсумок уроку
Запишіть у кожну з клітинок таблиці по одному натуральному числу, яке задовольнило б обидві умови.
|
Число |
Парне |
Непарне |
Кратне 5 |
Кратне 3 |
|
Просте |
|
|
|
|
|
Складене |
|
|
|
|
VI. Домашнє завдання
- Напишіть 5 найменших трицифрових чисел, які діляться на 10.
- Які з чисел 5, 95, 130,54, 108,5 551, 10 000 діляться на 5?
- Які з чисел 9, 36, 45, 333, 447, 10 009 не діляться на 2?
- Які з чисел 504, 735, 1 002, 2 037, 7236 діляться на З?
- Які з чисел 405, 738, 2 001, 7 704, 333 діляться на 9?
-
Знайдіть усі спільні дільники чисельника і знаменника дробу
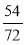 .
.
1


про публікацію авторської розробки
Додати розробку