Урок "Тождественные преобразования выражений, содержащих квадратные корни. Урок №9"

Урок № 9         §2, п. 16

Тема: Тождественные преобразования выражений, содержащих квадратные корни  

Цель урока:

Образовательная:  закрепить основные свойства квадратных корней, дать учащимся  различные способы преобразования выражений с корнями.

Развивающая:  развитие вычислительных навыков и умственных способностей.

Воспитательная: воспитание трудолюбия и активной жизненной позиции.

Тип урока: урок усвоения новых знаний и умений

Оборудование: учебник

Х о д   у р о к а

1. Организационный момент

- проверка готовности класса к уроку;

- проверка готовности учащихся к уроку;

- приветствие

2.  Мотивация урока.

Сегодняшний урок я хотела начать с философской загадки Вальтера: Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и краткое, самое дорогое, но и дёшево ценимое нами? (время).

Итак, у нас всего 45 минут и мне очень хотелось, чтобы это время пролетело для вас незаметно, но с пользой.

3.  Проверка Д/З

    Анализ д/з № 476, 478, 482– устный обзор.

    Особо обращаем внимание на такое задание. Преобразовать , если     a < 0

   Т.к. a < 0, то = 3 ∙ |a| = 3 ∙ (- a) = - 3a.

Дать учащимся ещё раз понять, что выражение - 3a положительно при a < 0 и значение арифметического квадратного корня тоже всегда неотрицательно.

4. Объяснение нового материала

Как вы знаете, алгебра в основном занимается преобразованием выражений. Выражения с квадратными корнями можно  также складывать, вычитать, умно­жать, возводить в степень и делить (на де­литель, отличный от нуля).

  Так, например:

  + - 13 = -4   - это сложение иррациональных выражений мы называем приведением подобных слагаемых; (это подобно тому, как выполнить сложение 3х + 6х – 13х).

  ∙ = 30    - умножение иррациональных выражений; (при этом можно сказать, что воспользовавшись сочетательным свойством умножения, необходимо умножить рациональные числа с рациональными числами, а иррациональные числа с иррациональными числами, т.е.

  ∙ = 5 ∙ 6 ∙ = 30).

  24 : 8 = = 3   - деление или с другой стороны это

       сокращение дроби;

   = 16 ∙ 11 = 176    - возведение в степень произведения

     рационального и иррационального числа.

     Рассмотрим и другие преобразования выражений с корнями.

  = = ∙ = 5;

  = = 10;

  = = 9∙3 = 27 .

   Подобное преобразование называют вынесением множи­теля за знак корня.

   В первом примере за знак корня вы­несен множитель 5.

  Во втором примере за знак корня вы­несен множитель 10.

   В последнем примере за знак корня вы­несены множители 9 и 3.

Преобразование, обратное вынесению множителя за знак корня, называют внесением множителя под знак корня.

  Например.

  = ∙ =      или   = ∙ =

   В этом примере под знак корня вносим множитель 3. Рассмотренные преобразования осуществляются на основа­нии теоремы о корне из произведения.

   Если знак корня находится в знаменателе дроби, то та­кую дробь можно заменить тождественной, знаменатель ко­торой не имеет корней. Достаточно умножить члены дроби на соответствующее выражение, применяя основное свойство дроби.

  Например.

  = = = ;

  = = = = .

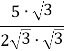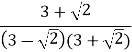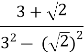Такие преобразования называют освобождением дроби от иррациональности в знаменателе.

Подобно вышесказанным, такие преобразования можно выполнять также с выраже­ниями, содержащими переменные.

   Например.

  + - = 8 ;

  ∙ = ab;

  = =  

Примечание. При вынесении переменной за знак кор­ня необходимо помнить, что это преобразование будет верным только при неотрицательных значениях переменной.

 Если a ≥ 0, то = a.

При внесении переменной под знак корня также следует помнить, что под корень можно вносить лишь положительные числа.

 Если a ≥ 0, то a = .

 Следует сказать, что при преобразовании выражений с корнями можно применять все раннее изученные правила алгебры. В частности умножение одночлена на многочлен, умножение многочленов и формулы сокращенного умножения.

5. Закрепление изученного материала.

     Для закрепления выполним задания №499, 500, 502 – где необходимо вынести множитель за знак корня; и вносить множитель под знак корня.

Релаксация.

Почти 90% всей информации человек воспринимает глазами. Если устают глаза, снижается наше внимание и активность. Давайте перед следующей задачей дадим отдых глазам и себе.

Чтоб глаза твои зоркие были,

Чтоб в очках тебе не ходить,

Эти лёгкие движенья

Предлагаю повторить.

Вдаль посмотри и под ноги,

Вправо, влево побыстрей.

Удивимся, что такое?

И закроем их скорей.

А теперь по кругу быстро,

Словно стрелочка часов,

Проведём глазами дружно,

Ну, а дальше будь здоров!

  №504 упрощаем выражения путем приведения подобных слагаемых.

6. Итоги урока. Рефлексия

Закончите свои высказывания предложением:   

 Я сегодня на уроке  узнал………

                                   научился…….

                                    могу…….

   Подведение итогов урока  и оценивание достигнутых результатов.  

5.Домашнее задание  § 2. П. 16,  № 501, 503, 505.