Урок алгебри у 9 класі "Графічний метод розв'язування систем рівнянь з двома змінними"

Урок алгебри з теми «Графічний метод розв’язування систем рівнянь з двома змінними», проведений в 9 – А класі Прилуцької гімназії № 1 ім. Георгія Вороного Прилуцької міської ради Чернігівської області. Учитель Минка Галина Володимирівна

Тема уроку. Графічний метод розв’язування систем рівнянь з двома змінними

Мета уроку. Повторити: графічний метод розв’язування систем лінійних рівнянь з однією змінною. Навчити розв’язувати системи рівнянь з двома змінними графічним методом, в тому числі і з застосуванням ППЗ «Динамічна математика».

Розвивати: уміння спостерігати і порівнювати; пізнавальну активність; темп записів і рахунку.

Виховувати: навички дослідницького характеру; логічне мислення.

Тип уроку.    Засвоєння нових знань, навичок, вмінь.

Обладнання. Підручник «Алгебра 9, для класів з поглибленим вивченням математики», автори Мерзляк А.Г., Полонський В.Б., Якір М.С., комп’ютери, мультимедійний проектор, додатковий монітор, програми Advanced Grapher, GeoGebra, My Test, тест «Графік рівняння з двома змінними», картки з завданнями.

Хід уроку

І. Перші 30 хвилин.

1. Перевірка домашнього завдання:

     а)  робота за картками (два учні за додатковими комп’ютерами, їх роботу продемонструвати на додатковому моніторі):

  б)  колективне виконання вправи:

Побудувати графік рівняння |х| + |2у| = 4.

2. Актуалізація опорних знань учнів:

а) повторити основні методи розв’язування систем лінійних рівнянь з двома невідомими;

б) алгоритм розв’язування системи лінійних рівнянь графічним способом;

в) два учні за додатковими комп’ютерами проходять тестування у програмі My Test.

3. Мотивація навчальної діяльності.

Постановка проблемного питання: як розв’язати системи нелінійних рівнянь.

Розв’язати системи рівнянь:

а) 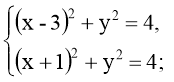      б)  

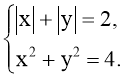
4. Повідомлення теми, мети, завдань уроку:
   •      навчитися розв’язувати системи, у яких обидва рівняння – нелінійні;
   •      навчитися розв’язувати системи рівнянь з двома змінними графічним способом.

5. Приклади розв’язування систем рівнянь.

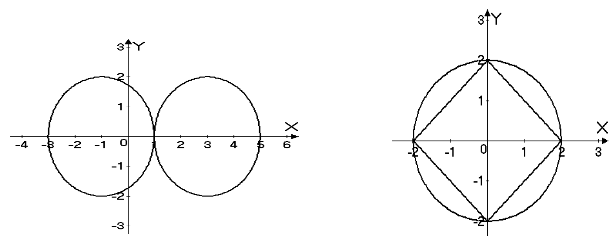Розв’язуються з використанням програми Advanced Grapher системи, які були запропоновані в п. 3.

Відповідь: {(1; 0)}    Відповідь: {(2; 0); (-2; 0); (0; -2); (0; 2)}

6. Розв’язати графічно системи рівнянь в зошитах та на дошці (систему координат взяти з GeoGebra):

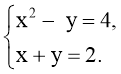
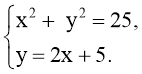
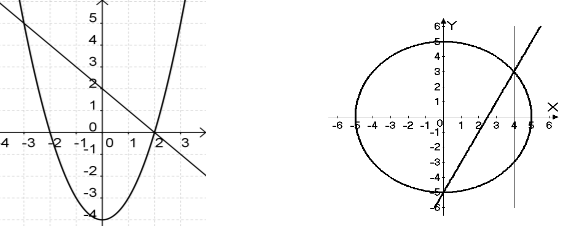
Відповідь: {(–3; 5); (2; 0)}        Відповідь: {(4; 3); (0; - 5)}

7. Застосування графічного способу до дослідження кількості розв’язків систем рівнянь (використовуємо програму GeoGebra):

• вправа 16.3 (1, 2, 6) – колективно;
• вправа 16.3 (7, 8) – на додаткових комп’ютерах.

8. Підсумок перших 30 хвилин.
   • Які існують методи розв’язування систем рівнянь?
   • В яких випадках краще використовувати графічний метод?
   • Які є алгоритми розв’язування систем?

ІІ. Другі 30 хвилин. Вироблення навичок і вмінь розв’язування систем.

1. Розв’язати графічно системи рівнянь:

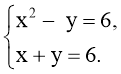
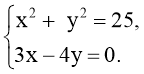
Відповідь: {(–4; 10); (3; 3)}        Відповідь: {(4; 3); (- 4; - 3)}

2. Розв’язати системи рівнянь зручним способом:    

а) 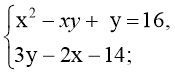     б)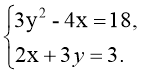

Відповідь: {(4; 6); (8,5; 7,5)}                  Відповідь: {(–1,5; 2); (7,5;–4)}

в) 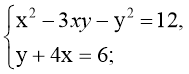   г)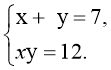

Відповідь: {(2; –2); (8; –26)}   Відповідь: {(4; 3); (3; 4)}

3. Підсумок других 30 хвилин:   
   • які методи розв’язування систем ми використовували?
   • скільки розв’язків мають системи в залежності від степеня рівняння?

ІІІ. Треті 30 хвилин. Повторення і вивчення питань про системи рівнянь з параметрами.

1.                 Розв’язати систему всіма способами:  

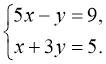
 Відповідь: {(2; 1)}.

2.                 Вивчити способи дослідження системи двох рівнянь з двома невідомими.

Система 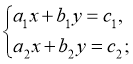містить два лінійних рівняння, графіком яких є прямі. Можуть бути наступні випадки розміщення прямих: перетинаються, паралельні і співпадають. У кожному з них система має різну кількість розв’язків: один, жодного, безліч. Отже, система має один розв’язок, якщо ; система не має розв’язків, якщо ; система має безліч розв’язків, якщо .

3. Дослідити систему:   

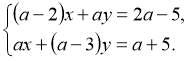
Розв’язання.

1) Система має 1 розв’язок, якщо ;

а² – 5а + 6 ≠ а²;    а ≠ .

2) Система не має розв’язків, якщо . Тоді маємо:

      .

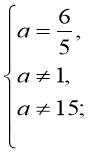
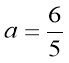3) Система має безліч розв’язків, якщо . Тоді маємо:

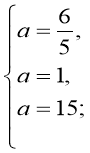   a є ø .

6. Підсумок уроку:

• що називається системою рівнянь з двома невідомими?
• що є розв’язком системи рівнянь з двома невідомими?
• які існують випадки дослідження системи двох лінійних рівнянь з двома невідомими?

Д/З.   Вивчити п. 16

 Виконати вправи 16.4, 16.7 (с. 158).