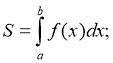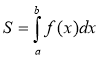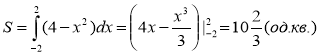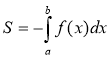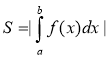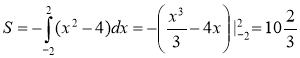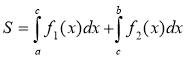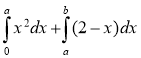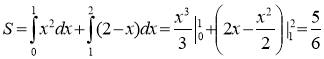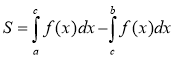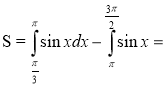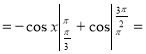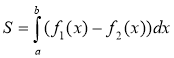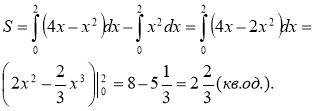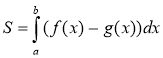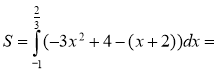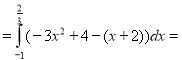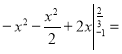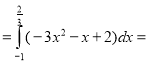УРОК (Алгебра 11 клас) "Обчислення площ плоских фігур"

УРОК  (Алгебра 11 клас)

Обчислення площ плоских фігур.

 

Мета уроку: працювати над засвоєнням учнями поняття плоскої фігури, сформувати вміння виконувати рисунки плоских фігур;

знаходити межі інтегрування у формулі для обчислення площі

фігури, застосовувати інтеграл до знаходження площ плоских фігур;

розвивати логічне мислення, пам’ять, увагу, математичну грамотність; виховувати акуратність, наполегливість, інтерес до

вивчення математики.

Тип уроку: засвоєння нових знань і вмінь

 

Перевірка домашнього завдання.

Учні проводять перехресну перевірку домашнього завдання.

Вибіркові завдання троє учнів виконують біля дошки

 

Актуалізація опорних знань.

 

Завдання «Розпізнавач».

 

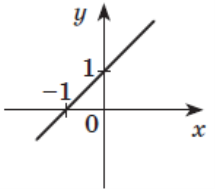
Установіть відповідність між функціями (А–Ж) та ескізами їх

графіків (1–6).                                                  

 

 

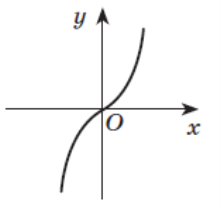
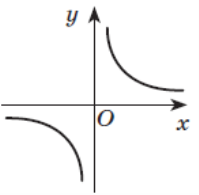
1                           2                          А  у = 1 - х²

                                                   

                                               

                                                        Б  у = х  + 1

                                                                     

 

                                                                                       

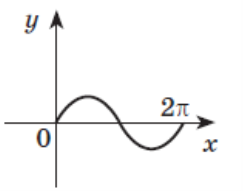                                                                                            В  у = х³

 

 

3                                 4                                

                                                                       Г  y = sinx

 

                                                                             

                                                                                   

                                                                                      Д   y =

 

 

 

 

5                           6                             Е    y =

 

 

                                                                                     Ж   y =

                                                         

                                                                        

 

Виконання усних вправ

 

1. Знайдіть проміжки знакосталості функції:                            

    1) f (x) = x +5; 2) f (x) = (x −1)³ ; 3) f (x) = x² + 3x; 4) f (x) = 4x − x² .  

 

2.   Графік якої з функцій -  f₁(x) чи f₂(x) розташований вище на

     відрізку [a;b], якщо:                                                                

    

     а) f_{1 (}x) = (х-2)²_, ) f_{2 (}x)=х, а=1, b = 4;

     б) f_{1 (}x) = х², f_{2 (}x)=, а=0, b =1?

 

3.  Укажіть правильний вираз для обчислення площі фігури,

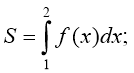
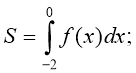
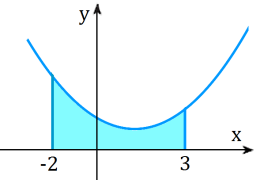    зображеної на рисунку.                                                            

 

    а)                        б)

 

 

 

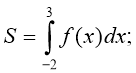
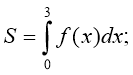
в)                         г) 

 

 

4. Знайдіть площу фігури, обмежену лініями y = x² +1, x = −3,  x = 3 та віссю абсцис.                                                                                  

  

Формулювання мети і завдань уроку.

 

Для створення відповідної мотивації пропонуємо учням розв’язати завдання.

 

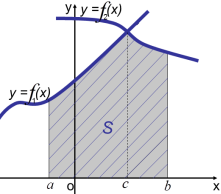
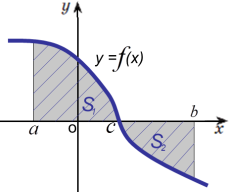
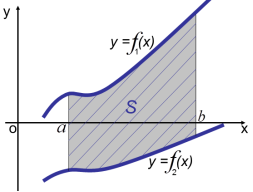
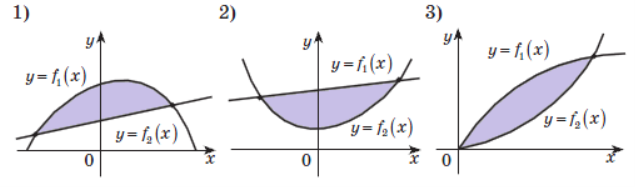Завдання.  Обчисліть площу фігури, зображеної на рисунку:

 

 

 

 

 

 

 

 

 

 

Обговорюючи види фігур, зображених на рисунках, учні мають

усвідомити, що жодна з них не є криволінійною трапецією.

Проте площі цих фігур можуть бути виражені як різниці площ деяких

криволінійних трапецій.

Таким чином формулюємо завдання: навчитися обчислювати площі фігур, що можуть бути виражені через суму або різницю

скінченної кількості криволінійних трапецій.

У цих випадках будемо використовувати такі властивості площ:

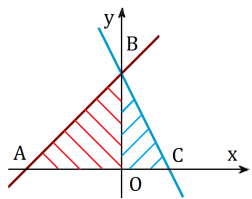1. Якщо фігуру розбити на скінченне число фігур, які не мають спільних внутрішніх точок, то її площа дорівнює сумі площ цих фігур;

 

 

 

 

 

 

 

 

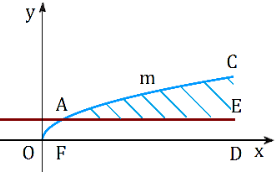
        S_ABC =  S_AOB + S_BOC                         S_AmCE =  S_FAmCD – S_FAED

2. Площа фігури зберігається при переміщенні, зокрема, при паралельному перенесенні і перетворенні симетрії відносно точки і прямої.

 

Засвоєння нових знань.

 

Опорний конспект №6

 

Обчислення площ плоских фігур	Приклади
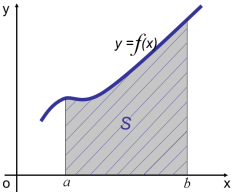
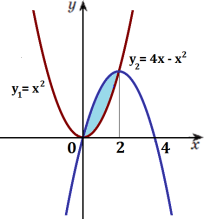
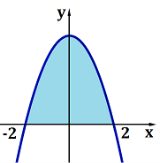
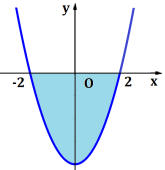
1. Якщо функція f (x) неперервна і невід’ємна на відрізку [a;b], то площу фігури, обмеженої графіком цієї функції та прямими x = a і x = b, обчислюють за формулою	Обчисліть площу фігури, обмеженої графіком функції y = 4 − x2 та віссю абсцис.     Розв’язання: Графік функції y = 4 − x2 перетинає вісь Ох у точках з абсцисами  −2  і  2. Функція y = 4 − x2 неперервна і невід’ємна на відрізку [−2;2].

 

 

                                                                                          

2.Якщо неперервна функція f (x)≤ 0 на відрізку [a;b], то площу відповідної криволінійної трапеції обчислюють за формулою	Обчисліть площу фігури, обмеженої графіком функції  y = x2 − 4 і віссю  абсцис. Розв’язання: Графік функції y = x2 − 4 перетинає вісь Ох у точках з абсцисами  −2 і 2. Функція y = x2 − 4 неперервна і від’ємна на відрізку [−2;2].
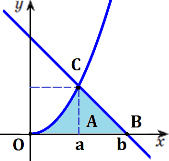
3.	Обчисліть площу фігури, обмеженої лініями у=x2, у=2-х і віссю ох. Розв’язання:   S=                             Знаходимо межі інтегрування:    у=2-х            у=x2    у=0               у=2-х     х=2             х=1, х=-2;  а=хА=1,   b=хВ=2.
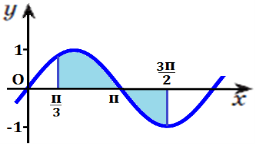
4. Якщо функція неперервна на відрізку [a;b] і набуває на цьому відрізку  як додатних, так і від’ємних значень, то	Обчисліть площу фігури, обмеженою синусоїдою у=sinx та віссю ох, якщо  ≤х≤. Розв’язання:

5. Площу фігури, обмеженої графіками двох непереривних функцій f1(x), f2(x) і двома прямими х=а, х=b, де  f1(x)≥ f2(x) на відрізку [a;b], обчислюють за формулою

Обчисліть площу фігури, обмеже- ної графіками функцій у=х2 і у=4х-х2. Розв’язання: Знайдемо абсциси точок перетину функцій: х2=4х-х2, звідси х1=0, х2=2. На відрізку [0;2] у2≥у1.

 

Формування вмінь.

 

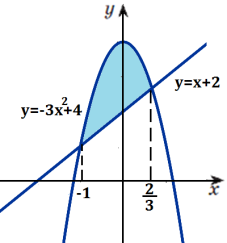
Приклад.  Обчисліть площу фігури, обмеженої лініями

                   у=-3х² +4, у=х+2.

Алгоритм	Розв’язання
1. Зобразити фігуру, площу якої треба знайти. у=f(x), y=g(x)	1. Графіком функції у=-3х2 +4 є парабола, вітки якої направлені вниз, оскільки а=-3<0. (m;n) – координати вершини m=  n=4, (0;4). Точки перетину з осями координат З Ох: у=0   -3х2 +4=0; х2=;  х1=-;  х2=. ()  (). З Оу: х=0   у=4   (0; 4) у=х+2 – графіком є пряма х=0   у=2  (0;2),   х=-2   у=0  (-2;0)
2.Знайти абсциси точок перетину ліній, тобто межі інтегрування, розв’язавши рівняння f(x)=g(x). Корені рівняння є межами інтегрування	2. Знайдемо абсциси точок перетину ліній, тобто межі інтегрування. -3х2+4=х+2, 3х2+х-2=0. х1=-1, х2=,     а=-1, b= – межі інтегрування

3. Обчислити площу фігури, знайшовши інтеграл                                                      якщо f(x)> g(x)

3. у=-3х2 +4 – верхня лінія у=х+2 – нижня лінія                                           =(-)-(1- - 2)=2 (кв. од.)

Розв’язуємо разом

Обчисліть (попередньо виконавши рисунок) площу фігури, обмеженої заданими лінями.

1. а)y = x³, y = 8, x = 1; б) y = x², y = 2x.

2. а) y = 4x − x², y = 4 − x; б) y = x² − 2x + 4, y = 3, x = −1.

3. Обчисліть площу фігури, обмеженої графіком функції y=8x−x²,

дотичною до цієї параболи в її вершині та прямою x = 0.

Робота в парах

Пара, яка першою виконає завдання, записує розв’язання на дошці.

Обчисліть (попередньо виконавши рисунок) площу фігури, обмеженої заданими лінями:

1. а) у=х²-4 і у=0; б) у=, у=2, х=9                                         

 

2. а) y = 2− x³, y = 1, x = −1, x = 1; б) y = x² і прямою y = 2x.          

3. а) у=х² + х - 4 і у = 6-х²;  б) y = 2cosx, y = 1, x = − x = .       

Підбиття підсумків уроку.

 

Укажіть формулу, за допомогою якої можна обчислити площу

фігури:                                                                                             

 

 

 

 

 

 

 

 

          

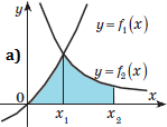
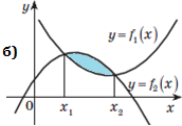
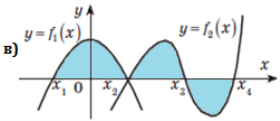
           Домашне завдання.

Вивчити теоретичний матеріал (опорний конспект №6),

підручник А.Г. Мерзляк, Д.А. Номіровський,   В.Б. Полонський,

М.С. Якір  Алгебра  11 класс. Завдання: № 26.11, 26.21

Додатково:  Обчислити площу фігури, обмеженої лініями

                     y = −x² +6x −2,  y = x² −2x + 4.