Урок. Алгебра 9 клас.". Розв'язування систем (та сукупностей) лінійних нерівностей з однією змінною"
Про матеріал
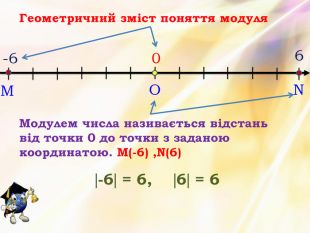
Презентація до уроку алгебри 9 клас. Буде цікавою як для учнів, так і для вчителів. Містить матеріал про сузір`я, астрономію. Є музична фізкульт.хвилинка, тести для перевірки знань, схеми і таблиці.
Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
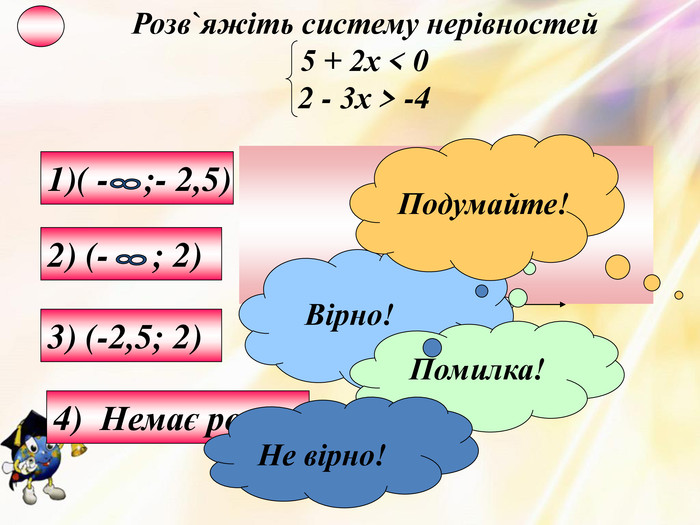
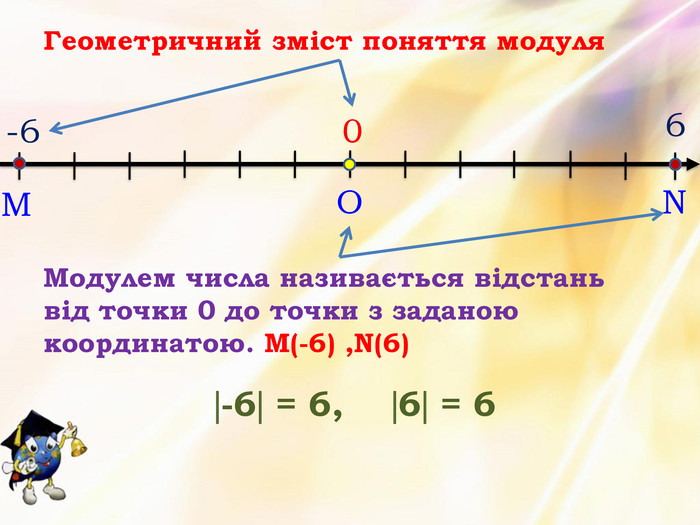
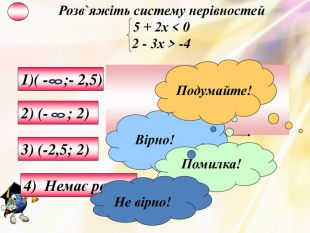
6. Системи лінійних нерівностей з однією змінною Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




![Числові проміжки х>6, х<5, х≥-3, х ≤ -1, х э (6;∞) х э (-∞;5) х э [-3;∞) х э (-∞;-1] Числові проміжки х>6, х<5, х≥-3, х ≤ -1, х э (6;∞) х э (-∞;5) х э [-3;∞) х э (-∞;-1]](/uploads/files/164213/63019/67546_images/4.jpg)
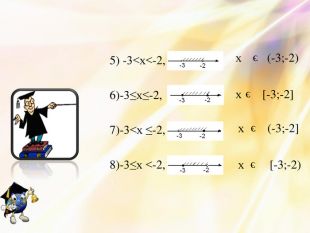
![5) -3<х<-2, 6)-3≤х≤-2, 7)-3<х ≤-2, 8)-3≤х <-2, х э (-3;-2) х э [-3;-2] х э (-3;-2]
х э [-3;-2) 5) -3<х<-2, 6)-3≤х≤-2, 7)-3<х ≤-2, 8)-3≤х <-2, х э (-3;-2) х э [-3;-2] х э (-3;-2]
х э [-3;-2)](/uploads/files/164213/63019/67546_images/5.jpg)