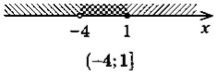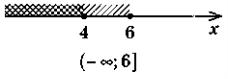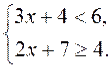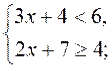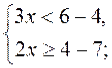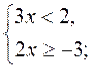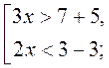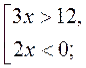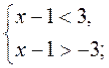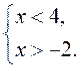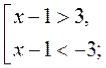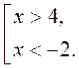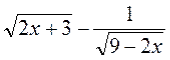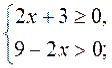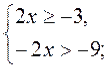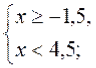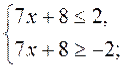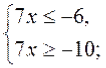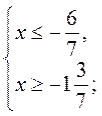Урок. Алгебра 9 клас. " Системи нерівностей"

Урок алгебри в 9 класі. Тема. Розв'язування систем (та сукупностей) лінійних нерівностей з однією змінною

Підготувала вчитель математики Полтавської ЗЗСО №34 Крупка Олена Валентинівна.

 Мета уроку

• навчальна: домогтися закріплення понять система та сукупність, виробити вміння розв’язувати системи та сукупності нерівностей з однією змінною;
• розвивальна: розвивати логічне мислення, алгоритмічну культуру та розумову активність учнів
• виховна: виховувати любов до математики, ініціативу.

 Виробити вміння: виконувати дії відповідно до вивчених схем для розв'язування систем і сукупностей нерівностей з однією змінною. Продовжити роботу з вдосконалення вмінь: відтворювати зміст вивчених понять і алгоритмів; застосовувати їх для розв'язування вправ, що передбачають розв'язування лінійних нерівностей з однією змінною.

Тип уроку: формування та закріплення знань, вироблення вмінь.

Наочність та обладнання: опорний конспект,компютерна презентація, дидактичний матеріал, опорні схеми.

Хід уроку

I. Організаційний етап. Доброго дня, діти!Сьогодні нас з вами очікує мандрівка Всесвітом Математики, тому бажаю вам успіхів, будьте уважними і активними! Вперед до нових знань, перемог і зірок!І памятайте.

Єдиний шлях що веде до знань – діяльність

Б.Шоц

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.  

II. ВИКЛИК (актуалізація знань і вмінь учнів)

Усне опитування. Метод « Гірлянда запитань». Діти працюють в парах, складають розрізане правило і задають до нього питання.

 Розв`язком нерівності з однією змінною називають значення змінної, яке перетворює її в правильну числову нерівність.

Розв`язати нерівність означає знайти всі її розв`язки або довести, що їх не існує.

Якщо нерівність розв`язків не має, то множиною її розв`язків є порожня множина.

Нерівності називають рівносильними, якщо вони мають одну й ту саму множину розв`язків.

Якщо обидві частини нерівності поділити або помножити на одне й те саме від`ємне число і замінити знак нерівності на протилежний, то отримаємо правильну нерівність.

Якщо обидві частини нерівності помножити або поділити на одне й те саме додатнє число, то отримаємо правильну нерівність.

Строгими називають нерівності, що містять знаки ˂ ;˃ .

Нестрогими називають нерівності, що містять знаки ≤ ;≥ .

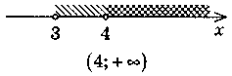
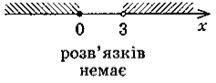
2.  Завдання: за малюнком визначити правильність проміжка відповідному малюнку Діти коментують з місця.

3.Завдання на відповідність( самостійно)

1. Встановити відповідність між лінійною нерівністю та її розв’язком

1) х + 3 > 5;                                  А) x є (-∞;-1)

2) 0х < 7;                                      Б) х є (-∞;+∞)

3) -3х > 3;                                     В) розв’язків немає

4) 0х > 7                                        Г) х є (2; +∞)                       

[Відповіді: 1Г, 2Б; 3А; 4В]

Діти підраховують кількість зароблених зірочок.(7хв.)

ІІ. Реалізація (осмислення)

А зараз , діти, задача.

З різних станцій з однаковою швидкістю стартувало дві ракети. Перша ракета пролетіла за 0,5 год. Відстань, більшу за 130000 км. Друга ракета за 0,3 год. Пролетіла відстань, меншу за 90000 км. Знайти можливе значення швидкості цих ракет.

Нехай швидкість ракет –X км/год., тоді складаємо дві нерівності :

0,5Х > 130000                  Х > 260000

0,3Х < 90000           Х <300000      Відповідь: швидкість ракети може приймати значення від 260000км/ год до 300000км/ год.

У мaтемaтиці іноді виникaє необхідність визнaчити спільні розв’язки декількох нерівностей. Тоді говорять, що необхідно розв’язaти систему нерівностей.

Системa нерівностей з однією змінною це дві aбо більше нерівності, об’єднaні для пошуку спільних розв’язків. У зaпису системи їх об’єднують злівa фігурною дужкою.

Розв’язaти систему нерівностей ознaчaє знaйти множину її розв’язків aбо довести, що їх не існує.

Розв’язок системи нерівностей ― це знaчення змінної, яке зaдовольняє кожну нерівність дaної системи.

Щоб розв’язaти систему нерівностей, необхідно розв’язaти окремо кожну нерівність, після чого знaйти переріз одержaних розв’язків, що й буде розв’язком системи нерівностей.

Нaприклaд : (слайди)

Діти розв`язують найпростіші системи, заздалегідь записані на дошці ланцюжком (по одному з парти). Умови закриті картинками зоряного неба або висловами про математику. Числові прямі теж заготовлені на дошці.

1. Розв’язaти систему нерівностей

	х > 1,
	х < 3.

Перерізом множин розв’язків цих нерівностей буде проміжок (1; 3).

2. Розв’язати систему нерівностей

	х > 1,
	х > 3.

Перерізом множин розв’язків цих нерівностей буде проміжок (3; +∞).

3. Розв’язaти систему нерівностей

	х < 1,
	х > 3.

Перерізом множин розв’язків цих нерівностей буде порожня множина Отже, нерівність розв’язків не мaє.

   2.   Розв'яжіть систему нерівностей:

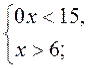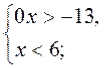4)            5)       6) 

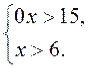
Фізкультхвилинка

Щоб визначити назву сузіря, треба розвязати ці системи нерівностей.

Завдання на слайдах

Потім сукупність двох нерівностей , розвяжемо її разом.  Робимо висновок. Сукупність пишуть за допомогою квадратної дужки  і розвязком сукупності є не переріз, а обєднання проміжків – розвязків нерівностей.  

« Те, що ми знаємо- обмежене, а те, чого ми не знаємо- нескінченне…» Лаплас

 

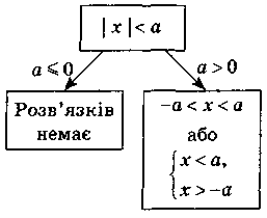
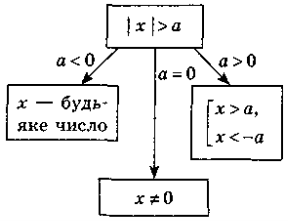
А як застосовуються системи і сукупності нерівностей? Одне із застосувань - нерівності , що містять знак модуля. Давайте пригадаємо означення модуля, яка його геометрична інтерпретація?

Викладення питання про розв'язування найпростіших нерівностей з модулем ведеться традиційно та ґрунтується на геометричному змісті модуля (модуль числа — це відстань від початку відліку на координатній прямій до даної точки). Діти працюють з текстом, де опрацьовують алгоритм розв’язування нерівностей з модулем. Після чого розв’язують найпростіші нерівності з модулем біля дошки.

.   Кожну з нерівностей замініть рівносильною системою або сукупністю нерівностей:

1) |x| > 3;          

2) |x| < 3;          

3) |х – 2 | > 2;    

4) |x – 3| < 1.

ІІІ Рефлексія. Підсумок уроку.

2.   На рисунках позначено множини розв'язків нерівностей системи. Чи є правильним запис множини розв'язків системи?

 

1)		2)
3)		4)

 

Контрольні запитання

1. Що означає «розв'язати систему нерівностей»? Опишіть алгоритм (дії, які треба виконати), щоб отримати розв'язок системи нерівностей. Діти заповнюють пропущені слова в картках- алгоритмах розвязування системи нерівностей та їх сукупностей. Метод Гронування.

Контроль і оцінювання знань учнів (картка оцінювання) самооцінка .Діти підраховують кількість зароблених зірочок і виставляють собі оцінку.

 

VIII.    Домашнє завдання

1.   Вивчити алгоритми виконання дій, складених та опрацьованих на уроці.

2.   Розв'язати завдання на формування навичок використання вивчених алгоритмів.

3.   Повторити означення та геометричний зміст модуля числа.

Є люди,як зорі. Вони згасають,

а світло,яке вони дали,ще довго мандрує всесвітами наших

душ.      В.Сухомлинський

Опорні схеми:



Основні кроки розв'язування системи нерівностей з однією змінною

1. Розв'язуємо кожну нерівність системи. 2. Зображуємо множину розв'язків кожної нерівності на одній координатній прямій. 3. Знаходимо переріз числових проміжків, записуємо відповідь.

Приклад. Розв'яжемо систему нерівностей  Розв'язання     (див. рисунок).  Відповідь: х  .

Основні кроки розв'язування сукупності нерівностей з однією змінною 1. Розв'язуємо кожну нерівність сукупності. 2. Зображуємо множину розв'язків кожної нерівності на одній координатній прямій. 3. Знаходимо об'єднання числових проміжків, записуємо відповідь.

Приклад. Знайдемо розв'язок сукупності нерівностей

Розв'язання     (див. рисунок).

Відповідь: x  (-∞; 0)  (4; +∞).

 

Найпростіші нерівності з модулем
Наприклад: |x – 1| < 3;   x  (-2; 4).	Наприклад: |x – 1| > 3;   x  (-∞; -2)  (4; +∞).
Приклад 1. Визначимо, при яких значеннях змінної має зміст вираз . Розв'язання
Вираз  має зміст, коли підкореневі вирази невід'ємні і знаменник не дорівнює 0, тобто виконується система:
х є [-1,5; 4,5).
Відповідь: [-1,5; 4,5).
Приклад 2. Розв'яжемо нерівність | 7х + 8 | < 2.
Розв'язання
Дана нерівність рівносильна системі:
. Відповідь: .