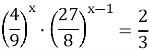Урок алгебри, 11 клас. Готуємося до ЗНО. "Розв'язування показникових рівнянь, нерівностей та їх систем"

Про матеріал

Конспект уроку "Розв'язування показникових рівнянь, нерівностей та їх систем " пропонує  розвивати розумову діяльність, логічне мислення, культуру математичної мови, вміння застосовувати набуті знання до розв’язування вправ;  виховувати самостійність, відповідальність, вмiння виражати i вiдстоювати свою думку, доброзичливість, уміння самоорганізуватись, увагу, почуття гордості за виконану роботу;

Перегляд файлу

Урок алгебри ,

11 клас

ГОТУЄМОСЯ ДО ЗНО

Тема уроку: Розв’язування показникових рівнянь, нерівностей та їx систем

Мета уроку:

виявити глибину учнівських знань, перевірити якість та міцність засвоєння матеріалу, сформованості вмінь і навичок до ЗНО;
розвивати розумову діяльність, логічне мислення, культуру математичної мови, вміння застосовувати набуті знання до розв’язування вправ;
виховувати самостійність, відповідальність, вмiння виражати i вiдстоювати свою думку, доброзичливість, уміння самоорганізуватись, увагу, почуття гордості за виконану роботу;
намагатися скласти ситуацію успіху для кожного учня;
засобами IКТ створити умови для пiдвищення iнтересу до вивчення математики.

Тип уроку: перевірка та оцінювання знань, умінь і навичок.

Обладнання: мультимедійна презентація, рівневі завдання, роздавальний матеріал, для роботи в групах та самостiйноiї роботи.

Епіграф уроку: «Багато чого з математики не залишається в памяті, але коли розумієш її, тоді легко при нагоді згадати призабуте».

М. В. Остроградський

ХІД УРОКУ

І. Організація класу. Створення емоційного настрою.

Учитель. Доброго дня, я рада всіх вас бачити сьогодні. І сподіваюсь, що ви теж прийшли на урок із гарним настроєм. Мені дуже хотілося, щоб слово УРОК викликало у вас тільки такі асоціації як успіх, радість, обдарованість і кмітливість.

ІІ. Формулювання теми, мети і завдань уроку

Досягти успіху можна тільки тоді, коли визначено мету і завдання , які кожен ставить перед собою.

Тема сьогоднішнього уроку це: розв’язування показникових рівнянь, їх систем та нерівностей. (слайд 3)

Епіграфом до уроку я взяла слова видатного українського математика, нашого земляка, про якого ви неодноразово чули, Михайло Васильович Остроградський:

«Багато чого з математики не залишається в памяті, але коли розумієш її, тоді легко при нагоді згадати призабуте.»(слайд 4)

Сьогодні у нас з вами не зовсім звичайний урок. Це урок – повторення, узагальнення,і систематизації знань, умінь і навичок. А основна мета нашої роботи полягає в тому, що ми перевіримо міцність засвоєння матеріалу,та вашу готовнiсть до проведення ЗНО.(слайд 5)

Розвиватимемо логічне мислення, пам’ять, вміння застосовувати здобуті знання до розв’язування вправ, а також виховуватимемо правила роботи в групах та культуру поведінки під час суперечок, намагатимемося скласти ситуацію успіху для кожного учня .

Тож не забуваймо, що успіх приходить до тих, хто мислить категоріями успіху.

ІІІ. Перевірка домашнього завдання

Готуємося до ЗНО

Дорогі діти! Мені дуже цікаво, з яким настроєм ви прийшли на урок математики. Тож я пропоную вам усміхнутися, підготувати зошити до роботи і нагадати, що під час роботи до успіху веде старанне, охайне, уважне виконання завдань.

На цьому уроці ми будемо розв’язувати показникові рівняння, їх системи, та нерівності. Це одна з основоположних частин алгебри.

Готуючись до ЗНО, ми прагнемо, щоб опанована кiлькiсть iнформацiї утворювала у свiдомостi людини цiлiснiсть. У процесi навчання, який передбачав великий промiжок часу, iнформацiя була розбита на частини. Кожна частина засвоювалася не однаково. Деякi частини були незрозумiлими, деякi частини забулися, тому в майбутньому їм важко дiяти разом.

« Багато чого з математики не залишається в пам’яті, але коли розумієш її, тоді легко при нагоді згадати призабуте»,– так говорив наш земляк, видатний математик, Михайло Васильович Остроградський. Тож і ми зараз пригадаємо призабуте, і маю надію на те, що у вaшій пам'яті все ж таки залишаться знання, уміння і навички по даній темі.

(слайд 6)

Виступ творчої групи:

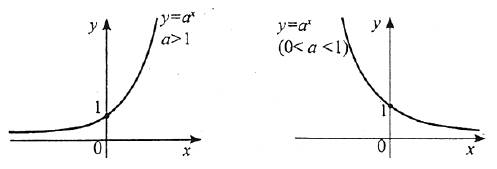
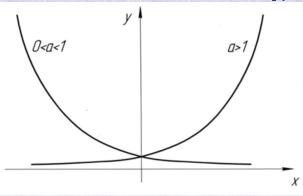
Основнi методи розв’язування показникових рiвнянь	Властивості показникової функції
1. Метод зведення до однiєї основи.	1.D(
2. Метод винесення спiльного множника за дужки.	2.E(
3. Метод введення нової змiнної – тобто зведення рiяння до квадратного вiдносно показникової функцiї.	3. Функцiя загального вигляду.
4. Метод розв’язування однорiдних показникових рiвнянь – тобто потрібно лiву i праву частини рiвняння подiлити на або на	4. Не перiодична, не є нi парною, нi не парною.
5. Графiчний метод розв’язування показникових рiвнянь.	5. Вiсь не перетинає; вiсь ОY перетинає в точцi (0;1).
6. Використання декількох методів.	6. yпри
7. Використання декількох властивостей функції.	7. Вiсь є горизонтальною асимптотою.
	8. Якщо iя є зростаючою, якщо , то функцiя є спадною.
	9. Екстремумiв у функцiї немає.
	10. Власної симетрiї показниковi функцiї не мають, але графiки функцiй та симетричнi вiдносно осi Графік даної функції подано нижче.

$C:\Users\Оля\Desktop\l354.jpg$

$C:\Users\Оля\Desktop\Презентацiя мама папка (4)\1.jpg$

Спробуємо сьогоднi активiзувати якомога бiльше матерiалу по данiй темi.

Запитання для груп: (усно, але з обговоренням в групах) (слайд 10 )


1.Укажiть спосiб розв’язання рiвнянь: а) 5^х = 3, б) 27^х = 9^х -3^х + 2 = 0	1.Укажiть спосiб розв’язання рiвнянь: а)7^х – 7^х-1 = 6, б) 5^х = 8^х, в) 2^3х + 82^х - 62^2х = 0
2.Записати вираз у виглядi степеня з показником х: а) 3^х-2; б) 4^3х+2	2.Записати вираз у виглядi степеня з показником х: а) 5^х+1; б) 3^2х-3
3.Порiвняйте х та у: а) 7^х; б)0,2^х	3.Порiвняйте х та у: а) 4^х; б)0,5^х
4.Якi з наведених функцiй є зростаючими? а) у = ; б)у = ; в) у = г)у = ; д)у =	4.Якi з наведених функцiй є спадаючими? а) у = ; б) у = ; в) у = у = ; д)у =
5.Подайте вираз у виглядi степеня: а) ; б)	5.Подайте вираз у виглядi степеня: а) ; б) 5^х: 7^х
6.Чому дорiвнює х? а)2^х= 1; б)3^х = 9	6.Чому дорiвнює х? а)2^х= 2; б)5^х =

Представники від кожної групи пропонують свої запитання і відповіді.

ІV. Актуалізація опорних знань

Метод: «Мозковий штурм» і вчительська презентація.

Учитель: «Покажи мені – і я запам’ятаю. Дай мені діяти самому – і я навчусь…» говорить давня китайська мудрість.

Подумайте, поспілкуйтеся, спробуйте згадати, якщо потрібно – вигадати, але найголовніше - не мовчіть, а говоріть, які версії прийшли на думку, за потреби можна скористатися підручником, або сторінками міні-конспектів.

Отже, до роботи! (слайд 12-14)

Завдання для груп:

1.Встановити вiдповiднiсть мiж елементами А, Б, В, Г, Д та числами 1, 2, 3, 4

1.Група (слайд 12)

1		А	-2
2	2^х	Б	3
3		В	+
4		Г	-4
		Д	(0;

Вiдповiдi: (слайд 14)

1	В
2	А
3	Г
4	Б

2.Група (слайд 13)

1	А	1; -2
2	Б	2
3	В	5
4	Г
	Д

Вiдповiдi: (слайд 14)

1	В
2	Г
3	А
4	Б

2.Тестовi завдання (слайд 15)

Робота в групах:

Група 1 (слайд 15)

Розв’язати нерiвнiсть (слайд 16)

А	Б	В	Г	Д
			(1;4)

Вiдповiдь: Д

Група 2(слайд 15)

Розв’язати нерiвнiсть (слайд 16)

А	Б	В	Г	Д

Вiдповiдь: Б

(Учні об’єднуються у групи і розпочинають обговорення, діляться своїми думками з групою. Представники від кожної групи пропонують свої запитання і відповіді. (слайд 15, 1 6)

Підбивають підсумки роботи своїх однокласників.

V. Узагальнення і систематизація вивченого матеріалу

Технологія особистісно розвивального навчання: «Коло ідей».

Сьогодні наш урок – це урок ідей. І хоча їх ще не можна назвати великими, пам'ятаймо – велике починається з малого. Разом навчатися не тільки легше і цікавіше, але й значно ефективніше. Тому на цьому етапі уроку будемо працювати під девізом:

Думаємо колективно,

Пропонуємо оперативно,

Сперечаємося доказово –

Це для всіх обов’язково.

Учитель: математик-кораблебудiвельник Олексiй Миколайович Крилов вважав, що рано чи пiзно будь-яка правильна математична iдея знаходить практичне застосування.

Яких навичок, на вашу думку, ви зможете набути на цьому уроцi? (Відповіді учнів: уміння розв'язувати, доводити, захищати думку тощо.) Продовжуємо працювати в группах. У вас буде можливість порадитися один з одним і дійти спільного розв'язання. Проекти захищаєте, відповіді звіряємо з відповідями на екрані мультимедійної дошки.

Розв’язати рiвняння:

Виконати завдання i вказати метод розв’язування показникових рiвнянь :

Приклад 1. = 13(слайд 17)

Розв’язання

(1 + 3 + 3²) = 13;

;

х₁= -1, х₂ = 2.

Вiдповiдь: -1; 2.

Запитання: Якi знання та який метод були використанi пiд час розв’язування цього рiвняння? (винесення спiльного множника за дужки)

Виконати завдання i вказати метод розв’язування показникових рiвнянь :

Приклад 2 (слайд 19)

Розв’язання

= 1,

= – 2, розв’язкiв немає.

Вiдповiдь: 1.

Запитання: Якi знання та який метод були використанi пiд час розв’язування цього рiвняння? (метод зведення показникового рiвняння до квадратного шляхом введення нової змiнної.

Виконати завдання i вказати метод розв’язування показникових рiвнянь :

Приклад 3. х = 0 (слайд 21)

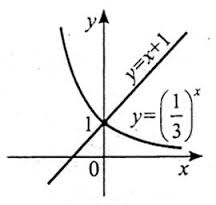
$C:\Users\Оля\Desktop\images (1).jpg$

Вiдповiдь:

Запитання: Якi знання та який метод були використанi пiд час розв’язування цього рiвняння? (графiчний метод розв’язування показникових рiвнянь)

Розв’язати нерiвнiсть: (робота в группах з подальшим поясненням, одного з учнів, біля дошки)

Приклад 1.(слайд 25)

Розв’язання

Подiлимо обидвi частини нерiвностi на

дiстанемо:

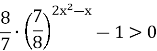
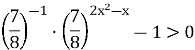
, х_{1 =}1; х₂ =

Вiдповiдь:

Приклад 2. 7+(слайд 24)

Розв’язання

Поділивши ліву і праву частини нерівності на матимемо:

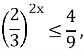
то .

Вiдповiдь:

Розв’язати систему рiвнянь: (один учень розвязує завдання біля дошки з коментуванням)

Приклад 1. (слайд 26)

Розв’язання

Подiлимо перше рiвняння системи на друге, а потiм помножимо:

⟹

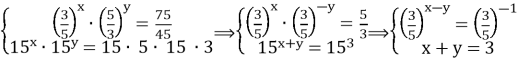Вiдповiдь:

Самостійна робота

Розв’язати нерiвнiсть:

Приклад 1.

Розв’язання

оскiльки 0,7

то

тобто

Вiдповiдь:

Розв’язати систему рiвнянь:

Приклад 2.

Розв’язання

⟹

Вiдповiдь:

VІ. Підсумок уроку

Вітаю вас! Спільними зусиллями ми виконали ряд завдань і виявили себе чудовими знавцями алгебри і початків аналізу. А тепер хочу почути, що вам сподобалося на сьогоднішньому уроці, а, що можна змінити на краще.

Пропоную вам декілька запитань:(слайд 29)

Якою діяльністю ми займалися на уроці?
Як спілкування під час роботи впливало на виконання завдання?
Чи досягли ми очікуваних результатів (цілей)?
Як ви оцінюєте свою роботу?

Продовжити думку:(слайд )

Було цікаво…
Я зрозумів, що…
Я зміг…
Я спробував…
На уроці я працював…
За урок я…
Матеріал уроку був мені…
Своєю роботою на уроці я...

Справді, сьогодні ми багато чого встигли зробити на уроці тож варто оцінити наші зусилля. Пригадаймо ще раз все, що ми зробили сьогодні, чого навчилися і що зрозуміли, як працювали в групі, які ставили запитання.

Поставте собі оцінку за урок.

VІІ. Домашє завдання(слайд 30)

І традиційно одержимо домашнє завдання

Повторити тему: «Розв’язуння показникових рiвнянь, нерiвностей та їх систем» 2, п. 16, 17, 18.

Повторити: «Похiднi елементарних функцiй», «Розв’язуння тригонометричих рiвнянь»

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

4.0

Відповідність темі

5.0

Загальна:

4.7

Всього відгуків: 1

Оцінки та відгуки

Шах Руслана Вікторівна 09.04.2024 в 09:26

Загальна:

4.7

Структурованість

5.0

Оригінальність викладу

4.0

Відповідність темі

5.0

docx

Завантажити

Зберегти на потім

Додав(-ла)

Новицька Олена Анатоліївна

Пов’язані теми

Алгебра, 11 клас, Розробки уроків

Додано

2 лютого 2023

Переглядів

1602

Оцінка розробки

4.7 (1 відгук)