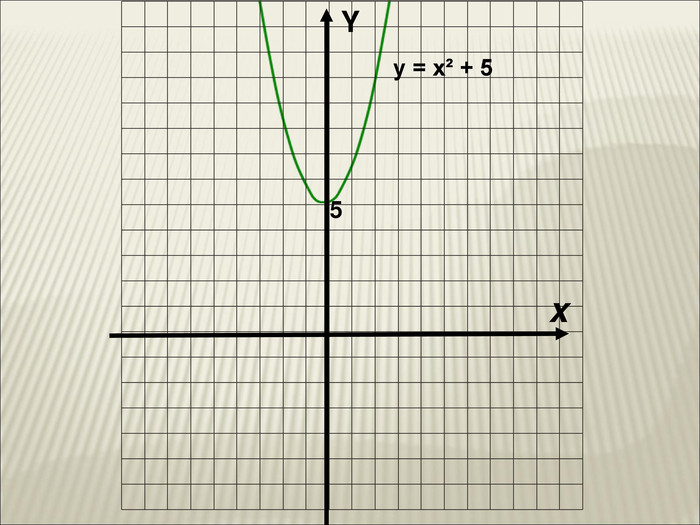
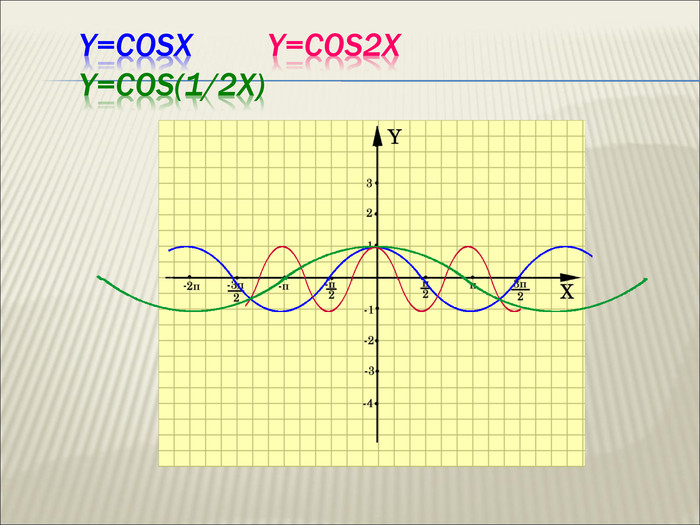
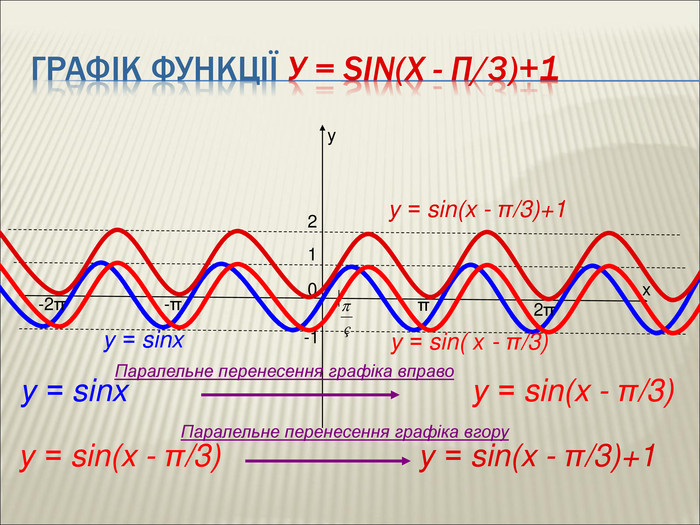
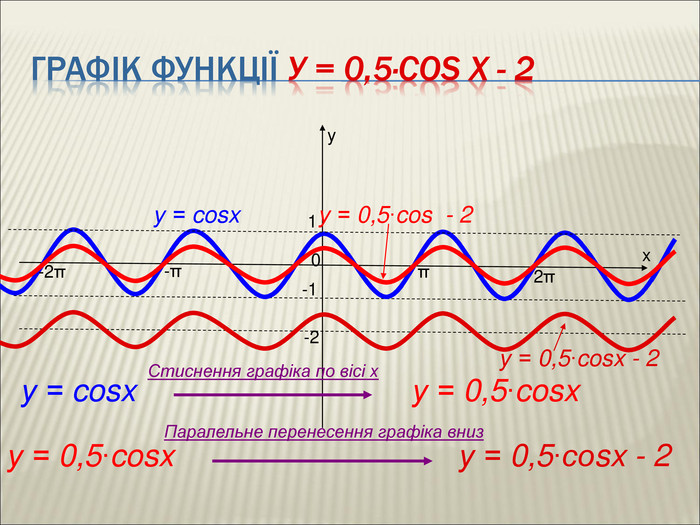
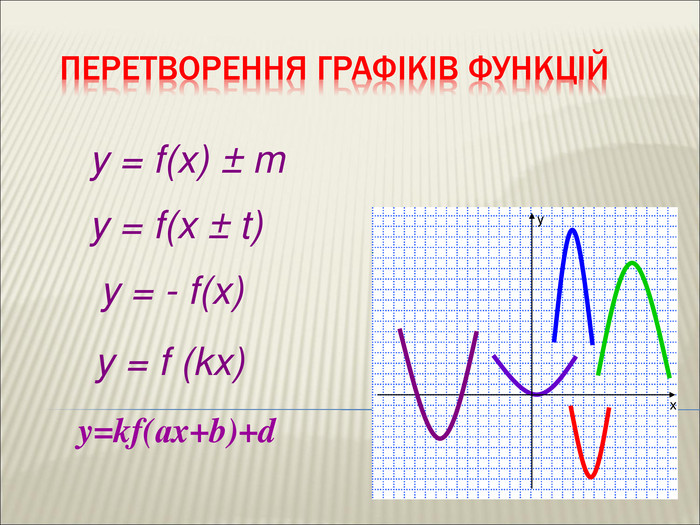
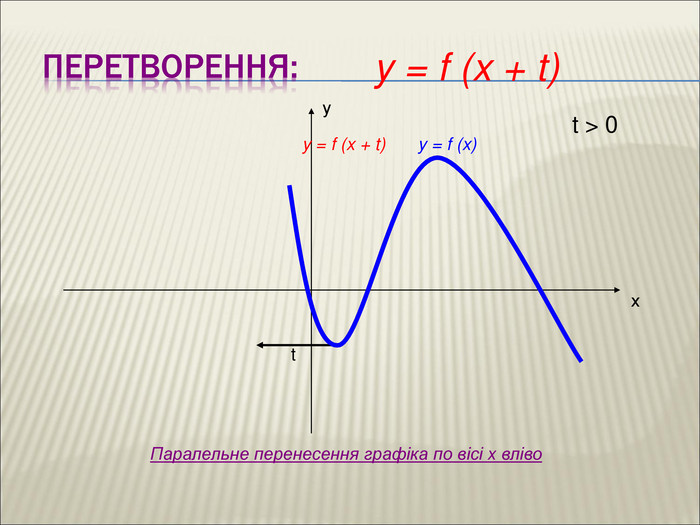
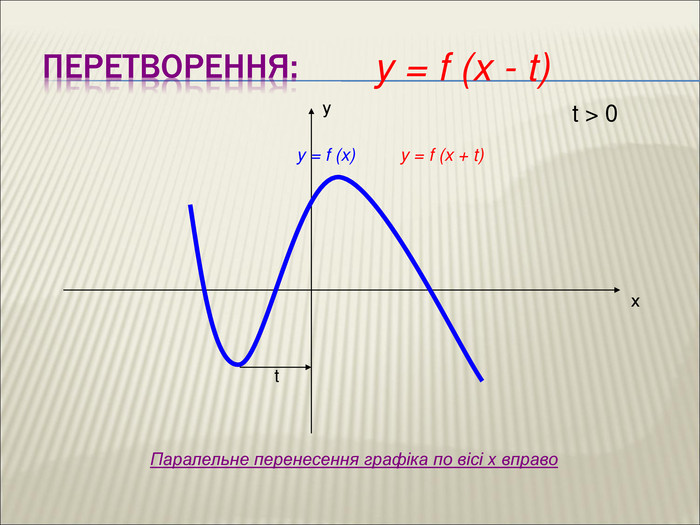
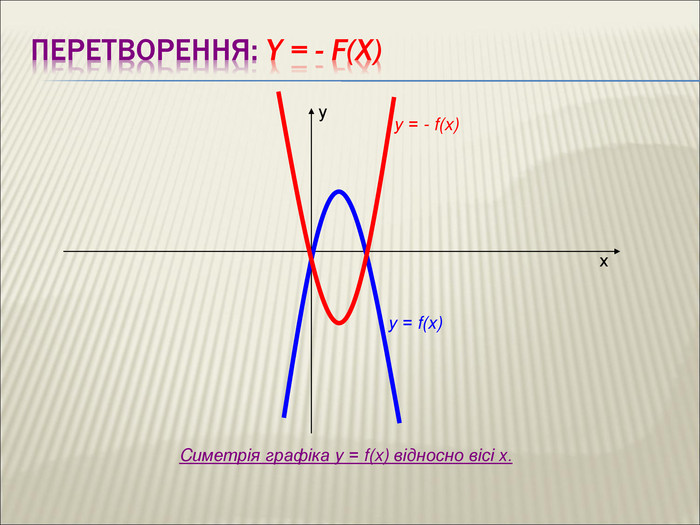
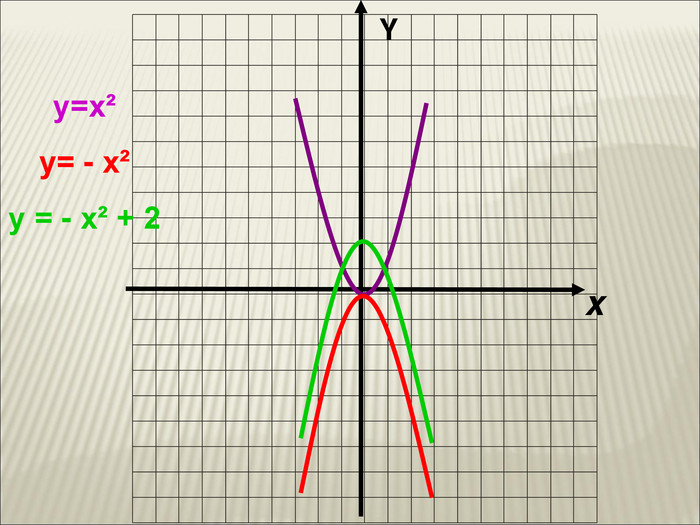
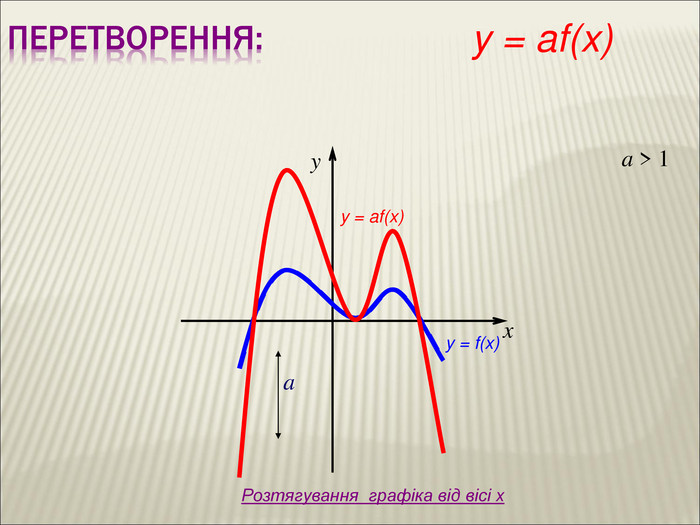
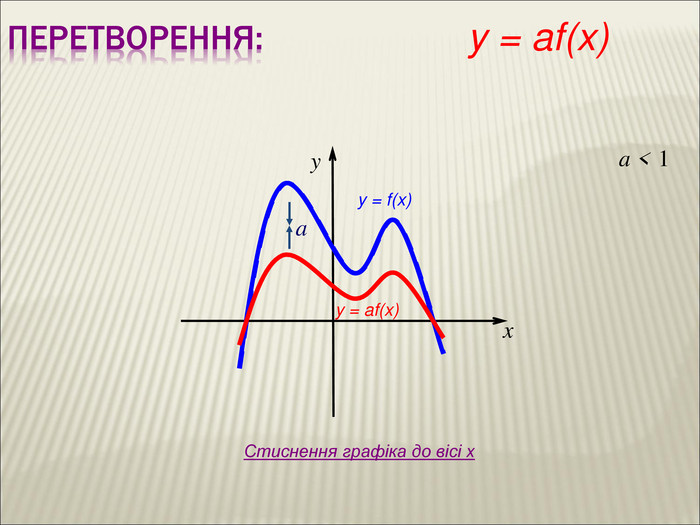
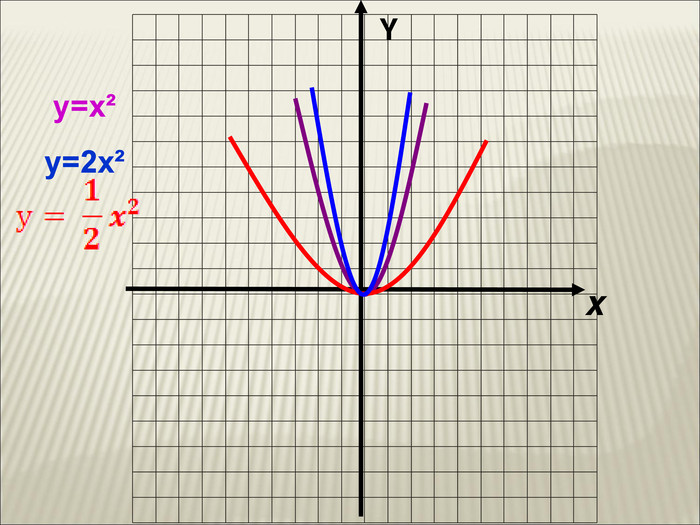
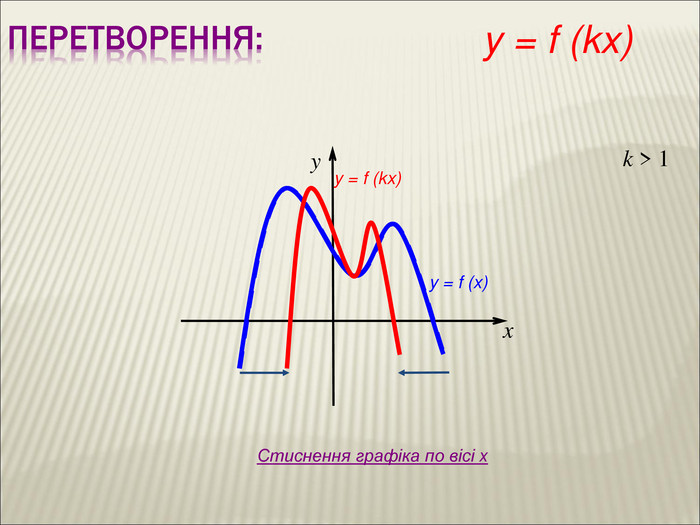
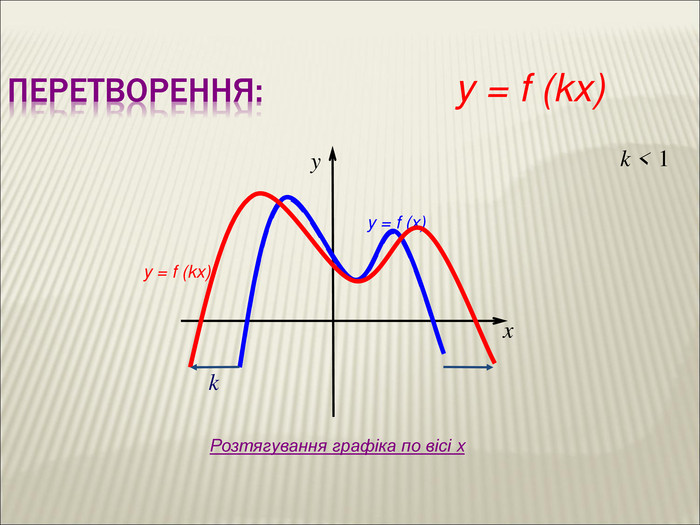
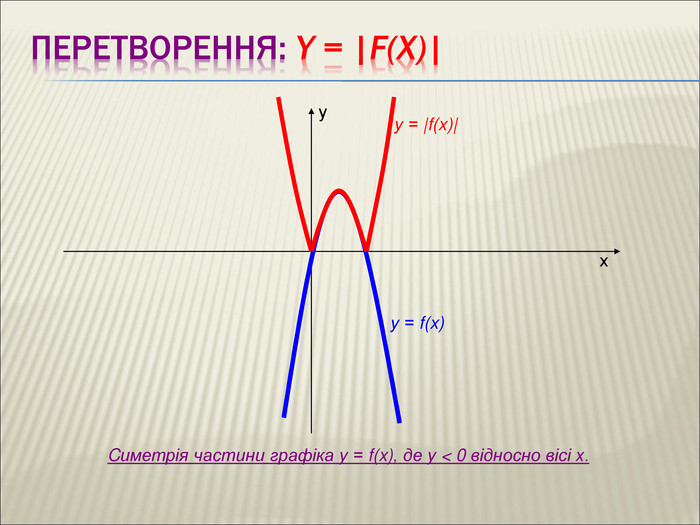
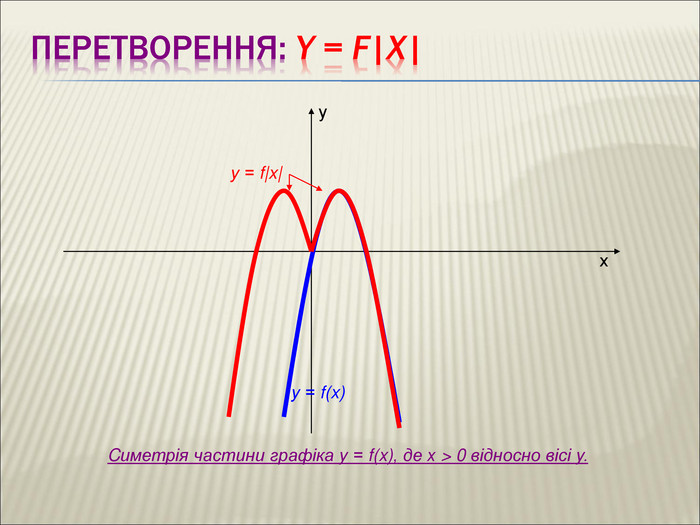
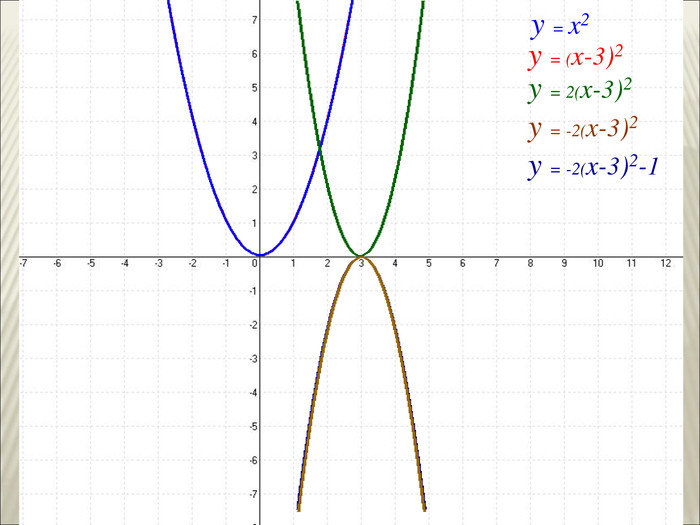
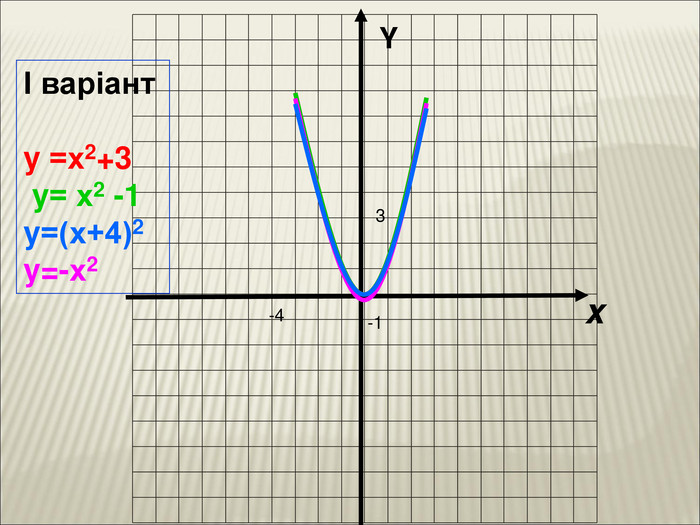
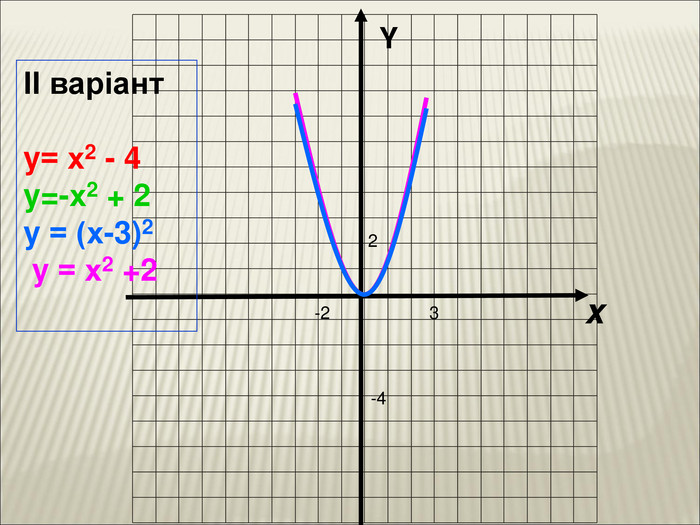
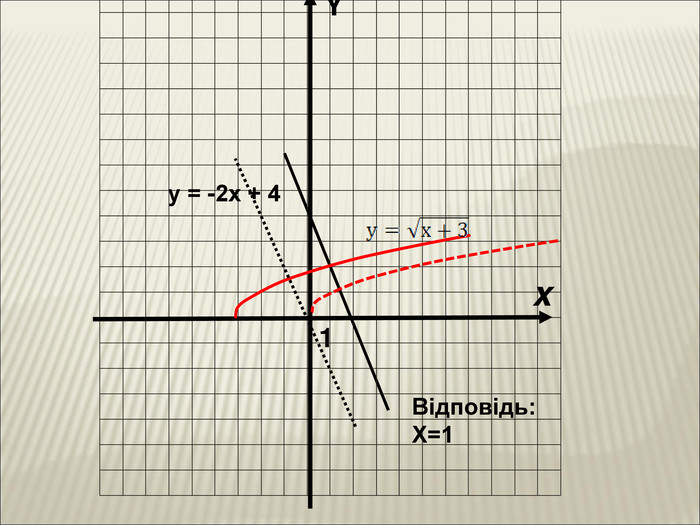
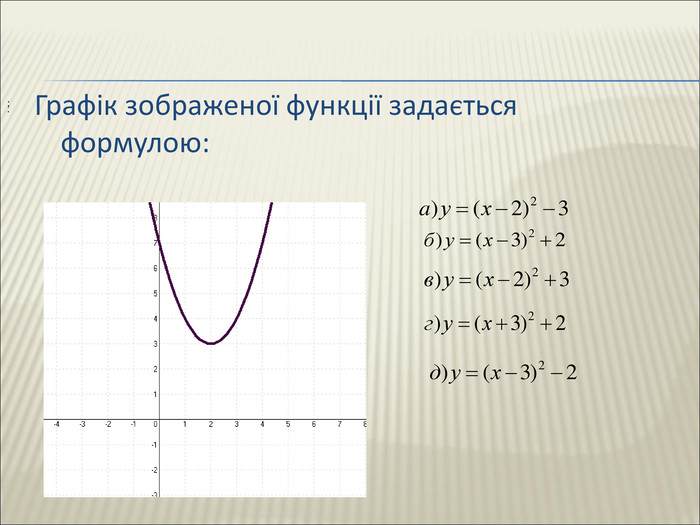
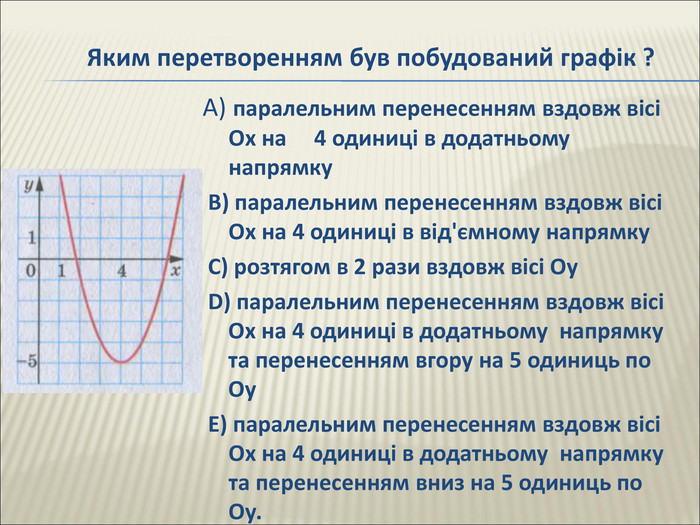
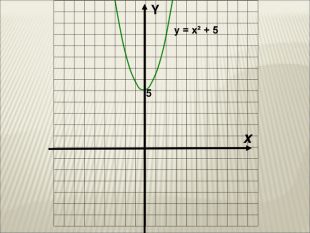
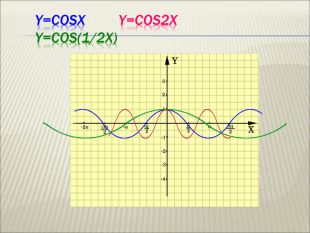
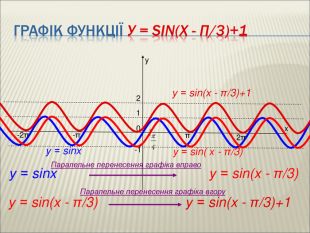
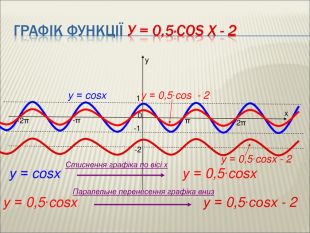
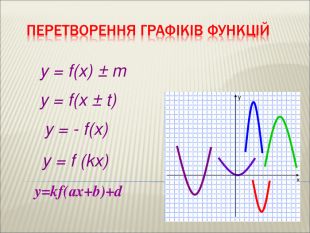
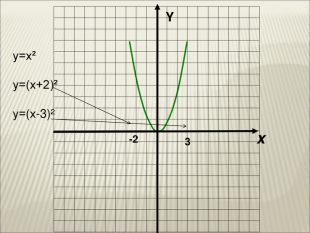
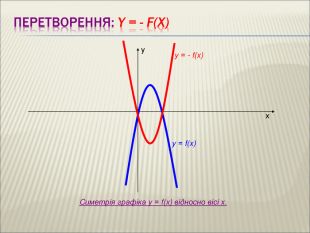
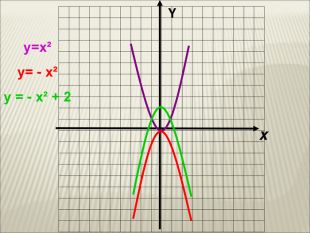
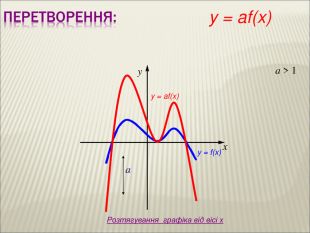
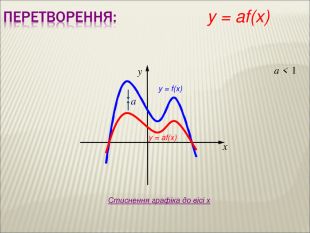
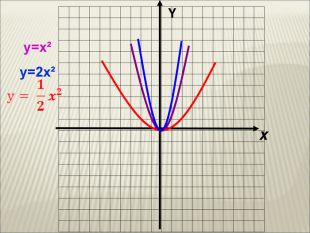
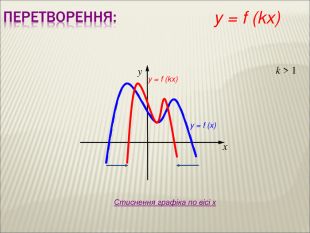
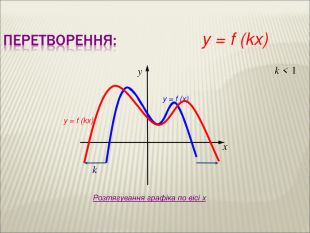
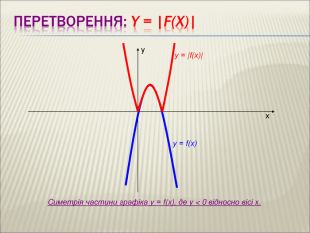
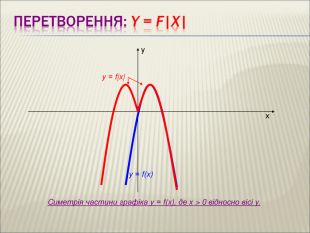
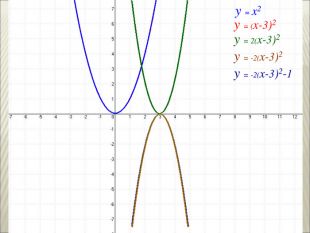
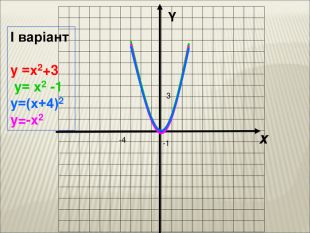
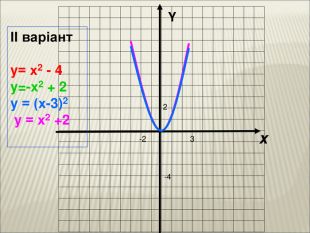
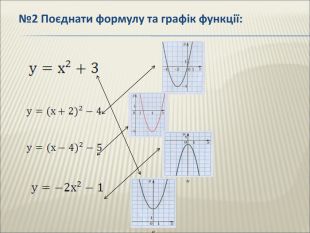
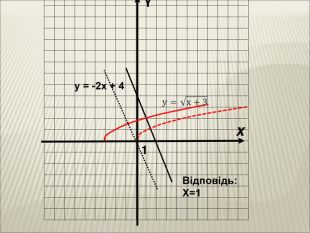
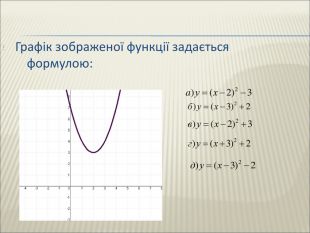
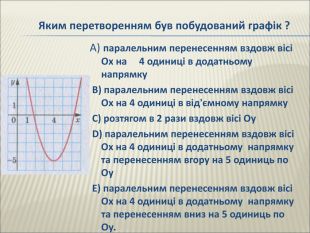
Урок алгебри 9 клас "Перетворення графіків функцій"
Про матеріал
Презентація до уроку алгебри 9 клас "Перетворення графіків функцій"
: Сформувати в учнів розуміння змісту поняття « перетворення графіка функції» , а також поняття про певне перетворення формули, що задає функцію, яке спричиняє перетворення графіка. Сформувати знання в учнів про основні види геометричних перетворень графіків функцій. Сформувати вміння читати графіки функцій( за готовими графіками задавати функцію), а також виконувати побудову графіка, використовуючи певні перетворення. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
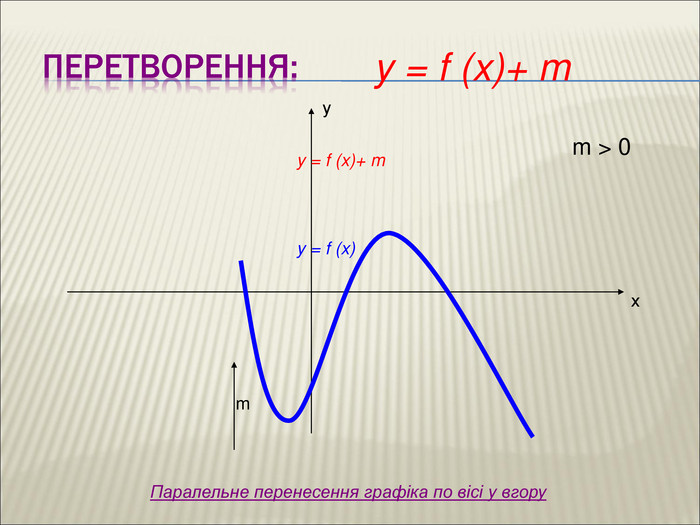
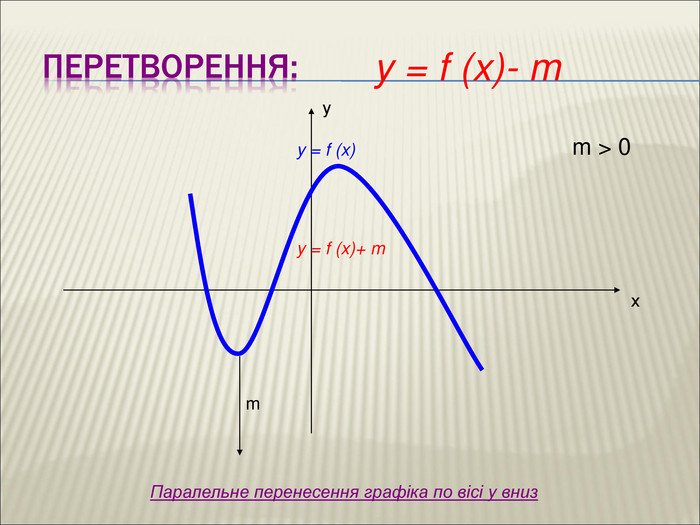
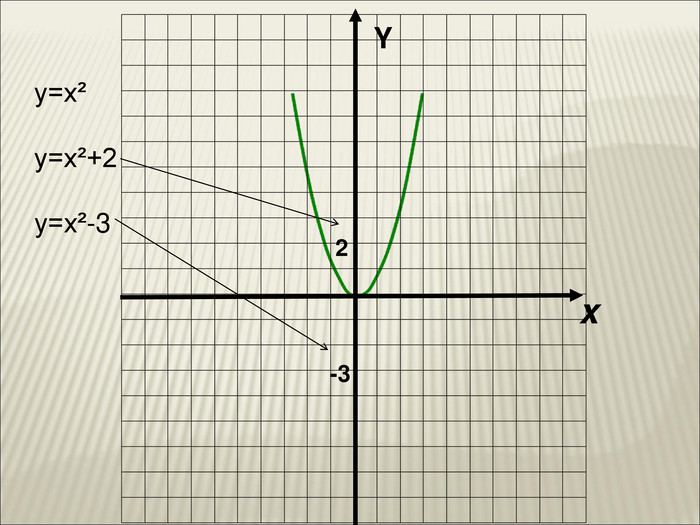
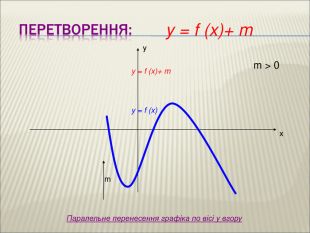
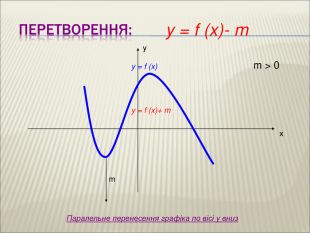
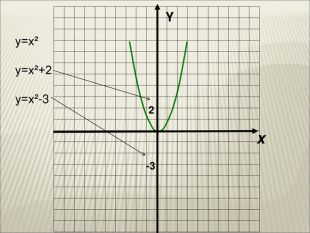
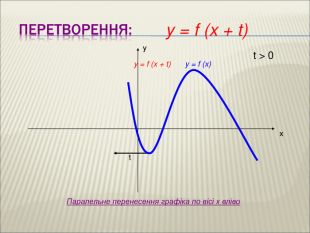
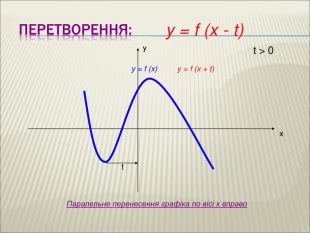
10. Як побудувати графіки функцій y = f (x) + b і y = f (x + a), якщо відомо графік функції y = f (x) Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку