Урок алгебри для 9 класу на тему: "Випадкова подія. Частота і ймовірність випадкової події"

 

 

 

 

 

 

 

 

 

 

Урок алгебри

9 клас

 

 

Випадкова подія.

 

Частота і ймовірність випадкової події

 

 

 

 

 

 

 

 

 

Вчитель Баглюк С. М.

 

        Випадкова подія. Частота і ймовірність випадкової події

Мета:

• Розширити поняття випадкової події та сформувати поняття ймовірності випадкової події

• Формувати вміння знаходити ймовірність випадкової події
• Формувати вміння і навички: визначати вид події (випадкова, вірогідна, неможлива); розв’язувати задачі, що передбачають обчислення ймовірності за формулою
• Ознайомити  з фрагментами історії виникнення теорії імовірностей
• Розширити міжпредметні зв’язки

• Сприяти розвитку логічного мислення, уваги та спостережливості
• Виховання доброти, любові, чесності, вміння співпрацювати

Тип уроку: вивчення нового навчального матеріалу

 

 План вивчення матеріалу

 

1. Актуалізація опорних знань.
2. Поняття випадкової події.
3. Вірогідна, неможлива і довільна випадкова подія.
4. Частота і відносна частота випадкової події.
5.  Означення ймовірності випадкових подій.
6. Приклади розв’язування задач.
7. Підсумки.

 

 

Перевірка домашньої роботи

Мотивація навчання.

• Характерною особливістю курсу шкільної математики, яку ви вивчали до цього часу, є визначеність невідомих. Так, об’єм куба визначається довжиною його ребра, площа круга – його радіусом,  шлях, пройдений тілом – його швидкістю та часом, відсоткова ставка – сумою початкового вкладу тощо.

Але в житті доводиться мати справу з подіями, що залежать від обставин. Наприклад, не можна передбачити, на який білет випаде виграш у майбутньому тиражі лотереї, скільки зерен матиме колос, що виріс із висіяної зернини, хто стане переможцем олімпіади з певного виду спорту тощо.

• Ви знаєте, що перед початком футбольного матчу суддя шляхом жеребкування визначає, яка з команд повинна розпочати гру з центра поля.  Жеребкування проводиться за допомогою монети: один з капітанів команд вибирає “число” чи “герб” , суддя підкидає монету; якщо капітан відгадав, що випаде, то гру розпочинає його команда, якщо ні – команда суперників.

 Чи можна таке жеребкування назвати справедливим?

Взагалі, людська діяльність – це неперервний процес прийняття рішень в обставинах невизначеності чи випадковості:

•  Яку встановити ціну, щоб продати товар і отримати прибуток?
• Яким повинен бути внесок при страхуванні, щоб страхова компанія не мала збитків?

З таким та подібними їм запитаннями люди постійно стикаються в повсякденному житті. Тому варто вміти працювати з випадковими явищами і використовувати їх у житті, наукових дослідженнях тощо.

Наукою,  що займається математичним аналізом випадкових явищ, зокрема, випадкових подій, є “Теорія  ймовірностей”.

       Оголошення теми і мети уроку.

Чи випадковою є ЛЮБОВ ДО МАТЕМАТИКИ?

• Подію, яка в результаті випробування може відбутися або не відбутися, називають…

• Подію, яка в результаті випробування обов’язково відбудеться, називають…

• Подію, яка в результаті випробування не відбудеться ніколи, називають…

• Величину, яка характеризує можливість появи випадкової події, називають …

• Події називаються рівноможливими, якщо …

• Імовірність вірогідної події дорівнює …

• Імовірність неможливої події дорівнює …

 

Запропонуйте  кілька власних прикладів різних видів подій

 

Подію, яка може відбутися, а може й не відбутися в процесі спостереження або експерименту за одних і тих самих умов, називають випадковою подією.
Приклади: випадання «герба», випадання «числа» за підкидання монети; виграш у лотерею ,випадання певної кількості очок за підкидання грального кубика.

 

1.   Частота і відносна частота випадкової події

 

2.   Імовірності вірогідних, неможливих і довільних випадкових подій. Рівноможливі події.

                                                            Подія

 

 

 

 

 

 

 

 

 

 

 

 

 

Формування первинних умінь

Виконання усних вправ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розв’язування задач

 

 

1. Підсумки уроку

Бліц-опитування

1. Наведіть приклади випадкового експерименту та випадкової події.
2. Поясніть на прикладі, що називають частотою та відносною частотою події А.
3. Поясніть зміст статистичного означення ймовірності.
4. Що ви можете сказати про ймовірності неможливих та вірогідних подій?

2. Домашнє завдання

Вивчити  Р. 4 ,§21, виконати №934, №941, №949.

№567. Біатлоніст робить 5 вистрілів по 5 мішенях. За кожного пострілу він може влучити в мішень, а може не влучити.

 Яка з указаних подій є випадковою; неможливою; вірогідною:

•  буде влучено у 4 мішені;
•  не буде влучено в жодну мішень;
•  буде влучено в 6 мішеней?

 

 

 

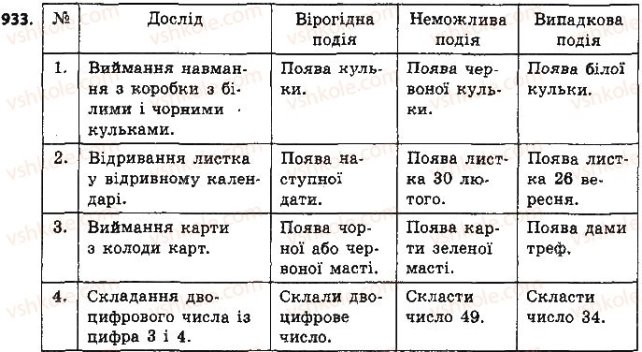
№	Дослід	Вірогідна подія	Неможлива подія	Випадкова подія
1	Виймання навмання кульки з коробки з білими і чорним кульками.
2	Відривання листка у відривному календарі.
3	Виймання карти з колоди карт.
4	Складання двоцифрового числа з цифр 3і4.