Урок "Логарифмічні нерівності"
КОНСПЕКТ УРОКУ
Тема: Логарифмічні нерівності
Мета:
- Навчальна: формування навчок розв’язування найпростіших та більш складних логарифмічних нерівностей;
- Розвиваюча: розвивати вміння розв’язувати логарифмічні нерівності різними способами;
- Виховна: виховувати інтерес до вивчення точних наук; Компетенції:
- Спілкування державною мовою (уміння ставити запитання і розпізнавати проблему; міркувати, робити висновки на основі інформації
Тип уроку: засвоєння нових знань;
Обладнання: опорний конспект, навчальна презентація, мультимедійне обладнання;
Хід уроку
- Організаційний етап
- Привітання
- Перевірка присутніх на уроці
- Перевірка виконання д/з
- Актуалізація опорних знань
1.Дати означення логарифма числа b за основою а ![]()
2. Як поводить себе ф-ція y=![]() , якщо а >1
, якщо а >1
3. Як поводить себе ф-ція y=![]() , якщо 0< а < 1
, якщо 0< а < 1
1.Обчислити
-
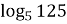 =
=
-
 =
=
-
 =
=
-
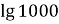 =
=
-
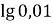 =
=
2. Порівняти х та у
-
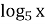 <
< 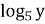
-
 >
> 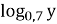
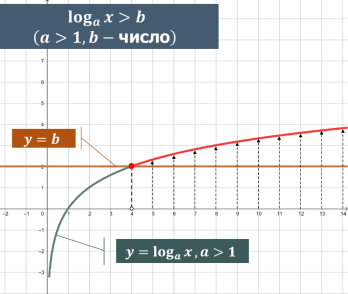
Розглянемо логарифмічну функцію з основою а >1.
Більшому значенню функції відповідає більше значення аргументу, отже
![]()
Знак нерівності не змінюється
Розглянемо логарифмічну функцію з основою 0 < а <1
Більшому значенню функції відповідає менше значення аргументу, отже
![]()
 Знак нерівності змінюється на протилежний
Знак нерівності змінюється на протилежний
- Чи буде виконуватися умова ОДЗ нерівності?
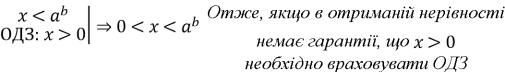
- Закріплення нових знань та вмінь учнів
|
1 )
|
|
|
|
|
Розв’язання:
![]()
Відповідь: ![]()
![]()
Відповідь: ![]()
|
3 )
|
|
|
|
|
Розв’язання:
![]()
![]()
![]()
Відповідь: ![]()
![]()
![]()
![]()
Відповідь: ![]()
№2 Скільки цілих розв’язків має нерівність:
![]()
Розв’язання:
![]()
![]()

Відповідь: нерівність має 21 цілих розв’язків
№ 3. Знайдіть множину розв’язків нерівності:
Розв’язання :
![]()
![]()
![]()
-
ОДЗ:
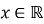
-
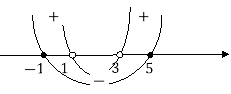 Нулі функції
Нулі функції 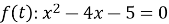
За теоремою Вієта ![]()
*Так як знак нерівності «![]() », оберемо проміжок
», оберемо проміжок ![]()
![]()
![]()
-
ОДЗ:
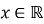
-
Нулі функції
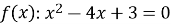
За теоремою Вієта ![]()
*Так як знак нерівності «![]() », оберемо проміжок
», оберемо проміжок ![]()
Відповідь: ![]()


про публікацію авторської розробки
Додати розробку
