Урок алгебри у 8 класі «Обернена пропорційність»

 

 

 

Урок алгебри

у 8 класі

«Обернена пропорційність»

 

 

 

Підготувала

вчитель математики і фізики

загальноосвітньої школи

 І – ІІ ступеня смт Шацьк

Гуж Марія Михайлівна

 

 

 

 

Алгебра, 8 клас

Тема. Обернена пропорційність.

Мета: формувати уявлення учнів про обернену пропорційність як функцію; навчити будувати її графік: дослідити властивості оберненої пропор­ційності, порівняти їх з прямою пропорційністю; розвивати вміння і навички знаходження області визначення та множини значень функції, логічне мислення, уміння знаходити, осмислювати та анал­ізувати інформацію; виховувати інтерес до матема­тики, старанність і працьовитість.

Тип уроку. Урок формування вмінь і навичок.

ХІД УРОКУ

I.  Мотивація навчальної діяльності.

На минулому уроці ми закріплювали вміння і на­вички побудови та дослідження властивостей лінійної функції та окремого її виду — прямої пропорційності.

Як ми можемо спостерігати, у природі більшість процесів та явищ парні. Згадаємо такі природні пари. Наприклад, заряди існують позитивні і ... (негативні), є молодість і ... (старість), життя і ... (смерть), холод і... (тепло), миттєвість і... (вічність), світло і ... (темрява) і т д.

У прямої пропорційності також є свій «анти­под» — це обернена пропорційність.

На цьому уроці ми розглянемо обернену про­порційність як функцію, побудуємо її графік, дос­лідимо її властивості та порівняємо їх з властивос­тями прямої пропорційності.

II.  Актуалізація опорних знань.

Пригадаємо, що ми знаємо про пряму та обер­нену пропорційності на рівні понять.

1.  Що називають прямою пропорційністю? (Залежність між двома величинами, при якій вони одночасно або збільшуються, або зменшуються в од­накову кількість разів.)

2.  Наведіть приклади прямої пропорційності.

3.  Що називають оберненою пропорційністю? (Залежність між двома величинами, при якій із збільшенням однієї величини в кілька разів інша зменшується у стільки само разів, і навпаки.)

4.  Наведіть приклади оберненої пропорційності.

5.  Визначте вид залежності:

1) довжина сторони квадрата і його периметр;

2)  обсяг виконаного домашнього завдання і от­римана оцінка;

3) змарнований час і обсяг виконаної роботи;

4)  оцінки у щоденнику і радість батьків. Розглянемо прояв оберненої пропорційності у явищах природи та галузях людської діяльності. Цим ми ще раз підтвердимо слова Г.Галілея: «Природа формує свої закони мовою математики».

Цей вислів можна вважати епіграфом нашого уроку.

III. Повідомлення учнів.

Учні звітують про самостійно виконану пошу­кову роботу з опису явищ природи та галузей діяль­ності, де зустрічається обернена пропорційність або обернена залежність. (Свої виступи вони супрово­джують показом графіків або ілюстрацій, зображе­них власноруч на аркушах ватману.)

Приклади з біології

У біології можна знайти багато прикладів обер­нено пропорційних і обернених залежностей. На­приклад, чисельність особин певного виду на де­якій території і кількість корму; розміри тварин та їхня рухливість (наприклад, порівняємо ящірку і ва­рана, слона та мишку, горилу та гамадрилу і т.д.); розміри тварин та їх плодючість (маленькі тварини дають більше потомства, ніж великі); діаметр кро­воносних судин і тиск крові (із звужуванням судин тиск крові збільшується).

Приклади з фізики

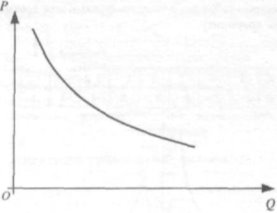
Залежність тиску від площі поверхні Ця залежність задається графіком, зображеним на малюнку.

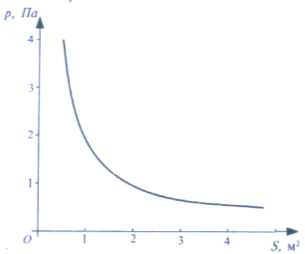
Тиск р, який чинить тіло на деяку поверхню, обернено пропорційний до площі S цієї поверхні:

р = , F = const.

З графіка видно, що із збільшенням площі по­верхні зменшується тиск на неї і навпаки.

Наприклад, людині важко Йти по пухкому снігу — вона буде провалюватися у нього. Але якщо вона надіне лижі, то зможе йти, майже не провалюю­чись. Сила, з якою людина діє на сніг, в обох випадках однакова, проте різна площа поверхні, на яку тисне людина.

Леза ріжучих і вістря колючих інструментів (ножів, ножиць, різців, пилок, голок тощо) добре загострю­ють. Гостре лезо має маленьку площу, тому навіть від малої сили створюється великий тиск, і таким інструментом легко працювати.

Залежність атмосферного тиску

від висоти над рівнем моря

Із збільшенням висоти над рівнем моря змен­шуються тиск і температура повітря.

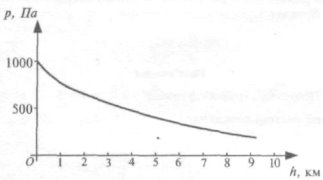
Таке зменшення відбувається поступово. За­лежність атмосферного тиску від висоти над рівнем моря вперше відкрив Блез Паскаль. Група його учнів піднялася на гору То-де-Дом (Франція) і виявила, що на вершині гори стовпчик ртуті на 7,5 см ниж­чий, ніж біля її підніжжя.

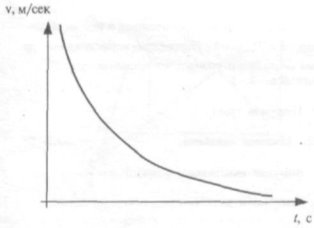
Залежність між швидкістю і часом

Певну відстань з більшою швидкістю можна проїхати за менший час. Якщо зменшувати швидкість, то їхати доведеться довше. Отже, швид­кість і час — обернено пропорційні величини:

v =.

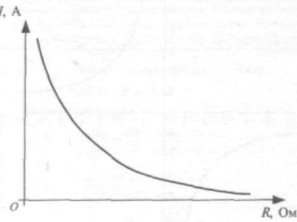
Закон Ома

Сила струму на ділянці кола прямо пропорційна напрузі на кінцях цієї ділянки і обернено пропор­ційна її опору (закон Ома для ділянки кола):

І = , U = const.

Приклади з економіки

В економші прикладом оберненої пропорцій­ності є закон попиту: якщо ціна р якогось товару підвищується і при цьому решта умов залиша­ються незмінними, то попит D на цей товар змен­шується, тобто кількість Q проданого товару змен­шується.

IV. Вивчення нового матеріалу. Формування вмінь і навичок.

1.  Узагальнивши всі наведені учнями формули, можна записати формулу оберненої пропорційності:

y =

де k — сталий коефіцієнт, у — залежна величина (значення функції), х — незалежна змінна (аргу­мент).

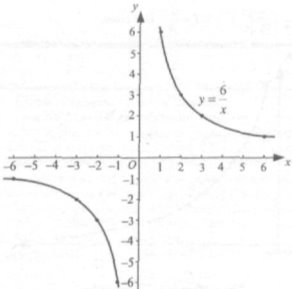
2.  Побудуємо графік функції у = .

Складемо таблицю 1 значень функції для деяких значень аргументу.

Таблиця 1

х	-6	-3	_2	-1	1	2	3	6
у	-1	-2	-3	-6	6	3	2	1

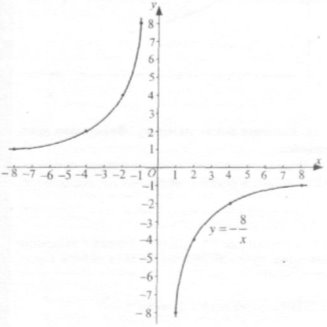
3. Побудуємо графік функції у = - .

Складемо таблицю 2 значень функції для деяких значень аргументу.

Таблиця 2

X	-8	-4	-2	-1	1	2	4	8
y	1	2	4	8	-8	-4	-2	-1

4. Використовуючи побудовані графіки, запов­нимо таблицю 3.

Таблиця 3

Характеристики	Пряма пропорційність	Обернена пропорційність
Формула	у =кх	y =
Область визначення	x R	x 0
Множина значень	y R	y 0
Графік	пряма	гіпербола
k > 0	І і III чверть, зростає	І і НІ чверть, спадає
k < 0	II і IV чверть, спадає	II і IV чверть, зростає
Перетин з осями координат	Перетинає в точці (0; 0)	не перетинає

5. За допомогою графіків функцій можна розв'язу­вати рівняння, які аналітично розв'язати важко.

Приклад 1. Розв'язати рівняння

= 5 - x

Розв'язання

Побудуємо графіки функцій у =  та у = 5 - х в одній системі координат.

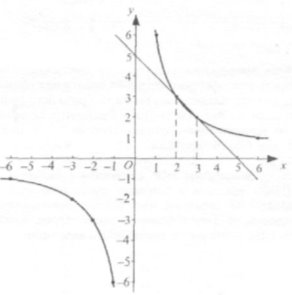
Бачимо,  що  графіки  перетинаються  в  точках,  абсци­си яких х₁ =  2, х₂ = 3. Перевіркою встановлюємо, що названі числа будуть розв'язками рівняння.

Відповідь. 2; 3.

V.  Підсумок уроку.

VI.  Домашнє завдання.

1. Вивчити властивості функції  y = .

2. Розв'язати рівняння:

а) = 4 – x;

б) х+2 = .