Збірка завдань для контрольних і самостійних робіт з математики у 8 класі.
Даний посібник містить добірку завдань для проведення контролю знань, вмінь та навичок учнів з математики у 8 класі. Зміст контрольних робіт відповідає програмі з математики для загальноосвітніх навчальних закладів.
Завдання для контрольних і самостійних робіт подано у двох варіантах і розраховано на один урок, або частину уроку. Вчитель може змінювати обсяг і зміст завдань, враховуючи особливості класу та стан їх підготовки.
Головна мета цієї збірки – допомогти вчителю провести оцінювання знань учнів.
Збірка завдань для контрольних і самостійних робіт
з математики у 8 класі.
Контрольна робота. Повторення за 7 клас. Алгебра. 8 клас.
1 варіант.
1. Розв’язати рівняння: 1) 9х – 7 = 6х + 14; 2) 3( 4 – 2х ) + 6 = - 2х + 4.
2. Побудувати графіки функцій: 1) у = 3 – 2х; 2) у = х – 4.
3. Розв’язати систему рівнянь: ![]()
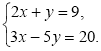
4. Представити у вигляді одночлена: 1) – 4 а3 в5 · 5 а4 в2 ; 2) ( - 3 а7 в2 )4.
5. Розкласти на множники: 1) 9а2 – 16в2; 2) а2 + 10ав + 25в2.
6. За 7кг апельсин та 4кг лимонів заплатили 26грн., а за 5кг апельсин і 2кг лимонів заплатили 16грн. Скільки коштує 1 кг апельсинів і 1кг лимонів?
2 варіант.
1. Розв’язати рівняння: 1) 11х – 9 = 4х + 19; 2) 7х – 5( 2х + 1 ) = 5х + 15.
2. Побудувати графіки функцій: 1) у = 2 – 3х ; 2) у = х – 2.
3. Розв’язати систему рівнянь: 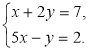
4. Представити у вигляді одночлена: 1) – 3 а2 в4 · 3 а2 в5 ; 2) ( - 4 а2 в6 ) 3.
5. Розкласти на множники: 1) а2 - 4в2 ; 2) а2 – 6 ав + 9в2.
6. За 9 ручок і 4 олівці заплатили 4грн 20коп, а за 2 ручки і 3 олівці заплатили 1грн 25коп. Скільки коштує 1 ручка і 1 олівець?
Контрольна робота. Повторення за 7 клас. Алгебра. 8 клас.
1 варіант.
1. Розв’язати рівняння: 1) 9х – 7 = 6х + 14; 2) 3( 4 – 2х ) + 6 = - 2х + 4.
2. Побудувати графіки функцій: 1) у = 3 – 2х; 2) у = х – 4.
3. Розв’язати систему рівнянь: ![]()
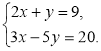
4. За 7кг апельсин та 4кг лимонів заплатили 26грн., а за 5кг апельсин і 2кг лимонів заплатили 16грн. Скільки коштує 1 кг апельсинів і 1кг лимонів?
2 варіант.
1. Розв’язати рівняння: 1) 11х – 9 = 4х + 19; 2) 7х – 5( 2х + 1 ) = 5х + 15.
2. Побудувати графіки функцій: 1) у = 2 – 3х ; 2) у = х – 2.
3. Розв’язати систему рівнянь: 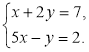
4. За 9 ручок і 4 олівці заплатили 4грн 20коп, а за 2 ручки і 3 олівці заплатили 1грн 25коп. Скільки коштує 1 ручка і 1 олівець?
Контрольна робота. Дії з раціональними дробами. 8 клас.
1 варіант.
1. Знайти область допустимих значень виразу: 1) ![]() ; 2)
; 2) ![]() .
.
2. Скоротити дріб: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
3. Виконати дії: 1) ![]() ; 2)
; 2) ![]() .
.
4. Спростити вираз: 1) ![]() ; 2)
; 2) 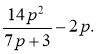
2 варіант.
1. Знайти область допустимих значень виразу: 1) ![]() ; 2)
; 2) ![]() .
.
2. Скоротити дріб: 1) 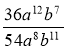 ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
3. Виконати дії: 1) ![]() -
- ![]() ; 2)
; 2) ![]() .
.
4. Спростити вираз: 1) ![]() ; 2) 3у -
; 2) 3у - 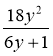 .
.
Контрольна робота. Степінь, стандартний вигляд числа, обернена пропорційність. 8 клас.
1 варіант.
1. Спростити вираз: 1) а7в-2 · а-5в4; 2) 3х-3 · у5 · х6у7.
2. Обчислити: 1) 23 – 1101 ; 2) 52 · 5-3 ; 3) 72 · 74 · 7-6.
3. Записати число у стандартному вигляді: 1) 2530000; 2) 720000; 3) 0,00049;
4) 0,0000015.
4. Обчислити: 1) 4,3 · 107 · ( 1,2 · 106) 2) 1,44 · 106 : ( 1,2 · 103).
5. Побудуйте графік функції ![]() . Визначте, чи належать графіку точки А(4; 2),
. Визначте, чи належать графіку точки А(4; 2),
В(3; 1), С(-1; -8), Д(-6; 2).
2 варіант.
1. Спростити вираз: 1) х6 · у8 · х-4 · у7 ; 2) 2а2в10 · а9в-5;
2. Обчислити: 1) 32 + 1200; 2) 33 · 3-3; 3) 96 · 93 ·9-9.
3. Записати число у стандартному вигляді: 1) 1350000; 2) 640000; 3) 0,00035;
4) 0,00000062.
4. Обчислити: 1) 2,5 · 109 · ( 2,6 · 103) 2) 1,69 · 108 : ( 1,3 · 106).
5. Побудуйте графік функції ![]() . Визначте, чи належать графіку точки А(3; 2),
. Визначте, чи належать графіку точки А(3; 2),
В(2; 4), С(1; 6), Д(-6; 1).
Контрольна робота. Раціональні вирази і рівняння. 8 клас.
1 варіант.
1. Виконати дії: 1) 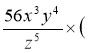 -
- 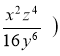 ; 2)
; 2) 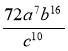 : (24а3в16с8) ;
: (24а3в16с8) ;
3) 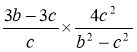 .
.
2. Спростити вираз: ![]() .
.
3. Розв’язати рівняння: 1) ![]() ; 2)
; 2) 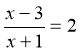 ; 3)
; 3) ![]() .
.
2 варіант.
1. Виконати дії: 1) - 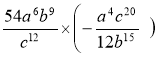 ; 2)
; 2) 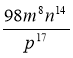 : (49m5n14p2);
: (49m5n14p2);
3) ![]() .
.
2. Спростити вираз: 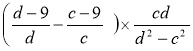 .
.
3. Розв’язати рівняння: 1) ![]() ; 2)
; 2) 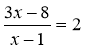 ; 3)
; 3) ![]() .
.
Контрольна робота. Квадратні рівняння. 8 клас.
1 варіант.
1. Розв’язати неповні квадратні рівняння: 1) х2 – 16 = 0; 2) х2 + 5х = 0;
3) 6х2 = 0; 4) х2 + 25 = 0.
2. Розв’язати квадратне рівняння: 1) х2 – 9х + 20 = 0; 2) ![]() ;
;
3) ![]() .
.
3. Розв’язати квадратне рівняння за теоремою Вієта: 1) ![]() ;
;
2) ![]() ; 3)
; 3) ![]() .
.
4. Число 4 є коренем рівняння 3х2 + вх + 4 = 0. Знайти значення в.
5. Знайти сторони прямокутника, якщо одна з них на 3см менша за другу, а
діагональ дорівнює 15см.
2 варіант.
1. Розв’язати неповні квадратні рівняння: 1) 5х2 – 30х = 0; 2) х2 – 25 = 0;
3) 7х2 = 0; 4) х2 + 36 = 0.
2. Розв’язати квадратне рівняння: 1) х2 + 8х – 13 = 0; 2) 25х2 + 60х + 36 = 0;
3) 3х2 – 4х – 5 = 0.
3. Розв’язати квадратне рівняння за теоремою Вієта: 1) х2 - 6х + 8 = 0;
2) х2 - 10х + 21 = 0; 3) х2 + 5х - 24 = 0.
4. Число -3 є розв’язком рівняння 2х2 + 7х + с = 0. Знайти значення с.
5. Діагональ прямокутника на 8см більша за одну із сторін, і на 4см більша за
другу. Знайти сторони прямокутника.
Контрольна робота. Квадратні рівняння. 8 клас.
1 варіант.
1. Розв’язати неповні квадратні рівняння: 1) х2 – 16 = 0; 2) х2 + 5х = 0;
3) 6х2 = 0; 4) х2 + 25 = 0.
2. Розв’язати квадратне рівняння: 1) х2 – 9х + 20 = 0; 2) ![]() ;
;
3) ![]() .
.
3. Розв’язати квадратне рівняння за теоремою Вієта: 1) ![]() ;
;
2) ![]() ; 3)
; 3) ![]() .
.
4. Число 4 є коренем рівняння 3х2 + вх + 4 = 0. Знайти значення в.
5. Знайти сторони прямокутника, якщо одна з них на 3см менша за другу, а
діагональ дорівнює 15см.
2 варіант.
1. Розв’язати неповні квадратні рівняння: 1) 5х2 – 30х = 0; 2) х2 – 25 = 0;
3) 7х2 = 0; 4) х2 + 36 = 0.
2. Розв’язати квадратне рівняння: 1) х2 + 8х – 13 = 0; 2) 25х2 + 60х + 36 = 0;
3) 3х2 – 4х – 5 = 0.
3. Розв’язати квадратне рівняння за теоремою Вієта: 1) х2 - 6х + 8 = 0;
2) х2 - 10х + 21 = 0; 3) х2 + 5х - 24 = 0.
4. Число -3 є розв’язком рівняння 2х2 + 7х + с = 0. Знайти значення с.
5. Діагональ прямокутника на 8см більша за одну із сторін, і на 4см більша за
другу. Знайти сторони прямокутника.
Самостійна робота. Скорочення дробів. 8 клас.
1 варіант.
Скоротити дріб: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() 4 5)
4 5) ![]() ;
;
6)![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
2 варіант.
Скоротити дріб: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() 4 5)
4 5) ![]() ;
;
6)![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
Самостійна робота. Раціональні вирази. ОДЗ. 8 клас.
1 варіант.
1. Вказати допустимі значення виразу: 1) 3х + 4; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
2. При якому значенні змінної , значення дробу дорівнює нулю: 1) ![]() ;
;
2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2 варіант.
1. Вказати допустимі значення виразу: 1) 2х – 3; 2)![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
2. При якому значенні змінної , значення дробу дорівнює нулю: 1) ![]() ;
;
2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
Самостійна робота. Додавання і віднімання дробів. 8 клас.
1 варіант.
1. Виконати дії: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2. Спростити вираз: 1) 4а – ![]() ; 2)
; 2) ![]() .
.
2 варіант.
1. Виконати дії: 1)![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2. Спростити вираз: 1) 3а – ![]() ; 2)
; 2) ![]() .
.
Самостійна робота. Множення дробів. 8 клас.
1 варіант.
Виконати множення: 1) ![]() ; 2)
; 2) ![]() ); 3)
); 3)![]() ; 4) 18у3
; 4) 18у3![]()
![]() ;
;
5) ![]() ; 6)
; 6) ![]() .
.
2 варіант.
Виконати множення: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4) 20х6
; 4) 20х6 ![]() ;
;
5) ![]() ; 6)
; 6) ![]() .
.
Самостійна робота. Множення і ділення раціональних дробів. 8 клас.
1 варіант.
1. Виконати множення: 1) 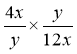 ; 2)
; 2) 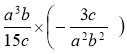 ; 3)
; 3) 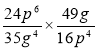 ;
;
4) 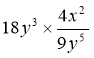 ; 5)
; 5) 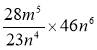 ; 6)
; 6) ![]() .
.
2. Виконати ділення 1) 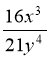 :
: 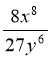 ; 2)
; 2) 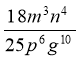 :
: 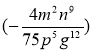 ;
;
3) ![]() :
: 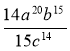 .
.
2 варіант.
1. Виконати множення: 1) 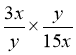 ; 2)
; 2) 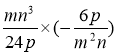 ; 3)
; 3) 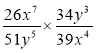 ;
;
4) ![]() ; 5)
; 5) 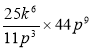 ; 6)
; 6) 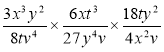 .
.
2. Виконати ділення 1) 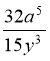 :
: ![]() ; 2)
; 2) 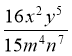 : ( -
: ( - 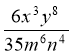 );
);
3) ![]() :
: 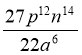 .
.
Самостійна робота. Перетворення раціональних виразів. 8 клас.
1 варіант.
Спростити вираз: 1) 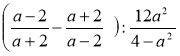 ; 2)
; 2) ![]()
3) ![]() ; 4)
; 4) ![]() .
.
2 варіант.
Спростити вираз: 1) 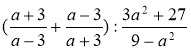 ; 2)
; 2) ![]() ;
;
3) ![]() ; 4)
; 4) ![]() .
.
Самостійна робота. Степінь з цілим показником. 8 клас.
1 варіант.
1. Обчислити: 1) 2-3; 2) 2-4; 3) 2-5; 4) 3-2.
2. Записати у вигляді дробу, який не містить від'ємних показників:
1) 2-5; 2) 4-3; 3) 2а-2; 4) 3х-4.
3. Записати у вигляді степеня з від’ємним показником: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
4. Спростити вираз: 1) 3а-7· 4а5; 2) 4а12 ·7а-14; 3) ( 2-3)4 · 211; 4) ![]() .
.
5. Обчислити: 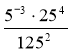 .
.
6. Записати число у стандартному вигляді: 1) 720000; 2) 86000; 3) 0,00013; 4) 0,0000025.
7. Обчислити: 1) (1,2 · 10-4 ) · ( 5 · 10-2 ); 2) ( 4,8 · 103 ) · ( 5 · 102).
2 варіант.
1. Обчислити: 1) 3-3; 2) 5-2; 3) 9-2; 4) 3-2.
2. Записати у вигляді дробу, який не містить від'ємних показників:
1) 5-4; 2) 7-3; 3) 5х-2; 4) 7а-2.
3. Записати у вигляді степеня з від’ємним показником: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
4. Спростити вираз: 1) 4а-12· 6а15; 2) 8а12 ·10а-13; 3) ( 4-2)5 · 49; 4) ![]() .
.
5. Обчислити: 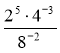 .
.
6. Записати число у стандартному вигляді: 1) 4900; 2) 64000; 3) 0,000029; 4) 0,0023.
7. Обчислити: 1) (1,4 · 10-5 ) · ( 5 · 10-2 ); 2) ( 1,3 · 10-3 ) · ( 5 · 10-5).
Самостійна робота. Квадратний корінь. 8 клас.
1 варіант.
1. Знайти значення корня: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ;
;
6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ; 10)
; 10) ![]() ; 11)
; 11) ![]() ; 12)
; 12) ![]() .
.
2. Спростити вираз: 1) ![]() , якщо
, якщо ![]() ; 2)
; 2) ![]() , якщо
, якщо ![]() < 0;
< 0;
3) ![]() , якщо
, якщо ![]() ; 4)
; 4) ![]() , якщо
, якщо ![]()
2 варіант.
1. Знайти значення корня: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ;
;
6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ; 10)
; 10) ![]() ; 11)
; 11) ![]() ; 12)
; 12) ![]() .
.
2. Спростити вираз: 1) ![]() , якщо
, якщо ![]() ; 2)
; 2) ![]() , якщо
, якщо ![]() < 0;
< 0;
3) ![]() , якщо х < 0 ; 4)
, якщо х < 0 ; 4) ![]() , якщо
, якщо ![]()
Самостійна робота. Квадратний корінь. 8 клас.
1 варіант.
1. Знайти значення: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2. Обчислити вираз: 1) 0,2·![]() -
- ![]() ; 2)
; 2) ![]() +
+ ![]() ; 3) 5·
; 3) 5·![]() .
.
3. Розв’язати рівняння: 1) ![]() = 4; 2)
= 4; 2) ![]() - 8 = 0; 3)
- 8 = 0; 3) ![]() + 3 = 0; 4) х2 = 4; 5) х2 = 0;
+ 3 = 0; 4) х2 = 4; 5) х2 = 0;
6) х2 = - 16.
2 варіант.
1. Знайти значення: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2. Обчислити вираз: 1) 0,1·![]() -
- ![]() ; 2)
; 2) ![]() +
+ ![]() ; 3) 4·
; 3) 4·![]() .
.
3. Розв’язати рівняння: 1) ![]() = 7; 2)
= 7; 2) ![]() - 5 = 0; 3)
- 5 = 0; 3) ![]() + 1 = 0; 4) х2 = 9; 5) х2 = 0;
+ 1 = 0; 4) х2 = 9; 5) х2 = 0;
6) х2 = - 25.
Самостійна робота. Неповні квадратні рівняння. 8 клас.
1 варіант.
Розв’язати рівняння: 1) 5х2 – 20 = 0; 2) х2 + 7х = 0; 3) 3х2 – 18 = 0; 4) 3х2 – 24х = 0;
5) х2 + 25 = 0; 6) (2х – 7 )2 – 7( 7 – 4х ) = 0.
2 варіант.
Розв’язати рівняння: 1) 3х2 – 27 = 0; 2) х2 + 11х = 0; 3) 5х2 – 35 = 0; 4) 5х2 – 30х = 0;
5) х2 + 64 = 0; 6) (3х – 5 )2 – 5( 2 – 6х ) = 0.
Самостійна робота. Квадратні рівняння. 8 клас.
1 варіант.
1. Розв’язати рівняння: 1) х2 + 5х – 14 = 0; 2) х2 – 14х + 40 = 0; 3) 3х2 – 13х + 4= 0;
4) х2 + 6х – 2 =0.
2. При якому значенні а, число 3 є коренем рівняння х2 + ах – 51 =0.
2 варіант.
1. Розв’язати рівняння: 1) х2 - 6х – 27 = 0; 2) х2 – 9х + 20 = 0; 3) 10х2 – 9х + 2= 0;
4) х2 + 8х – 13 =0.
2. При якому значенні а, число 2 є коренем рівняння х2 - ах – 25 =0.
Самостійна робота. Розкладання на множники. 8 клас.
1 варіант.
1. Розкладіть квадратний тричлен на множники: 1) х2 – 5х + 4; 2) 5х2 + 23х – 10;
3) 6х2 – 5х – 6.
2 Виконайте скорочення дробів: 1) 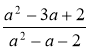 ; 2)
; 2) 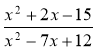 ; 3)
; 3) 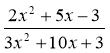 .
.
2 варіант.
1. Розкладіть квадратний тричлен на множники: 1) х2 + 6х + 5; 2) 7х2 - 8х + 1;
3) 10х2 – 17х + 3.
2 Виконайте скорочення дробів: 1) 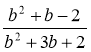 ; 2)
; 2) 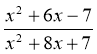 ; 3)
; 3) 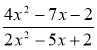 .
.
Контрольна робота. Повторення за 7 клас. Геометрія. 8 клас.
1 варіант.
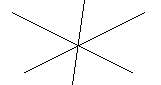 а в с
а в с
2
1
3
1. Дано: а![]() в
в![]() с, <1 = 75°, <2 = 55°. Знайти <3 - ?
с, <1 = 75°, <2 = 55°. Знайти <3 - ?
2. Кути трикутника АВС пропорційні числам 1, 2, і 3. Знайти ці кути.
3. Один із суміжних кутів на 40° менший, від другого кута. Знайти градусні міри цих кутів.
4. Периметр рівнобедреного трикутника дорівнює 17см. Знайти його основу, якщо бічна сторона дорівнює 6см.
2 варіант.
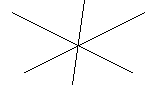 а в с
а в с
2
1
3
1. Дано: : а![]() в
в![]() с, <1 = 25°, <2 = 75°. Знайти <3 - ?
с, <1 = 25°, <2 = 75°. Знайти <3 - ?
2. Кути трикутника АВС пропорційні числам 2, 3, і 4. Знайти ці кути.
3. Один із суміжних кутів на 36° більший, від другого кута. Знайти градусні міри цих кутів.
4. Периметр рівнобедреного трикутника дорівнює 30см. Знайти його бічну сторону, якщо основа дорівнює 12см.
Контрольна робота. Чотирикутники. 8 клас.
1 варіант.
1. В паралелограмі один з кутів у 2 рази більше за другий. Знайдіть кути
паралелограма.
2. Одна із сторін паралелограма на 6см більша за другу сторону. Знайдіть сторони
паралелограма, якщо його периметр дорівнює 48см.
3. У чотирикутнику АВСД проведена діагональ АС. <АСВ = <САД, а
<АСД = <САВ. Довести, що чотирикутник АВСД – паралелограм.
2 варіант.
1. В паралелограмі один з кутів на 60° більший за другий. Знайдіть кути
паралелограма.
2. Одна із сторін паралелограма у 5 разів більша за другу сторону. Знайдіть
сторони паралелограма, якщо його периметр дорівнює 36см.
3. У чотирикутнику АВСД проведено діагональ ВД. <СВД = <АДВ, а
<АВД = <ВДС. Довести, що чотирикутник АВСД – паралелограм.
Контрольна робота. Чотирикутники. 8 клас.
1 варіант.
1. Знайти периметр трикутника, якщо його середні лінії дорівнюють 6см, 9см і
10см.
2. В рівнобічній трапеції АВСД, основи АД і ВС дорівнюють відповідно 17см і
5см. З вершини трапеції точки В проведена висота ВЕ. Знайдіть довжину
відрізка АЕ.
3. Сума двох кутів рівнобічної трапеції дорівнює 100°. Знайдіть кути трапеції.
4. Точки А і В ділять коло на дуги , одна з яких на 80° більша за другу. Знайдіть
міри вписаних кутів які спираються на ці дуги.
2 варіант.
1. Сторони трикутника дорівнюють 10см, 12см і 14см. Знайдіть периметр
трикутника утвореного середніми лініями цього трикутника.
2. У рівнобічній трапеції АВСД висота ВК ділить основу АД на відрізки АК = 4см
і КД = 10см. Знайдіть основу ВС.
3. Кути трапеції дорівнюють 50° і 60°. Знайти інші кути трапеції.
4. Точки С і Д ділять коло на частини одна з яких в 3 рази більша за другу.
Знайдіть міри вписаних кутів, як спираються на хорду СД.
Контрольна робота. Теорема Піфагора. 8 клас.
1 варіант.
1. У прямокутному трикутнику гіпотенуза дорівнює 13см, а один з катетерів
дорівнює 12см. Знайти периметр трикутника.
2. Катети прямокутного трикутника відносяться як 3 : 4, а його гіпотенуза дорівнює
20см. Знайти катети трикутника.
3. У рівнобічній трапеції основи дорівнюють 9см і 21см, висота трапеції дорівнює
8см. Знайти бічну сторону трапеції.
4. З точки А до прямо а проведено дві похилі, проекції яких на пряму а дорівнюють
9см і 16см. Знайти відстань від точки до прямої, якщо одна з похилих на 5см
більша за другу.
2 варіант.
1. У прямокутному трикутнику катети дорівнює 8см і 15см. Знайти периметр
трикутника.
2. Катети прямокутного трикутника відносяться як 12 : 5, а його гіпотенуза дорівнює
39см. Знайти катети трикутника.
3. У рівнобічній трапеції основи дорівнюють 8см і 24см, висота трапеції дорівнює
6см. Знайти бічну сторону трапеції.
4. З точки А до прямо а проведено дві похилі довжиною 15см і 13см. Знайти відстань
від точки до прямої, Якщо різниця проекцій похилих на пряму дорівнює 4см.
Контрольна робота. Розв’язування прямокутних трикутників. 8 клас.
1 варіант.
1. У трикутнику АВС, < с = 90°, ВС = 12см, tg А = 0,8. Знайти сторони АС і АВ.
2. Основа рівнобедреного трикутника дорівнює 10см, а бічна сторона дорівнює
13см. Знайти синус, косинус і тангенс кута при основі трикутника.
3. Обчислити вираз: 1) 2 sin 30° cos 60° + tg 45° cos 60°;
2) 2 cos 45° sin 45° - tg 45°.
4. У прямокутному трикутнику АВС < С = 90°, < В = 60°, ВС = 6см. Знайти інші
елементи трикутника.
2 варіант.
1. У трикутнику АВС, < с = 90°, АВ = 15см, sin А = 0,6. Знайти сторони АС і ВС.
2. Основа рівнобедреного трикутника дорівнює 12см, а висота проведена до основи
дорівнює 8см. Знайти синус, косинус і тангенс кута при основі трикутника.
3. Обчислити вираз: 1) 4 sin 60° cos 30° + tg 60° ctg 30°;
2) cos 45° sin 45° - tg 45° sin 30°.
4. У прямокутному трикутнику АВС < С = 90°, < А = 60°, АС = 8см. Знайти інші
елементи трикутника.
Контрольна робота. Многокутники та їх площі. 8 клас.
1 варіант.
1. У прямокутнику одна із сторін дорівнює 8см, а діагональ – 10см. Знайти площу
прямокутника.
2. Знайти площу прямокутного трикутника, катет якого дорівнює 12см, а гіпотенуза 15см.
3. Знайти площу ромба, якщо його периметр дорівнює 60см, а одна із діагоналей
дорівнює 18см.
4. Знайти площу рівнобічної трапеції з основами 8см і 20см, і периметром 48см.
2 варіант.
1. У прямокутнику одна із сторін дорівнює 12см, а діагональ – 13см. Знайти площу
прямокутника.
2. Знайти площу прямокутного трикутника, катет якого дорівнює 6см, а гіпотенуза 10см.
3. Знайти площу ромба, якщо його периметр дорівнює 80см, а одна із діагоналей
дорівнює 24см.
4. Знайти площу рівнобічної трапеції з основами 12см і 22см, і периметром 60см.
Самостійна робота. Паралелограм. 8 клас.
1 варіант.
1. Сума двох кутів паралелограма дорівнює 76°. Знайдіть кути паралелограма.
2. Одна із сторін паралелограма в два рази більша за сусідню сторону. Знайдіть сторони паралелограма, якщо його Р = 36см.
3.Три попарно паралельні прямі перетинають дві паралельні прямі, скільки паралелограмів при цьому утворилося?
2 варіант.
1. Сума двох кутів паралелограма дорівнює 230°. Знайдіть кути паралелограма.
2. Одна із сторін паралелограма в три рази більша за сусідню сторону. Знайдіть сторони паралелограма, якщо його Р = 48см.
3.Дві паралельні прямі перетинають три попарно паралельні прямі, скільки паралелограмів при цьому утворилося?
Самостійна робота. Паралелограми. 8 клас.
1 варіант.
1. О – точка перетину діагоналей паралелограма АВСД. Знайти периметр трикутника
АОД, Якщо АС = 10см, ВД = 16см, АД = 12см.
2. Одна зі сторін прямокутника на 6см більша, ніж інша. Знайти сторони прямокутника,
якщо Його периметр дорівнює 32см.
3. Сторони ромба дорівнює 7см. Знайти периметр ромба.
2 варіант.
1. О – точка перетину діагоналей паралелограма АВСД. Знайти периметр трикутника
АОВ, Якщо АВ = 5см, АС = 14см, ВД = 12см.
2. Периметр прямокутника дорівнює 72см. Знайти меншу сторону прямокутника, якщо
вона в 2 рази менша від сусідньої сторони.
3. Сторони ромба дорівнює 8см. Знайти периметр ромба.
Самостійна робота. Многокутник. 8 клас.
1 варіант.
1. Знайдіть суму кутів: 1) 7 – кутника; 2) 10 – кутника.
2. Знайдіть внутрішній, центральний і зовнішній кути правильного 9 – кутника.
3. Скільки сторін має многокутник, кожен кут якого дорівнює 1620?
4. Чи існує опуклий многокутник, сума кутів якого дорівнює 8800?
2 варіант.
1. Знайдіть суму кутів: 1) 9 – кутника; 2) 12 – кутника.
2. Знайдіть внутрішній, центральний і зовнішній кути правильного 10 – кутника.
3. Скільки сторін має многокутник, кожен кут якого дорівнює 165,60?
4. Чи існує опуклий многокутник, сума кутів якого дорівнює 17800?
Самостійна робота. Трапеція. 8 клас.
1 варіант.
1. Знайти середню лінію трапеції, якщо її основи дорівнюють 6см і 10см.
2. Висота рівнобічної трапеції, проведена з вершини тупого кута, ділить більшу
основу трапеції на відрізки 3см і 11см. Знайти основи трапеції.
3. Кути трапеції дорівнюють 110° і 60°. Знайти інші кути трапеції.
2 варіант.
1. Знайти середню лінію трапеції, якщо її основи дорівнюють 8см і 12см.
2. Висота рівнобічної трапеції, проведена з вершини тупого кута, ділить більшу
основу трапеції на відрізки 5см і 13см. Знайти основи трапеції.
3. Кути трапеції дорівнюють 70° і 130°. Знайти інші кути трапеції.
Самостійна робота. Подібність трикутників. 8 клас.
1 варіант.
1. Чи подібні трикутники зі сторонами: 5см, 6см, 9см і 20см, 24см, 36см.
2. Δ АВС ∞ ΔА1В1С1 , АВ = 3см, ВС = 4см, В1С1 = 16см, А1С1 = 20см. Знайти інші
сторони трикутників.
3. В ΔАВС ДЕ ║ АС, ВД = 3см, ДЕ = 2см, АВ = 9см. Знайти довжину сторони АС.
2 варіант.
1. Чи подібні трикутники зі сторонами: 8см, 10см, 6см і 4см, 5см, 3см.
2. Δ АВС ∞ Δ А1В1С1 , АВ = 3см, ВС = 5см, В1С1 = 15см, А1С1 = 18см. Знайти інші
сторони трикутників.
3. В ΔАВС ДЕ ║ АВ, ДС = 4см, ДЕ = 5см, АС = 8см. Знайти довжину сторони АВ.
Самостійна робота. Теорема Піфагора. 8клас.
1 варіант.
1. Сторона квадрата дорівнює 5см. Знайти довжину його діагоналі.
2. У прямокутному трикутнику катет дорівнює 9см а гіпотенуза дорівнює 15см.
Знайти другий катет трикутника.
3. У рівнобедреному трикутнику АВС, АВ = ВС = 7см, АС = 6см. Знайти висоту
трикутника ВД, проведену до основи АС.
4. Сторона ромба дорівнює 13см. А одна з його діагоналей дорівнює 10см. Знайти
другу діагональ ромба.
2 варіант.
1. Сторона квадрата дорівнює 7см. Знайти довжину його діагоналі.
2. У прямокутному трикутнику катет дорівнює 6см а гіпотенуза дорівнює 10см.
Знайти другий катет трикутника.
3. У рівнобедреному трикутнику АВС, АВ = ВС = 37см, АС = 24см. Знайти висоту
трикутника ВД, проведену до основи АС.
4. Сторона ромба дорівнює 41см. А одна з його діагоналей дорівнює 18см. Знайти
другу діагональ ромба.
Самостійна робота. Розв’язування прямокутних трикутників. 8 клас.
1 варіант.
1. Розв’язати прямокутний трикутник АВС: 1) <С = 900, <А = 670 , АВ = 10см;
2) <С = 900, АВ = 8см, АС = 5см.
2. В рівнобедреному трикутнику АВС, АВ = ВС, АВ = 6см, <А = 580. Знайти АС.
3. В трапеції АВСД, АД | | ВС, АВ = 8см, ВС = 4см, <А = 300 , <Д = 1200. Знайти АД трапеції.
2 варіант.
1. Розв’язати прямокутний трикутник АВС: 1) <С = 900, <А = 430 , АС = 9см;
2) <С = 900, ВС = 5см, АС = 8см.
2. В рівнобедреному трикутнику АВС, АВ = ВС, АВ = 8см, <А = 670. Знайти АС.
3. В трапеції АВСД, АД | | ВС, АВ = 8см, ВС = 4см, <А = 300 , <Д = 1200. Знайти АД трапеції.
Самостійна робота. Синус, косинус і тангенс кута. 8 клас.
1 варіант.
1. В ΔАВС <С = 90°, ВС = 5см, АВ = 13см. Знайти sin<А, cos<А, tg<А, sin<В, соs<В, tg<В.
2. В ΔАВС <С = 90°, ВС = 2см, cos<В = ![]() . Знайти АВ і АС.
. Знайти АВ і АС.
3. В ΔАВС <С = 90°, АС = 4см, tg <В = 2. Знайти АВ і ВС.
2 варіант.
1. В ΔАВС <С = 90°, ВС = 6см, АС = 8см. Знайти sin<А, cos<А, tg<А, sin<В, соs<В, tg<В.
2. В ΔАВС <С = 90°, АС = 3см, sin<В = ![]() . Знайти АВ і СВ.
. Знайти АВ і СВ.
3. В ΔАВС <С = 90°, ВС = 4см, tg <В = ![]() . Знайти АВ і АС.
. Знайти АВ і АС.
Самостійна робота. Площі фігур. 8 клас.
1 варіант.
1. Один з катетів прямокутного трикутника дорівнює 10см, я його площа – 45см2.
Знайти другий катет.
2. Висота прямокутного трикутника, проведена до гіпотенузи ділить її на частини
довжиною 4см і 9см. Знайти площу цього трикутника.
3. У рівнобічній трапеції основи дорівнюють 4см і 10см, а бічна сторона
дорівнює 5см. Знайти площу трапеції.
2 варіант.
1. Один з катетів прямокутного трикутника дорівнює 8см, я його площа – 32см2.
Знайти другий катет.
2. Висота прямокутного трикутника, проведена до гіпотенузи ділить її на частини
довжиною 4см і 16см. Знайти площу цього трикутника.
3. У рівнобічній трапеції основи дорівнюють 6см і 18см, а бічна сторона
дорівнює 10см. Знайти площу трапеції.


про публікацію авторської розробки
Додати розробку
