Урок алгебри у 9 класі "Квадратична функція, її графік і властивості"

Про матеріал

Розробка узагальнюючого уроку алгебри у 9 класі на тему "Квадратична функція, її графік і властивості".

Мета уроку: узагальнити і систематизувати знання учнів з даної теми, вдосконалити навички побудови графіка квадратичної функції, вміння проводити елементарне дослідження функції; показати застосування квадратичної функції; розвивати обчислювальні навички, графічну культуру,мислення, пам'ять, кмітливість, увагу, ініціативність, самостійність; виховувати навички колективної роботи та співпраці, формувати пізнавальний інтерес.

Перегляд файлу

Конспект уроку алгебри у 9 класі.

Тема. Квадратична функція, її графік та властивості. Узагальнюючий урок.

Мета. Узагальнити і систематизувати знання учнів з даної теми, вдосконалити

навички побудови графіка квадратичної функції, вміння проводити

елементарне дослідження функції; показати застосування квадратичної

функції;

розвивати обчислювальні навички, графічну культуру, мислення, пам'ять,

кмітливість, увагу, ініціативність, самостійність;

виховувати навички колективної роботи та співпраці, формувати

пізнавальний інтерес.

Обладнання: комп’ютери, проектор, презентація, плакат “Застосування

параболи”, роздатковий матеріал, маркери.

Тип уроку: узагальнення і систематизації знань.

Підручник: А. Г. Мерзляк. Алгебра: Підручник для 9 класів загальноосвітніх навчальних закладів. — Х.: Гімназія, 2009. — 320 с.:

Хід уроку.

І. Організаційний момент.

Повідомлення теми, мети уроку.

ІІ. Перевірка домашнього завдання.

№ 371. На рисунках зображено графіки квадратичної функції y = аx² + bх + c. Які знаки мають коефіцієнти a, b, c?

ІІІ. Актуалізація опорних знань і вмінь учнів.

Усне опитування. Паралельно двоє учнів виконують вправу за комп'ютерами за допомогою сервісу LearningApps на повторення графіків елементарних функцій (тип вправи – встановити логічну пару).

Від якого коефіцієнта залежить напрям віток параболи?
Вказати формулу для обчислення абсциси вершини параболи.
Як знайти ординату вершини параболи.
Скільки точок перетину з віссю ОХ має парабола, якщо дискримінант відповідного рівняння від’ємний?
Скільки точок перетину з віссю ОХ має парабола, якщо дискримінант відповідного рівняння додатний?
Скільки точок перетину з віссю ОХ має парабола, якщо дискримінант відповідного рівняння дорівнює 0?
Як знайти точку перетину з віссю ОУ квадратичної функції у = ах² + bх + с?
Чому дорівнює найбільше значення квадратичної функції у = ах² + bх + с, якщо а<0?
Чому дорівнює найменше значення квадратичної функції у = ах² + bх + с, якщо а>0?
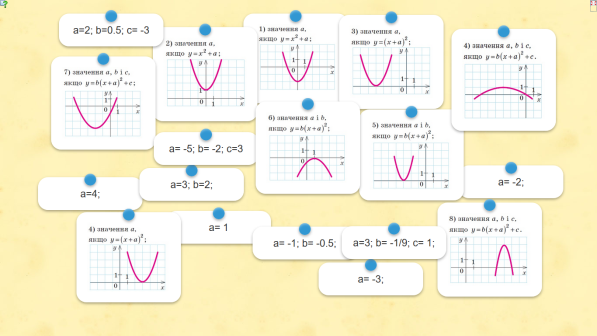
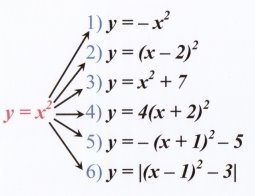$C:\Documents and Settings\Администратор\Мои документы\Мои рисунки\MP Navigator\2008_01_11\IMG_0003.jpg$ Як із графіка функції y = x² за допомогою геометричних перетворень одержати графіки наступних функцій (слайд 1).

Слайд 1

12) Вказати координати вершин кожної з функцій 1) – 6).

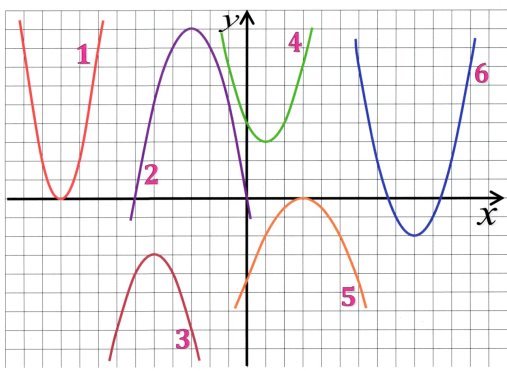$C:\Documents and Settings\Администратор\Мои документы\Мои рисунки\MP Navigator\2008_01_11\IMG_0001.jpg$ 13) Задати формулами функції, графіки яких зображені на малюнку (слайд):

Слайд 2

14) Для яких із цих функцій (слайд 2) виконується умова:

1) a > 0, D > 0;

2) a < 0, D > 0;

3) a > 0, D < 0;

4) a < 0, D = 0;

5) a < 0, D < 0?

ІV. Розв’язування вправ.

Побудувати графік функції y = – x² – 8х – 12 за допомогою елементарних перетворень графіка функції y = x².

Питання до класу: Які перетворення слід виконати, щоб можна було даний графік побудувати за допомогою елементарних перетворень графіка функції y = x²?

y = – x² – 8х – 12 = – ( x² + 8х + 12) = – ( x² + 2 · 4х + 16 – 16 + 12) = – ((x + 4)² – 4) = – (x + 4)²+ 4.

Послідовність побудови:

y = x² y = – x ² y = – (x + 4)² y = – (x + 4)²+ 4

(Поки один із учнів виконує вправу на дошці, групи учнів виконують аналогічну вправу на місцях:

y = x² – 8x + 7 (для середнього рівня)

y = 3x² – 12x + 9 (для достатнього рівня)

y = 0,25x² – 3x + 8 (для високого рівня)

Побудувати графік функції y = 3x² – 12х + 9.

Питання до класу: За яким алгоритмом будується графік квадратичної функції?

Знаходимо нулі функції:

3x² – 12х + 9 = 0;

x² – 4х + 3 = 0;

За теоремою Вієта х₁ = 1; х₂ = 3.

Отже, графік даної функції перетинає вісь х в точках х₁ = 1; х₂ = 3.

Знаходимо координати вершини параболи за формулами: ;

Отже, вершина параболи знаходиться у точці (2; – 3)

Знаходимо точку перетину з віссю y:

y(0) = 9. Отже, (0; 9) – точка перетину з віссю y.

(Поки один із учнів виконує вправу на дошці, групи учнів виконують аналогічну вправу на місцях:

y = 3x² – 6x (для середнього рівня)

y = – 2x² + 8x – 6 (для достатнього рівня)

y = – 0,5x² – 3x + 2,5 (для високого рівня)

Побудувати графік функції y = |3x² – 12х + 9|

Питання до класу: Як із графіка функції y = f(x) одержати графік функції y = |f(x)|? Паралельно будується графік за допомогою програми Geogebra.

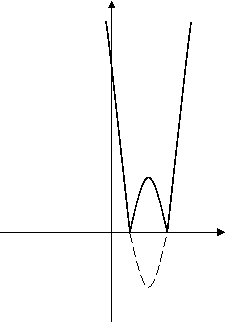
Послідовність побудови: y = 3x² – 12х + 9 y = |3x² – 12х + 9|

y = 3x² – 12х + 9 y = |3x² – 12х + 9|

Побудувати графік функції y = 3x² – 12|х| + 9.

Питання до класу: Як із графіка функції y = f(x) одержати графік функції y = f(|x|)?

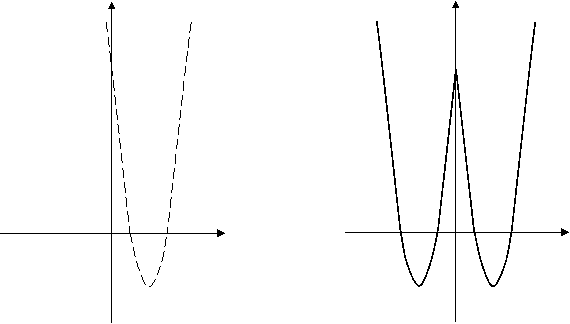
Послідовність побудови: y = 3x² – 12х + 9 y = 3x² – 12|х| + 9

y = 3x² – 12х + 9 y = 3x² – 12|х| + 9

Побудувати графік функції y = |3x² – 12|х| + 9|

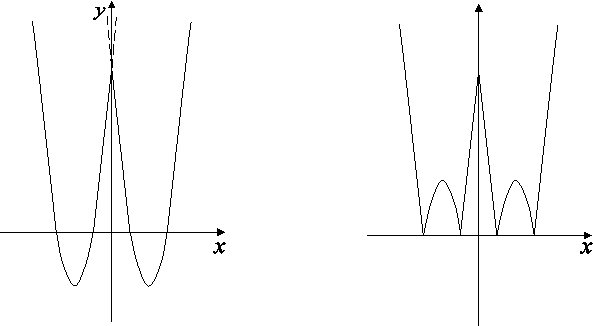
Послідовність побудови: y = 3x² – 12|х| + 9 y = |3x² – 12|х| + 9|

y = 3x² – 12|х| + 9 y = |3x² – 12|х| + 9|

Скільки розв’язків має рівняння |3x² – 12х + 9| = m залежно від параметра m?

Щоб виконати це завдання, потрібно в одній системі координат побудувати графіки функцій y = |3x² – 12х + 9| та y = m для декількох характерних значень m, щоб визначити кількість спільних точок графіків функцій, що й буде вказувати на кількість розв’язків даного рівняння. Виконується за допомогою програми Geogebra.

При m < 0 рівняння розв’язків немає;

при m = 0 рівняння має 2 розв’язки;

при 0 < m < 3 рівняння має 4 розв’язки;

при m = 3 рівняння має 3 розв’язки;

при m > 3 рівняння має 2 розв’язки.

V. Повідомлення учня.

Квадратична функція або її графік, парабола, дуже часто зустрічається в різноманітних галузях науки, виробництва і навіть побуті. Наприклад, у геометрії квадратичною функцією виражається залежність площі квадрата від його сторони, площі круга від його радіуса тощо. У фізиці – це, наприклад, залежність пройденого шляху від часу при прямолінійному рівноприскореному русі.

Широко використовується квадратична функція в економічних розрахунках.

В астрономії парабола також зустрічається. Відомо, наприклад, що якщо космічному кораблю чи штучному супутнику, який обертається навколо Землі, надати другу космічну швидкість, то його траєкторія руху перетвориться з еліптичної в параболічну, і він зможе покинути Землю.

Інженерні розрахунки показують, що різні споруди, мости, арки, мають підвищену міцність.

Ще одне з багатьох застосувань параболи можна побачити на цьому плакаті.

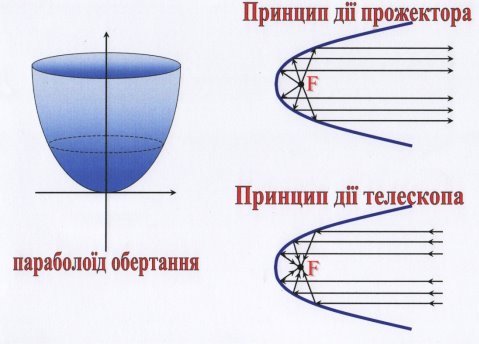
$C:\Documents and Settings\Администратор\Мои документы\Мои рисунки\MP Navigator\2008_01_11\IMG_0001.jpg$

При обертанні параболи навколо осі симетрії одержуємо поверхню, яка називається параболоїдом обертання. Якщо в фокусі такого дзеркального параболоїда помістити джерело світла, то промені світла, відбившись від параболоїда, підуть пучком променів, паралельним до осі симетрії. Цю властивість широко використовують при виготовленні різноманітних прожекторів. Такі самі параболічні дзеркала застосовують в дзеркальних телескопах: світло від далекої зірки йдучи паралельним пучком, відбивається від дзеркала телескопа і збирається в фокусі. За таким самим принципом працюють і супутникові антени, що теж мають форму параболоїда.

VІ. Підсумок уроку.

VIІ. Домашнє завдання.

Підручник, повт. §11.

Вправа 1. Скільки розв’язків має рівняння |3x² – 12|х| + 9| = m залежно від параметра m?