Урок алгебри у 9 класі на тему "Квадратична функція, її властивості та графік"

 Урок алгебри у 9 класі

Тема уроку : Квадратична  функція, її  властивості  та  графік

Мета уроку: формувати компетентність учнів розпізнавати квадратичну функцію серед інших елементарних функцій, наводити її приклади, знаходити координати вершини та напрям віток графіка квадратичної функції, виконувати побудову графіка за вивченим алгоритмом та вказувати   властивості квадратної функції за отриманим графіком; розвивати компетентність вільно висловлюватися з теми, сприяти вихованню пізнавального інтересу через розуміти практичне застосування вивченого поняття.

        Завдання уроку  - навчити учнів:

- розпізнавати квадратичну функцію серед інших елементарних функцій, наводити приклади;

- знаходити координати вершини та напрям віток графіка квадратичної функції;

- виконувати побудову графіка за вивченим алгоритмом;

- за графіком квадратичної функції вказувати  властивості функції.

Тип  уроку: формування знань, вироблення первинних умінь та навичок

Обладнання: дошка, «чарівна скринька», зошити, проектор, презентація, дидактичний  матеріал, роздавальний  матеріал(картки), листки оцінювання.

                                                  Хід  уроку

І. Організаційний етап.

  (Слайд 1)  Доброго дня! Я рада вас бачити сьогодні на уроці. З яким настроєм ви прийшли на цей урок ? Оберіть відповідний смайлик. У мене в руках чарівна скринька. Я пропоную вам написати на обраному смайлику ваші очікування від уроку, ми їх заховаємо до цієї скриньки, щоб вони справдилися (діти озвучують свої очікування).   А я у свою чергу кожному з вас хочу побажати, щоб на цьому уроці ви були (Слайд 2) 

«У»- успішними

«С» - спостережливими

«П» - прогресивними

«І» - ініціативними

«Х» - хоробрими.

           Але успіх – це тільки  10 % таланту і  90% щоденної наполегливої праці.   Отже, починаємо працювати!

 ІІ.  Мотивація діяльності учнів 

      Слово  вчителя. Подивіться, будь ласка, на екран (слайд 3). Що ви бачите на слайдах? Давайте поглянемо на це  з точки зору алгебри. Що об’єднує усі зображення?

А чи знаєте ви, що практика та інженерні розрахунки показують, що різні споруди, мости, арки у формі параболи мають підвищену міцність.

ІІІ. Актуалізація опорних знань 

Тож ми з вами переконалися, що парабола та її властивості широко використовуються людством. А як називається функція, графіком якої є парабола? А оскільки, як ми вже сказали, квадратна функція є окремим випадком квадратичної,  згадаємо її властивості.

Вправа «Незакінчене речення» (у вигляді ромашки)

1.                   Функція - …
2.                   Графіком функції - …
3.                   Квадратна функція – це …
4.                   Побудуйте графік у=х²
5.                   Напрям віток параболи залежить ..
6.                   Нулі функції - …
7.                   На  графіку нулі функції – це …
8.                   Функція називається зростаючою на  проміжку , …
9.                   У спадної функції ..
10.               Проміжки знакосталості - …
11.               Охарактеризуйте графік функції y = x².

ІV. Оголошення теми та мети уроку

Так, квадратна, яка є окремим випадком квадратичної. З якою ми ще не знайомилися. Тому я пропоную вам самостійно визначити тему та завдання нашого уроку (слайд 4).

V.  Вивчення нового матеріалу (первинне засвоєння)

Отже,  на   ми з вами з’ясуємо ( план  на дошці):

1. Означення квадратичної функції.
2. Побудова графіка квадратичної функції.
3. Властивості квадратичної функції

                 Я пропоную нам з вами створити візитівку квадратичної функції. Тому під час роботи ми будемо фіксувати результати нашої у роботи   у цій таблиці.

 

Квадратична функція

Означення		у=aх2+bх+с, де а≠0
Де зустрічаємо у житті		Арки, веселка, фонтани, мости, траєкторія руху  м’яча
		а>0		а<0
Графік		Парабола з вершиною  (хв; ув)
Напрям  гілок		Вгору	Вниз
Область визначення		(-∞;+∞)	(-∞;+∞)
Область значень		[ув;  +∞)	(-∞; ув]
Координати вершини параболи		хв = -      ув =f(хв)
Вісь симетрії		Пряма, що проходить через вершину параболи паралельно осі 0у (х=хв)
Нулі функції		Корені рівняння aх2+bх+с =0 або точки перетину параболи з віссю Ох
Проміжок зростання		[хв;  +∞)		(-∞; хв]
Проміжок спадання		(-∞; хв]		[хв;  +∞)
Найбільше значення функції		Не існує		ув
Найменше значення функції		ув		Не існує
Проміжки знакосталості	у>0
	у<0

 

5.1. Робота з підручником

           Відкрийте підручники на стор. 98 і з’ясуйте, що називають квадратичною функцією. Давайте перевіримо себе ( слайд 5)

           Що запишемо до таблиці? Формулу у=aх²+bх+с, де а≠0 Чому коефіцієнт а не має дорівнювати нулю?

       Як  називається  графік  квадратичної  функції?  (слайд 6). Парабола, гілки якої  направлені   вгору (якщо а>0)  або   вниз (якщо  а<0). Що занесемо до таблиці?

5.2. Вправа «Знайди зайве».

Давайте спробуємо знайти квадратичну функцію серед інших елементарних 

/Учні обирають із запропонованих квадратичну пояснюють та прикріпляють на дошку. Потім наводять свої приклади./

5.3. Робота з алгоритмом

А тепер спробуємо побудувати графік квадратичної функції. У вас є картка з алгоритмом побудови. Ознайомтеся з нею.

 Загальний спосіб побудови графіка квадратичної функції  у = ах2+bх+с :

1. Будуємо вершину параболи, обчисливши її  координати за формулами: х_в = - 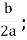     у_в =f(х_в)
2. Проводимо через побудовану вершину вісь симетрії — пряму, паралельну осі 0у, х=х_в.
3. Будуємо кілька точок, що належать графіку даної функції.
4. Будуємо точки, симетричні їм відносно вісі симетрії параболи.
5. Сполучаємо побудовані точки  плавною лінією

Що нового для вас є у цьому алгоритмі? Так, координати вершини (слайд 7).

 

VІ.  Осмислення нових знань та умінь

 

1.        Побудова графіка (слайд 8)

Виконаємо це на практиці. Побудуємо графік функції у = х² + 2х – 3.

 Що занесемо до таблиці - візитівки? Так,  координати вершини  та вісь симетрії.

 6.2. Фізкультхвилинка

Учневі пропонуються перекинути м’яч  або забити гол.

А чи знаєте, що рівняння руху м’яча  також описує квадратична функція.  І як далеко та як високо полетить м’яч,  теж допомагає визначити квадратична функція. (слайд 9)

Тому я пропоную продовжити роботу і перейти до третього пункту нашого плану.

2.        Робота з графіком

Спробуємо визначити властивості функції (слайд 10)

1. Область визначення
2. Область значень
3. Нулі функції
4. Проміжок зростання
5. Проміжок спадання
6. Проміжки знакосталості у>0, у<0
7. Найбільше значення функції у_max=  , при х = .

 

VІІ.  Закріплення , узагальнення матеріалу 

7.1. Робота з підручником ( №434)

Побудувати графік функції та вказати її властивості (слайд 11-12)

 

VІІІ.  Контрольно –корегуючий етап 

 

8.1.   Виконання тесту (слайд 13-16)

8.2. Колективне заповнення  візитівки квадратичної функції (таблиці). Самостійна робота

 

 

ІХ.  Підведення підсумків. Рефлексія

Складання історії ( елементи  методу сторітеллінгу) (слайд 17)

А зараз пропоную повернутися до нашої чарівної скриньки. Чи всі ваші очікування справдилися? Але у скриньці ще є ось такий капелюх . Як у справжнього артиста. Тому я пропоную вам теж  на хвилинку перетворитися на артиста розмовного жанру і допомогти мені розповісти маленьку історію.

   Оскільки у березні у нашій країні нас чекають вибори, то і в країні Математики теж таке можливо.   Представляти свою родину в уряді країни довіряють найкращим.  Спробувати виграти вибори і потрапити   в уряд  від сім'ї функцій вирішила і квадратична функція.  Обов’язковою умовою конкурсу є розповідь про себе. Квадратична функція розпочала  свою розповідь про себе  так….

 

Х.  Домашнє завдання

Вивчити правила параграфа 11, виконати №435 , 437, 440 (додатково), знайти приклади з життя, пов’язані з квадратичною функцією (слайд 18)

 

 

 

ДОДАТКИ

                                              Лист  оцінювання                                   П.І.  учня    ___________________________________________

 

Вид роботи	Кількість  балів	Загальна кількість балів
Усне опитування	По  1 балу
Гра «Знайди зайве»	По  1 балу
Робота біля дошки	6 балів
Самостійна робота	6  балів
Тест	8  балів
УСЬОГО   БАЛІВ
ОЦІНКА

 

«10-12» - 23  і  більше  балів,

«7-9» - від  17 до 22 балів,

«4-6» - від  11 до 16 балів,

«1-3» - 10 балів і менше

 

 

 

 

 

Візитівка «Квадратична функція»

 

 

Означення		у=aх2+bх+с, де а≠0
Де зустрічаємо у житті		Арки, веселка, фонтани, мости, траєкторія руху  м’яча
		а>0		а<0
Графік		Парабола з вершиною  (хв; ув)
Напрям  гілок		Вгору	Вниз
Область визначення		(-∞;+∞)	(-∞;+∞)
Область значень		[ув;  +∞)	(-∞; ув]
Координати вершини параболи		хв = -      ув =f(хв)
Вісь симетрії		Пряма, що проходить через вершину параболи паралельно осі 0у (х=хв)
Нулі функції		Корені рівняння aх2+bх+с =0 або точки перетину параболи з віссю Ох
Проміжок зростання		[хв;  +∞)		(-∞; хв]
Проміжок спадання		(-∞; хв]		[хв;  +∞)
Найбільше значення функції		Не існує		ув
Найменше значення функції		ув		Не існує
Проміжки знакосталості	у>0
	у<0

Загальний спосіб побудови

графіка квадратичної функції  у = ах2+bх+с :

 

1. Будуємо вершину параболи, обчисливши її  координати за формулами: х_в = - 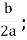     у_в =f(х_в)
2. Проводимо через побудовану вершину вісь симетрії — пряму, паралельну осі 0у, х=х_в.
3. Будуємо кілька точок, що належать графіку даної функції.
4. Будуємо точки, симетричні їм відносно вісі симетрії параболи.
5. Сполучаємо побудовані точки  плавною лінією.

Тест №1

D>0;a<0
D<0;a>0
D<0;a<0
D=0;a>0

 

Самостійна робота

1. Обери квадратичні функції (обведи у кружечок)

1. у=2х² + 3х;           2) у = -х² + 3х - 2;           2) у = -х³ + 3х² – 2.         

 

2. Визнач напрям гілок параболи (познач поряд):

1) у = -х² + х - 2;       2)    у = -х^2- - 3х - 2;       3) у = 6х² – 2.              

3. Визнач координати вершини графіка функції  у = х² - 8х + 7.          
4. Побуду графік функції у = -х²+6х-5.
5. Вкажи властивості  функції за побудованим графіком.