Урок алгебри в 9 класі "Розв'язування текстових задач складанням систем рівнянь другого степеня з двома змінними.
Алгебра 9 клас УРОК № 37
Тема уроку. Розв'язування текстових задач складанням систем рівнянь з двома змінними.
Мета уроку:
навчальна: удосконалити вміння розв'язувати системи рівнянь ; формувати вміння розв'язувати прикладні задачі складанням систем рівнянь;
розвивальна: розвивати пізнавальну компетентність учнів, логічне мислення; формувати вміння вибирати і використовувати необхідну інформацію для розв'язування прикладних задач, застосовувати знання в нових ситуаціях;
виховна: виховувати інтерес до вивчення математики, творче ставлення до справи, цілеспрямованість, працьовитість, наполегливість, відповідальність, уміння працювати в групі.
Тип уроку: удосконалення та застосування знань і вмінь.
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Актуалізація опорних знань
![]()
- Що записано на дошці?
- Що значить розв’язати СР?
- Що є розв’язком СР?
- Які знаєте методи розв’язування СР? (графічний, підстановки, додавання)
- В чому вони полягають та яка доцільність їх використання?
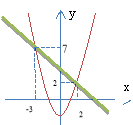 Добрати раціональний метод та розв’язати СР.(учні виконують самостійно способом підстановки, додавання, на дошці - графічно)
Добрати раціональний метод та розв’язати СР.(учні виконують самостійно способом підстановки, додавання, на дошці - графічно)
![]() графік парабола
графік парабола ![]()
|
Х |
0 |
4 |
|
У |
4 |
0 |
![]() графік пряма
графік пряма ![]()
Відповідь: (2;2) ; (-3;7)
Перевірка домашнього завдання
Учитель збирає зошити з виконаною домашньою самостійною роботою. Для учнів, що мали труднощі з виконанням завдань цієї роботи, треба завчасно приготувати правильні розв'язання, які роздати для самостійного опрацювання вдома.
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Яка необхідність вміти розв’язувати СР?
(вміти застосовувати знання та вміння в життєвих ситуаціях)
(формулюється мета уроку: вивчити схему розв'язування задач складанням систем рівнянь з двома змінними та виробити вміння застосовувати цю схему при розв'язуванні практичних задач.)
- Вже розв’язували задачі на складання рівнянь
Складіть рівняння за даною умовою:
- перше число х, друге - у, перше число на 3 більше за друге;
- одне число х, друге у, добуток 15;
- довжина прямокутника а, ширина b, площа 48 см2
- гіпотенуза прямокутного трикутника 13, катети х, у;
- швидкість велосипедиста х км/год, швидкість пішохода у км/год, за 2 год пішохід проходить на 1 км менше, ніж велосипедист проїжджає за 1 год.
ІV. Формування знань
План вивчення нового матеріалу
- Загальна схема розв'язування задач складанням системи рівнянь з двома змінними.
- Приклади розв'язування задач за складеною схемою.
Опорний конспект
|
Як розв'язати задачу, склавши систему рівнянь з двома змінними |
|
1. Виділяємо в умові задачі дві невідомі величини (шукані або ті, через які можна виразити шукані величини) і позначаємо їх буквами х і у. |
|
2. За умовою задачі складаємо два рівняння зі змінними х і y. |
|
3. Розв'язуємо систему цих рівнянь. |
|
4. Розтлумачуємо знайдені розв'язки відповідно до умови задачі. Записуємо відповідь. |
V. Формування вмінь
Задача 1
Навколо земельної ділянки 24 а(2400м2) необхідно поставити огорожу. Закупили 220м паркану. Які були розміри земельної ділянки, якщо паркану вистачило без залишку ?
 Розв’язування
Розв’язування
Нехай
а(м) – довжина земельної ділянки;
в (м) – ширина земельної ділянки.
Так як площа земельної ділянки S=2400 м2, то а*в =2400
Так як довжина паркану (периметр земельної ділянки) Р=220 м, то (а + в)*2=220
Отже, маємо систему рівнянь:![]()
Відповідь: 30м і 80м
Задача2 (аналогічна №14.12)
Площа грального поля стадіону прямокутної форми дорівнює 180 м2. Якщо довжину поля зменшити на 3 м, а ширину зменшити на 2 м, то отримаємо поле площею 120 м2. Знайдіть довжини сторін грального поля стадіону.
 Розв’язування
Розв’язування
Нехай
а(м) – початкова довжина грального поля стадіону;
в (м) – початкова ширина грального поля стадіону.
Так як площа грального поля S=180 м2, то а*в =180
Так як розміри поля змінили, то
а-3 (м) – нова довжина грального поля стадіону;
в-2 (м) – нова ширина грального поля стадіону.
Так як площа нового грального поля S= 750м2, то (а-3)*(в-2) =120
Отже, маємо систему рівнянь:![]()
Відповідь: 15 м і 12 м. або 18м і 10 м
Учні демонструють індивідуальні проекти
Задача 3*. (№14.14.)
Із металевого листа прямокутної форми виготовили відкриту коробку. Для цього в кутах листа вирізали квадрати зі стороною 4 см. Знайдіть довжину та ширину листа, якщо його периметр дорівнює 60 см, а об’єм коробки — 160 см3.
 Розв’язування
Розв’язування
Нехай
а(м) – довжина металевого листа;
в (м) –ширина металевого листа.
а-8= а1 (м) – довжина основи коробки;
в-8= в1 (м) – ширина основи коробки.
Так як периметр металевого листа Р=60 см, то (а+в)*2 =60
Так як об’єм коробки V=a1*b1*h =160 см3 , то (а-8)*(в-8)*4=160
Отже, маємо систему рівнянь:![]()
Відповідь: 18 см і 12 см.
 Задача 4* (№14.18.)
Задача 4* (№14.18.)
По круговій доріжці завдовжки 800 м в одному напрямі рухаються двоє ковзанярів. Один ковзаняр пробігає коло на 24 с швидше за другого й наздоганяє його через кожні 8 хв. Знайдіть швидкість кожного ковзаняра.
Розв’язування
Нехай
х(м/хв) – швидкість І ;
у (м/хв) – швидкість ІІ.
![]() (хв.) - час руху І для подолання кола,
(хв.) - час руху І для подолання кола,
![]() (хв.) - час руху ІІ для подолання кола,
(хв.) - час руху ІІ для подолання кола,
Так як один ковзаняр пробігає коло на 24 с =![]() швидше за другого, то
швидше за другого, то
t2 – t1 = 24c або ![]() =
=![]()
Так як один ковзаняр наздоганяє другого через кожні 8 хв., то SI –SII =800
Так як
SI =8х (м) – пробігає І за 8хв до зустрічі;
SIІ =8у (м) – пробігає ІІ за 8хв до зустрічі , то маємо рівняння 8х-8у =800
Отже, маємо систему рівнянь: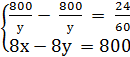
Відповідь: 500 м/хв. і 400 м/хв.
Задача 5*. (№14.21)
Якщо відкрити одночасно дві труби, то басейн буде наповнено водою за 12 год. Якщо спочатку наповнювати басейн тільки через першу трубу протягом 5 год, а потім тільки через другу протягом 9 год, то водою буде наповнено половину басейну. За скільки годин можна наповнити басейн через кожну трубу?
Розв’язування
Нехай
х(год) – час роботи І труби, щоб наповнити басейн;
у(год) – час роботи ІІ труби, щоб наповнити басейн;
![]() - часина басейну, що заповнює І труба за одну годину,
- часина басейну, що заповнює І труба за одну годину,
![]() - часина басейну, що заповнює ІІ труба за одну годину,
- часина басейну, що заповнює ІІ труба за одну годину,
Так як дві труби заповнює басейн за 12 годин, то ![]() =
=![]()
Так як за 5 год роботи І труби і 9 год роботи ІІ заповниться лише половину басейну, то
![]() =
=![]()
Отже, маємо систему рівнянь: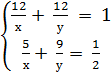
Відповідь: 16 год. і 48 год.
VI. Підсумки уроку
Контрольні завдання
- Укажіть систему, яка відповідає умові задачі: «Число х на 3 менше від числа у, а їхній добуток дорівнює 88. Чому дорівнюють ці числа?».
1) 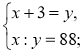 2)
2) 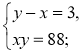 3)
3) 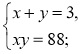 4)
4) 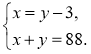
- Укажіть рівняння, яке відповідає умові задачі: «Периметр прямокутника дорівнює 28 дм, а діагональ дорівнює 10 дм. Знайдіть сторони а і b прямокутника».
1) 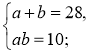 2)
2) 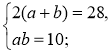 3)
3) 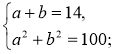 4)
4) 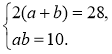
VIII. Домашнє завдання
Кожний з двох принтерів має надрукувати текстовий файл обсягом 120 сторінок. Перший принтер за 1 хвилину друкує на 2 сторінки менше, ніж другий, і тому пропрацював на 3 хвилини довше. Скільки сторінок за хвилину друкує кожен принтер?

про публікацію авторської розробки
Додати розробку
