Урок.Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії. Сума n перших членів арифметичної прогресії

Урок-лекція

алгебра, 9 клас

Тема уроку. Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії. Сума  n перших членів арифметичної прогресії.

Мета: формувати означення арифметичної прогресії, формувати поняття n-го члена арифметичної прогресії, поняття суми  n перших членів арифметичної прогресії, розвивати вміння аналізувати, систематизувати, застосовувати теоретичні відомості для розв’язування вправ; виховувати інтерес до знань, до роботи з комп’ютерною технікою.

Обладнання:  комп’ютер, мультимедійна дошка.

Епіграф:                                  Те, що я чую, я забуваю.

Те, що я бачу й чую, я трохи пом’ятаю.

Те, що я бачу, чую й обговорюю, я починаю розуміти.

Коли я чую, бачу, обговорюю й роблю,

я набуваю знань і навичок.

Конфуцій

                                    Хід уроку

І. Організаційна частина. Актуалізація опорних знань.

• На минулому уроці ми з вами дали означення послідовності. Пропоную створити «Асоціативний кущ» на цей термін.

СЛАЙД 1

ІІ. Перевірка домашнього завдання. (усно)

ІІІ. Вивчення нового матеріалу.

• Послідовність, прояку ми сьогодні будемо говорити на уроці, є особливою. Її назва – арифметична прогресія.

Тема, яку ми сьогодні вивчатимемо, називається «Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії. Сума  n перших членів арифметичної прогресії.»

СЛАЙД 2

СЛАЙД 3

СЛАЙД 4

СЛАЙД 5

• Можемо помітити, що в цих послідовностях кожний член, починаючи з другого, можна знайти додаванням до попереднього одного й того самого числа. Такі послідовності називають арифметичними прогресіями. Сформулюйте, будь-ласка, означення  арифметичної прогресії.

Арифметичною про­гресією називається послідовність, кож­ний член якої, починаючи з другого, дорів­нює попередньому, складеному з одним і тим самим числом.

СЛАЙД 6

Запишемо це означення рекурент­ною формулою

Число d називають різницею ариф­метичної прогресії 

СЛАЙД 7

СЛАЙД 8

• Які з цих послідовностей є зростаючими (спадними)?
• Від чого це залежить?
• Спробуйте в кожному з розв’язаних прикладів знайти 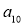; 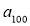. Для цього вам доведеться обчислити всі попередні елементи. Тому, крім рекурентної формули, що задає прогресії. Потрібно знайти ще й формулу n-го члена, яка дає змогу за номером елемента обчислити його.

 (Вивод формули учителем)

a₂ =a_{1 +} d;

a₃ =a_{2 +} d= a_{1 +} 2d;

a₄ =a_{3 +} d= a_{1 +} 3d;

a₅ =a_{4 +} d= a_{1 +} 4d;

a_n =a_{1 +} (n-1)d

СЛАЙД 9

СЛАЙД 10

• Усна вправа. Виразіть, користуючись формулою , , ,, , .

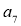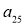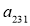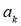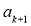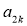СЛАЙД 11

 Історична довідка (готують учні).

У перекладі з латинської слово про­гресія означає рух уперед.

Прогресії відомі здавна, а тому не можна сказати, хто їх відкрив. Адже і натуральний ряд 1, 2, 3,4,... — це ариф­метична професія, в якої а₁ =1; d=1. .

Під час розкопок у Єгипті було знайде­но папірус, що датується 2000 р. до н.е., але і його було переписано з іншого, ще давнішого, віднесеного до третього тисячоліття до н.е. Учені розшифрува­ли текст папірусу і прочитали кілька задач. Зміст деяких з них дає мож­ливість віднести їх до задач на прогресії.

Задачі на прогресії зустрічаються в одній з найдавніших пам'яток пра­ва — «Руській правді», укладеній ще за Київського князя Ярослава Мудро­го (XI ст.). Там є стаття, присвячена обчисленню приплоду від 22 овець за 12 років за умови, що кожна вівця що­річно приносить 1 вівцю і 2 барани.

Значна кількість задач на професії є в «Арифметиці» Л.Магницького (1703), що була основним математич­ним підручником у Росії протягом майже півстоліття.

Учнівська презентація

• А тепер подумаємо, чому професію назвали арифметичною.

Розгляньте будь-який член ариф­метичної прогресії. Як він пов'язаний з його наступним і попереднім чле­нами? Виявляється, що він дорівнює середньому арифметичному наступно­го і попереднього членів, тобто

 Звідси і назва прогресії – арифметична

Цю властивість можна узагальнити і сформулювати так: сума двох членів скінченої арифметичної прогресії, рівновіддалених від її кінців, дорівнює сумі крайніх членів.

СЛАЙД 12

Використовуючи означення арифметичної прогресії, одержимо її члени:

a₁, а₁+d, а₁+2d, а₁+3d, а₁+4d, а₁+5d, а₁+6d, а₁+7d, …

Звідси а_n=а₁+(n-1)d  Це формула n-го члена арифметичної прогресії.

- Звідси і назва прогресії. Це і є характеристична властивість арифметичної прогресії.

Задача. Учитель запропонував знайти суму всіх натуральних чисел від 1 до 40; думав, що школярі довго додаватимуть сорок чисел. А малий Карл Гаус (згодом відомий німецький математик) завдання виконав за хвилину. Як він міркував? Спробуйте завдання виконати усно.

Послідовність чисел від 1 до 40 становить арифметичну прогресію, у якої a₁ = 1, d=1, n=40, n – кількість перших членів арифметичної прогресії. Малий Гаус помітив, що сума двох членів скінченої арифметичної прогресії, рівновіддалених від її кінців, дорівнює сумі крайніх членів. Справді, якщо , то

і т. д.

Виведемо тепер формулу суми перших n членів арифметичної прогресії. Нехай S_n – сума перших n членів арифметичної прогресії a₁, a₂, a₃ …a_n …

На наступному слайді учням демонструється доведення:

Користуючись цією формулою знайти суму перших двадцяти членів арифметичної прогресії 5, 7, 9, ….

a₁ = 5

n = 20

S₂₀ - ?

Розв’язання

d = 7 – 5 = 2

a₂₀ =  а₁ + 19 d = 5 + 19 · 2 = 43

Відповідь. 480.

- Давайте подумаємо, чи існує відповідність між номером члена прогресії та значенням члена цієї прогресії?

- Якою формулою задається така залежність?

- Як в математиці називається така відповідність?

- Яка функція задає арифметичну прогресію?

a_n =  a₁ + d (n – 1)

a_n = y,  n =  x,   x є N

y =  a₁ +  d( x – 1) =  a₁ +  dx –  d =  dx + ( a₁ –  d) =  kx +  b

- Отже, лінійна функція, визначена на множині натуральних чисел, визначає арифметичну прогресію. Побудуємо графік.

На дисплеї комп’ютера

a_n

                                                           ( a_n ): 1;3; 5; 7;9;………….

                                                             n

              1   2   3   4    5                   

- Легко помітити, що всі побудовані точки належать прямій.

  IV. Підсумок уроку.  

V. Домашнє завдання.  Прочитати п.10.2(ст. 214-216),п.10.3(ст. 220-222), вивчити конспект, виконати вправу