Матеріал для факультативу: "Задачі з параметрами"
Задачі з параметрами
Зміст
Вступ _______________________________________________________ 3
Розв’язування рівнянь, нерівностей та систем з параметрами_____ 4
Розділ І. Розв’язування рівнянь з параметрами _________________ 5
Розділ ІІ. Розв’язування нерівностей з параметрами _____________ 12
Список використаних джерел _________________________________ 18
Вступ
Задачі з параметрами - один із найбільш важких розділів елементарної математики. Інтерес до задач з параметрами не випадковий. Теоретичне вивчення фізичних процесів часто приводить до деяких рівнянь або нерівностей, які містять параметри, є необхідною частиною розв’язання таких задач являється дослідження характеру процесу в залежності від значень параметрів.
Якщо нагрівати газ у закритій посудині, т о маса газу буде величиною сталою, а температура і тиск газу – змінними . Якщо нагрівати газ, що знаходиться у посудині закритій поршнем , який може вільно рухатися, то тиск газу і його маса-сталі, атемпература і об’єм- змінні величини. Неважко уявити дослід, коли об’єм буде сталим, а, наприклад, значення тиску у рідині буде змінюватись.
Кажуть, що величина є сталою, якщо вона приймає у даному розгляді одне й те ж саме значення; змінною, якщо вона приймає у даному розгляді різні значення.
Розв'язати задачу з параметрами - це значить встановити для яких значень параметрів задача має розв’язки і знайти ці розв’язки (як правило, в залежності від параметрів). Тобто розв’язування таких задач має супроводжуватись дослідженням.
Для розв’язування задач з параметрами не вимагається ніяких спеціальних знань, які виходять за рамки шкільної програми. Однак, розв’язування задач з параметрами вимагає глибоких знань властивостей елементарних функцій, властивостей рівнянь і нерівностей. Крім того, при використанні графічних методів треба вміти виконувати побудови різних графіків, вести графічне дослідження.
Оскільки задачі з параметрами дуже різноманітні, то їх розгляд в даній роботі буде обмежено в основному розв’язуванням типових задач.
РОЗВ’ЯЗУВАННЯ РІВНЯНЬ, НЕРІВНОСТЕЙ ТА СИСТЕМ З ПАРАМЕТРАМИ.
Звичайно в рівняннях, нерівностях, системах буквами позначають невідомі величини, але іноді рівняння, нерівність, система крім таких букв містить ще букву, яка позначає невідоме стале число - параметр.
Тоді ми маємо справу не з одним рівнянням, або нерівністю, або системою, а з їх нескінченною кількістю, які дістаються при різних значеннях параметра. При цьому може статися так, що при деяких значеннях параметра рівняння, нерівність або система не має розв’язків, при деяких має єдиний розв’язок, при деяких - безліч тощо.
Розв’язати рівняння (нерівність, систему) означає для кожного значення параметра встановити, чи має рівняння (нерівність, система) розв’язки; якщо так, то встановити ці розв’язки, які в більшості випадках залежать від параметра.
На жаль, універсальних методів розв’язування задач із параметрами немає. Найбільш загальну схему розв’язування можна окреслити наступним чином: спочатку знаходять область допустимих значень параметра (якщо вона відрізняється від множини всіх дійсних чисел), потім цю множину розбивають на випадки, в кожному з яких відповідь одна й та сама (наприклад, рівняння не має розв’язків або розв’язок виражається одним і тим самим виразом через параметр).
Зауважимо, що важливим етапом розв’язування задач з параметрами є запис відповіді, особливо для рівнянь (нерівностей, систем), розв’язування яких, розгалужується (містить декілька випадків) залежно від значень параметра. У відповіді до таких задач збираємо всі раніше отримані результати, зазвичай записуючи їх у формі
«якщо..., то...».
Розділ І. Розв’язування рівнянь з параметрами.
Розв’язати рівняння
1)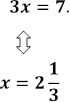 2)
2) 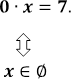 3)
3)
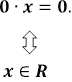
Розв’язання рівняння ax=b зводиться до розв’язання трьох систем:
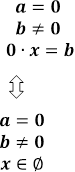
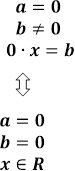
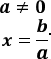 або
або
або
або
|
|
|
Вид рівняння |
Розв’язання |
|
|
1) |
|
|
|
2) |
|
|
|
|
3) |
|
|
|
Розв'язування більш загального параметричного рівняння:
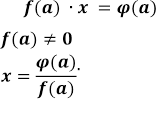
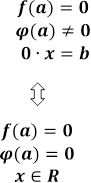
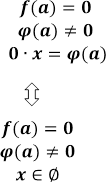 зводиться до
розв'язування трьох систем.
зводиться до
розв'язування трьох систем.
або або

1) 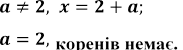 При
При
2) При
Розв’язати рівняння
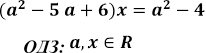
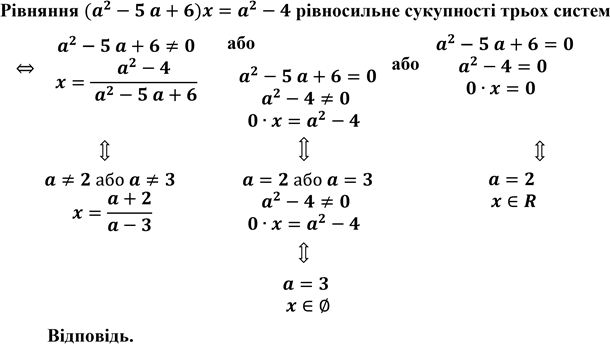
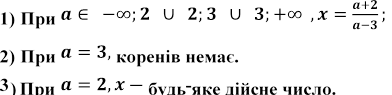
Розв'язання
рівняння ![]()
зводиться до розв'язування трьох систем.
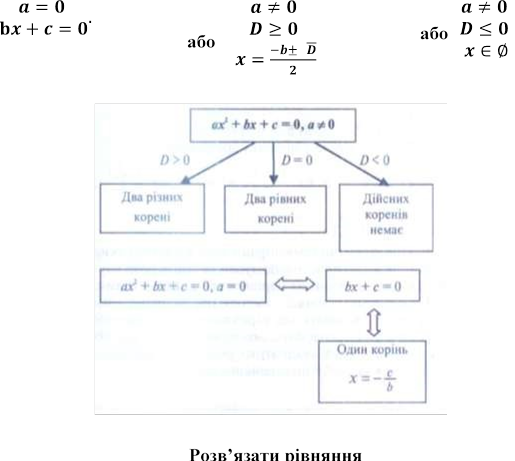
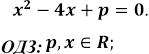
D=16-4p.
Рівняння рівносильне сукупності двох систем
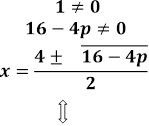 або
або 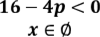
![]()
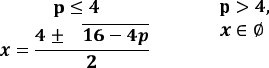
Відповідь.
1) При
2) 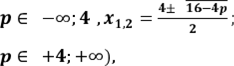 При дійсних
коренів немає.
При дійсних
коренів немає.
Розв’яжіть рівняння 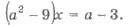
Розв’язання. При розв’язуванні рівняння слід розглянути випадки, коли a2 - 9 = 0 (де відбувається, коли а = 3 або а = -3) і коли 2 - 9 ≠ 0. Отже:
а
1) а = 3, тоді рівняння матиме вигляд 0 ∙ х = 0 і х — будь-яке число;
2) а = -3, рівняння матиме вигляд 0 ∙ х = -6 і рівняння не має розв’язків;
3)
а ≠ 3; а ≠ -3, тоді ![]()
Відповідь. Якщо а = 3, то х — будь-яке число; якщо а = -3, то рівняння не має розв’язків; якщо а ≠ 3; а ≠ -3, то х = 1/(a + 3).
Розв’яжіть рівняння ах2 - 2х - 1 = 0.
Розв’язання. Якщо параметр а = 0, то матимемо лінійне рівняння, якщо ж а ≠ 0, то квадратне. Такі випадки і слід розглянути.
1) а = 0; -2х - 1 = 0; х = -0,5.
2) а ≠ 0. Знаходимо дискримінант рівняння D = 4 + 4а. Якщо D ≥ 0, тобто 4 + 4а ≥ 0; а ≥ -1, то рівняння матиме два кореня (за умовою, що
а ≠ 0), різні або однакові:
![]()
Якщо ж 4 + 4а < 0, тобто а < -1, то рівняння не матиме дійсних коренів.
Відповідь. Якщо а = 0, то х = -0,5; якщо а < -1, то рівняння не має
розв’язків; якщо а ≥ -1 і а ≠ 0, то ![]()
Розв’язати відносно х:
![]()
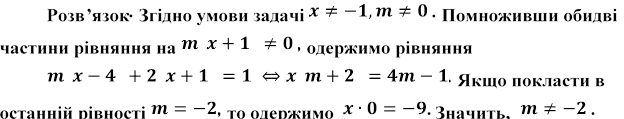
Провіримо, чи існують такі значення т , для яких знайдене
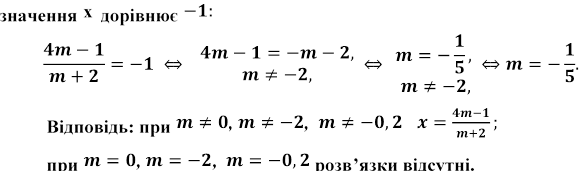
При яких
дійсних значеннях параметра корені рівняння 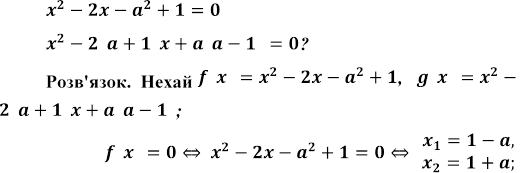 лежать між
коренями рівняння
лежать між
коренями рівняння
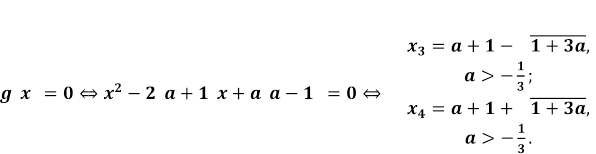
З малюнка слідує що
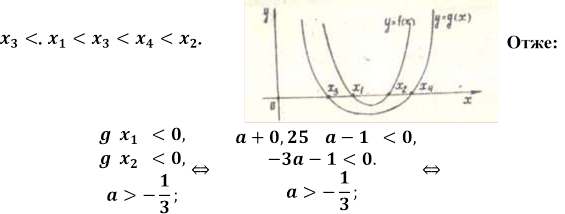
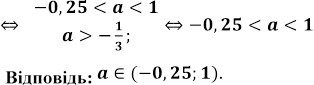 .
.
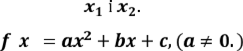 Часто в задачах виникає питання про
умови знаходження заданого дійсного чиcла відносно нулів квадратичної функції
Часто в задачах виникає питання про
умови знаходження заданого дійсного чиcла відносно нулів квадратичної функції
Мають місце слідуючі твердження:
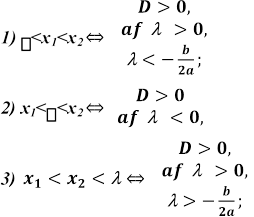
Знайти всі значення параметра m, яких
один корінь рівняння ![]() від’ємний, а
другий ― більший 5.
від’ємний, а
другий ― більший 5.
Розв'язок. Розв'язання задачі зводиться до розв'язання систем нерівностей:
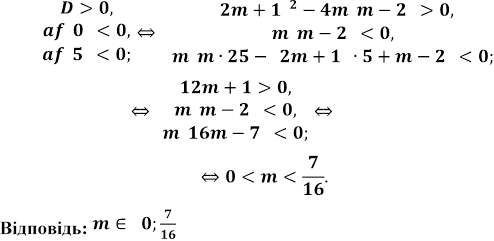
Розділ ІІ. Розв’язування нерівностей з параметрами.
Розв’язати нерівності 1)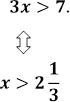 2)
2)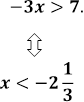 3)
3) 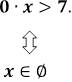
|
4) |
5) |
3) |
|
|
|
|
|
|
|
|
Розв’яжіть нерівність: ах ≤ 2.
Розв’язання. При розв’язуванні нерівності слід розглянути випадки а < 0, а = 0, а > 0.
1)
а < 0. Поділимо ліву і праву частини нерівності на
число а. Оскільки а < 0, то при діленні на від’ємне число знак
нерівності змінюється на протилежний. Маємо x ≥ ![]() .
.
2) а = 0. Маємо 0 ∙ х ≤ 2, х — будь-яке число.
3)
а > 0. Поділимо ліву і праву частини нерівності на
число а. Оскільки а > 0, то приділенні на додатне число знак
нерівності не змінюється. Маємо x ≤ ![]() .
.
Відповідь. Якщо
а < 0, то ![]() ; якщо а = 0,
то х — будь-яке число; якщо а > 0, то х ≤
; якщо а = 0,
то х — будь-яке число; якщо а > 0, то х ≤ ![]() .
.
Розв'язування нерівності:
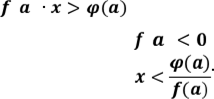 зводиться до
розв'язування трьох систем.
зводиться до
розв'язування трьох систем.
або
або
![]()
Розв’язати нерівність
![]()
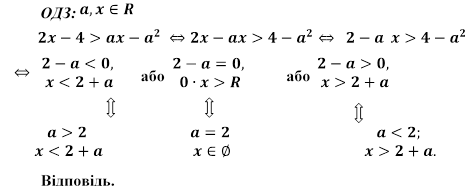
1)
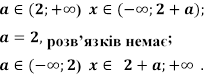 При
При
2) При
3) При
Розв’язати нерівність
![]()
![]() ОДЗ:
ОДЗ:
Нерівність рівносильна сукупності трьох систем:
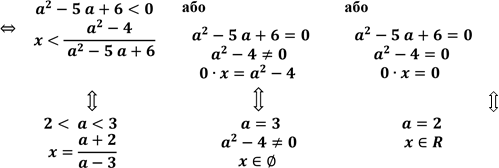
Відповідь.
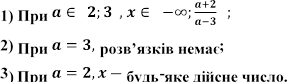

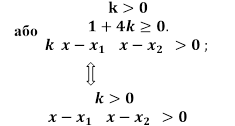
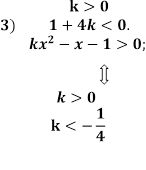
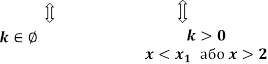
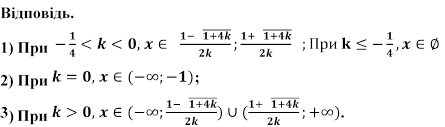
Знайти всі
значення параметра a при яких кожен розв’язок нерівноcті ![]() задовольняе нерівності
задовольняе нерівності ![]() .
.
Розв’язок.
Введемо позначення: ![]() .
Для виконання умов
.
Для виконання умов
задачі квадратний тричлен має два корені, які лежать на проміжку
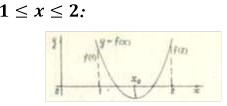
Знайдемо дискримінант D тричлена і абсцису вершини параболи
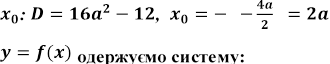 . Користуючись графіком функції
. Користуючись графіком функції
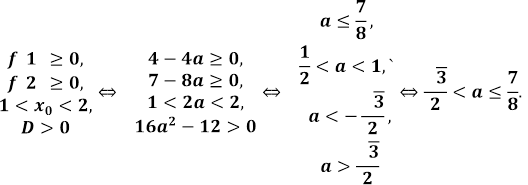
Відповідь: ![]()
Для кожного дійсного значення параметра a розв'язати нерівність
![]()
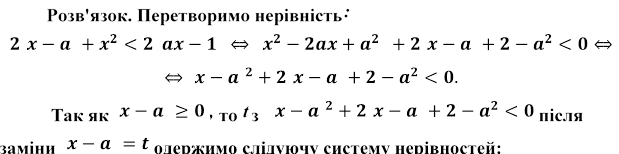
![]()
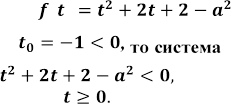 Оскільки
вітки параболи напрямлені
Оскільки
вітки параболи напрямлені
вгору, а абсциса її вершини
буде мати
розв'язок лише в тому випадку, якщо більший корінь рівняння ![]() додатній.
додатній.
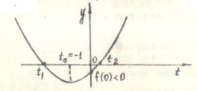
Це має місце при виконанні умов:
![]()
3. Розв’язування систем з параметром
Розв’яжіть систему рівнянь
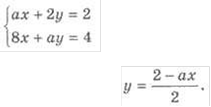 Розв’язання.
З першого рівняння маємо Підставимо у
Розв’язання.
З першого рівняння маємо Підставимо у
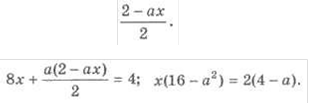 друге рівняння замість у
вираз
друге рівняння замість у
вираз
Отримаємо
Далі, якщо а = 4, то х ∙ 0 = 0,
х — будь-яке число, а ![]() якщо а = -4, то 0 ∙ х = 16, рівняння,
а тому й початкова система не має розв’язків.
якщо а = -4, то 0 ∙ х = 16, рівняння,
а тому й початкова система не має розв’язків.
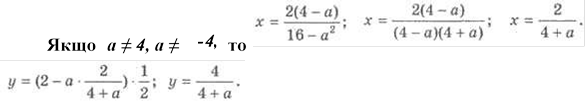 Тоді
Тоді
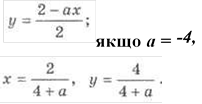 Відповідь. Якщо а = 4, то
х - будь-яке число;
Відповідь. Якщо а = 4, то
х - будь-яке число;
то система не має розв’язків; якщо а ≠ 4, а ≠ -4, то
При дослідженні систем двох лінійних рівнянь з двома невідомими
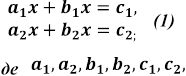 ―
довільні дійсні, числа користуються
―
довільні дійсні, числа користуються
слідуючими твердженнями:
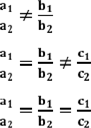 1) якщо , то
система (1) має єдиний розв’язок; 2) якщо , то система (1) не має
розв’язків;
1) якщо , то
система (1) має єдиний розв’язок; 2) якщо , то система (1) не має
розв’язків;
3) якщо , то система (1) має безліч розв’язків.
Знайти всі значення параметрів а і b при яких система
![]() має безліч розв’язків.
має безліч розв’язків.
Розв'язок. Лінійна система має безліч розв’язків, якщо
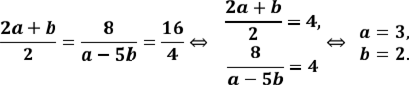
Відповідь: ![]()
Список використаних джерел
1. І. А. Кушнір Шедеври шкільної математики //Київ АСТАРТА 1995. 2. Ш. Г. Горделадзе, М. М. Кухарчук, Ф. П. Яремчук //Збірник конкурсних задач з математики, Вища школа, Київ-1976. 3. П. І. Горштейн, В. Б. Полонський, М. С. Якір //Задачі з
параметрами//Киев, РИА "Текст", МП "ОКО", 1992.
4. Г. В. Апостолова, В. В. Ясінський //Перші зустрічі з параметром. //Факт- 2004.
5. В. Г. Коваленко, В. Я. Кривошеєв, Л. Я. Лемберський //Алгебра 8,
Експериментальний начальний посібник для 8 класу//, Київ, "ОСВІТА", 1995.


про публікацію авторської розробки
Додати розробку
