Урок "Числові функції. Область визначення і множина значень"
Тема заняття: Числові функції. Область визначення і множина значень.
Мета заняття: Повторити і розширити первинні відомості про функції, набуті в основній школі. Розвивати пам'ять, мислення; розвивати цікавість до математики . Виховувати наполегливість, вміння працювати разом.
Тип заняття: лекція комплексного характеру.
Обладнання: підручники, опорні таблиці графіків найуживаніших функцій, презентація «Все про функції».
Література: 1. Алгебра і початки аналізу. Підручник для 10 кл. загальноосвітніх навчальних закладів, М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук. – К.: Зодіак – ЕКО, 2002, - 272 с.
2. Алгебра і початки аналізу: Підручник для 10-11 кл. загальноосвітніх навчальних закладів. – К.: Освіта, 2006. – 255с.
План заняття
I. Організація початку заняття .
II. Актуалізація опорних знань:
- Усне опитування студентів.
- Перевірка виконання домашнього завдання.
III. Мотивація навчальної діяльності, повідомлення теми, мети уроку.
IV. Вивчення нового матеріалу:
- Основні відомості про функцію.
- Область визначення функції.
- Область значень даної функції.
V. Виконання вправ.
VI. Підведення підсумків заняття.
VII. Домашнє завдання.
Хід заняття
I. Організація початку заняття .
II. Актуалізація опорних знань:
1. Питання до усного опитування:
- Які числа називаються цілими? Як позначається множина цілих чисел?
- Як називаються цілі додатні числа?
- Які дії завжди можливі в множині натуральних чисел?
- Що таке відсоткове відношення двох чисел?
- Назвіть три основні види задач на відсотки.
2. Перевірка виконання домашнього завдання.
III. Мотивація навчальної діяльності, повідомлення теми, мети уроку.
Епіграф до заняття:
Функції потрібні не лише натуралістові, без них тепер не обійдеться і соціологія. Взагалі, нині немає жодної галузі людського знання, куди не входили б поняття про функції та їх графічне зображення.
К.Ф. Лебединцев
Одне з найважливіших понять математики – функція. З її допомогою моделюють і досліджують різноманітні процеси, що відбуваються навколо нас. Повторимо основні відомості про функцію, які ви вже знаєте з попередніх класів.
Термін «функція» ввів у математику Г.В. Лейбніц. Видатний німецький вчений. За освітою юрист, працював бібліотекарем, досліджував проблеми мовознавства, хімії, конструював обчислювальні машини. Ввів терміни «абсциса», «ордината», логічну символіку, знаки множення і ділення. «Після Лейбніца , мабуть, уже не було людини, яка повністю охоплювала б усе інтелектуальне життя свого часу» (Н. Вінер)
IV. Вивчення нового матеріалу
Залежність змінної ![]() від
від ![]() називають функцію, якщо кожному значенню
називають функцію, якщо кожному значенню ![]() відповідає значення
відповідає значення ![]() .
.
Зміна ![]() називається незалежною змінною або аргументом функції, а зміна
називається незалежною змінною або аргументом функції, а зміна ![]() – залежною зміною, або функцією.
– залежною зміною, або функцією.
Функції позначають латинськими буквами ![]() або рівністю
або рівністю ![]() .
.
Якщо задане конкретне значення аргументу ![]() то
то![]() називають значенням функції
називають значенням функції ![]() у точці
у точці ![]() .
.
Область визначення позначення ![]() або
або ![]() –визначати) - це множина значень, яких набуває незалежна змінна
–визначати) - це множина значень, яких набуває незалежна змінна ![]() .
.
Значенням функції називають значення змінної ![]() , якою вона набуває за певного значення
, якою вона набуває за певного значення ![]() . Позначаються
. Позначаються ![]() або
або ![]() . (
. (![]() – існувати).
– існувати).
Числовою функцією з областю визначення ![]() називають залежність, згідно з якою кожному числу
називають залежність, згідно з якою кожному числу ![]() із множини
із множини ![]() відповідає деяке єдине число
відповідає деяке єдине число ![]() із множини
із множини ![]() .
.
При знаходженні області визначення слід пам’ятати
-
Розглядаємо функція є многочленом
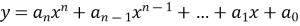 то
то 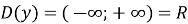
-
Якщо функція має вигляд
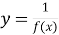 , то слід вважати
, то слід вважати 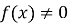 . Чому ?
. Чому ?
-
Якщо функція має вигляд
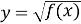 або
або 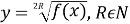 , то слід вважати
, то слід вважати 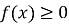 (арифметичний квадратний корінь або корінь парного степеня існує тільки з невід’ємних чисел)
(арифметичний квадратний корінь або корінь парного степеня існує тільки з невід’ємних чисел)
-
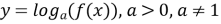 то слід вважати
то слід вважати 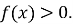
-
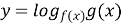 , то
, то 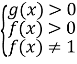
V. Виконання вправ.
1. Для функції ![]() знайти
знайти ![]() Д/з
Д/з ![]()
Розв’язання

2. Для функції ![]() знайти
знайти ![]()
Розв’язання
![]()
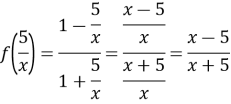
![]()

3. Знайти область визначення функції
-
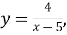 тому
тому 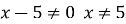 Звідси, область визначення даної функції
Звідси, область визначення даної функції 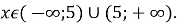
-
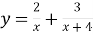 Розв’язком є
Розв’язком є
![]()
Отже ![]() .
.
-
За умови
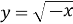
![]() Д
Д![]()
-
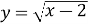 - Д/з
- Д/з
![]() , Д
, Д![]()
VI. Підведення підсумків заняття.
- Що називають функцією? Як позначають функції? Навести приклади.
- Що таке область визначення функції?
- Що таке область значень, або область зміни функції?
- Чи будь – яка формула задає функцію?
VII. Домашнє завдання.
Опрацювати § 1 (п.1), № 1 (1,2,7); № 3 (1,10)


про публікацію авторської розробки
Додати розробку
