Урок "Дійсні числа та дії над ними. Відсоткові розрахунки"

Тема заняття: Дійсні числа та дії над ними. Відсоткові розрахунки.

Мета заняття: Узагальнити і систематизувати знання студентів про дійсні числа, відсотки, нагадати правила виконання дій над дійсними числами. Розвивати логічне мислення студентів, їх пам’ять, мову. Виховувати самостійність, сумлінне відношення до навчання.

Тип заняття: лекція комплексного характеру.

Обладнання: підручники, презентація.

Література:

          1. Руданський Ю.К., Костровій П.П., Мусій Р.С., Веселовський О.В. та інщі. Практикум з елементарної математики. Ч.1.

 2. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенько А.К. Математика

 3. Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу. 10-11 кл.

План заняття

 І. Організація початку заняття.

 II. Актуалізація опорних знань.

 ІІI. Повідомлення теми, мети, плану заняття.

 IV. Вивчення нового матеріалу:

1. Числові множини.
2. Поняття ірраціонального числа, дійсного числа.
3. Поняття відсотку. Відсоткові розрахунки.
4. Дії над дійсними числами.

V. Підведення підсумікв заняття.

VI. Домашнє завдання.

Хід заняття

 І. Організація початку заняття.

 II. Актуалізація опорних знань.

 IІІ. Повідомлення теми, мети, плану заняття.

 IV. Вивчення нового матеріалу.

Поняття числа в історії розвитку математики поступово розвивалося і розширювалося. Спочатку було введено натуральне число і нуль для лічби, потім дробові числа – для вимірювання величин і ділення натуральних чисел. Пізніше у зв’язку з потребами практики і розв’язку рівнянь було введено від’ємні числа (дробові і цілі), які разом із цілими і дробовими додатними числами і 0 утворювали множину раціональних чисел

– множина всіх натуральних чисел

– цілихчисел

–раціональних чисел

– дійсних чисел, числова пряма

У виконують всі 4 дії: «+», «-», «х», «/», крім ділення на нуль.

Відомо, що раціональне число може бути зображеним у вигляді звичайного дробу або у вигляді нескінченного десяткового періодичного дробу, а кожен нескінченний десятковий періодичний дріб зображає певне раціональне число. Зазначимо, що кожний скінчений десятковий дріб можна записати у вигляді нескінченного десяткового дробу, що закінчується нулями.

Дійсні числа .  Числа, які можна подати у вигляді

нескінченого десяткового дробу

Наприклад: 0, 32 = 0, 3200 ... = 0,32 (0).

Якщо ж некінчений десятковий дріб не періодичний, то він не є раціональним числом. Даний дріб є ірраціональним числом. Ірраціональним числом називається нескінченний десятковий неперіодичний дріб.

Раціональні і ірраціональні числа утворюють множину дійсних чисел. Цю множину позначають буквою R.

Таким чином кожне дійсне число зображається у вигляді нескінченого десяткового дробу.

Геометрично дійсні числа зображаються за допомогою точок числової осі (координатної прямої).

Координатна пряма – ця пряма з початковою точкою, вибраним додатним напрямком та одиничним відрізком.

Якщо a < b, то точка а міститься на числовій осі ліворуч від точки b.

При виконанні дій над дійсними числами в практичних задачах їхз замінюють наближеними значеннями.

Наприклад: = 1, 41421 ...

Десятковим наближенням числа з недостачею будуть числа: 1; 1,4; 1,41; 1,414; 1,4141;...

Десятковим наближенням з надлишком будуть такі числа: 2; 1,5; 1,42; 1,415; 1, 4143;...

Модулем числа х називають відстань від початку відліку до точки х. Позначають .

Модуль додатного числа дорівнює цьому числу, а модуль від’ємного числа є протилежне йому число. Модуль нуля – нуль.

   х, якщо х ≥ 0,

             Тобто: =  

   -х, якщо х < 0.

Модуль різниці двох чисел дорівнює відстані між точками, які зображують ці числа.

Рівність = 1 означає, що точка х міститься на відстані 1 від точки 2 : х = 1, х = 3

Нерівність = 3 означає, що точка х міститься від точки 1 на відстані меншій ніж 3, тобто – 4 < х < 2.

Соту частину будь-якої величини або числа називають відсотком (процентом) «%», тобто

Наприклад 1 коп.-1% від грн., 1 см – 1% від метра.

,

Правило 1. Щоб перетворити дане число на відсотки, треба це число помножити на 100

Приклад:

Правило 2. Щоб перетворити дане число відсотків на дріб чи усне число, треба розділити дане число відсотків на 100.

Приклад:

Існують три основні задачі на відсотки:

1. Знаходження відсотків від числа;
2. Знаходження числа за відомими його відсотками;
3. Знаходження відсоткового відношення двох чисел.

1. Щоб знайти число 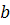, що становить 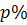від числа 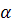, треба число 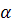поділити на 100 і помножити на число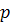, тобто

Щоб знайти відсотки від числа треба ці відсотки записати звичайним чи десятковим дробом і дане число помножити на здобутий дріб

Задача Приклад: Скільки сухої ромашки можна одержати із 25 кг свіжої, якщо вона при сушці втрачає 84% своєї маси ?

1. 100%-84%=16% - залишилося ромашки після сушіння
2. Обчислимо скільки ромашки становить 16 % від 25 кг

16:100=0,16

Відповідь: 4 кг.

2. Знаходження числа за відомими його відсотками

Щоб знайти число за його відсотками, треба відсоток записати у вигляді звичайного чи десяткового дробу і розділити дане число на цей дріб.

Приклад: При помолі пшениці вихід борошна становить 80%. Скільки пшениці треба змолотити, щоб отримати 520 кг борошна?

1. 80%=
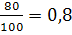
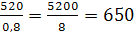2. (кг)

Відповідь: треба змолотити 650 кг пшениці

3. Знаходження відсоткового відношення двох чисел

Щоб визначити відсоткове відношення двох чисел, слід знайти їх відношення і виразити його у відсотках, тобто помножити знайдене відношення на 100 і поставити знак у відсотках.

Приклад: на заваді 40% усіх верстатів перевели на підвищенні швидкості, унаслідок чого продуктивність праці виросла на 30% . На скільки % збільшиться виробництво на заводі

1. 40%=
2. 
3. 

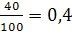
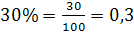
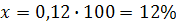
Відповідь: на 12%

V. Підведення підсумікв заняття.

1. Як позначаються натуральні числа? Наведіть приклади.

2. Назвіть найменше натуральне число. Чи існує найбільше натуральне число?

3. Сформулюйте означення раціонального числа. Як позначається множина раціональних чисел?

VI. Домашнє завдання.

Обчислити значення виразу: