Урок: "Побудова графіків функцій за допомогою геометричних перетворень".

Тема: Побудова графіків функції за допомогою геометричних перетворень

Мета: закріпити навички побудови графіків функцій за допомогою геометричних перетворень; розвивати увагу, пам'ять, логічне мислення, комунікативні навички; виховувати працелюбність, самостійність

Тип заняття: лекція комплексного характеру.

Обладнання: підручники, презентація «Графіки функцій».

Література:Афанасьєва О.М., Бродський Я.С., Сліпенко А.К., математика (підручник для студентів ВНЗ І-ІІ р.а. технічних спеціальностей) К.: Вища школа, 2001.

План заняття

І. Організація початку заняття.

ІІ. Актуалізація опорних знань:

1. Перевірка домашнього завдання.
2. Усне опитування студентів.

ІІІ. Вивчення нового матеріалу

IV. Підведення підсумків заняття.

V. Домашнє завдання

Хід заняття

І. Організація початку заняття.

ІІ. Актуалізація опорних знань

• Дати відповідь на запитання:

1. Що таке функція ?
2. Що називається графіком функції ?
3. Які функції ви знаєте ? Яким способом вони задаються ?

ІІІ. Вивчення нового матеріалу

Розглянемо найбільш розповсюдженні функції

Лінійна функція та її графік

Функція, задана формулою де -деякі числа, називають лінійною. Область визначення функції є множина всіх дійсних чисел . Графіком лінійної функції є пряма. Для побудови графіка достатньо знайти координати двох точок цього графіка. Взявши – точки перетину з віссю . Взявши - точка перетину з віссю .

yy

                0                            хx

Приотримано пряму , яка паралельна осі і співпадатиме з віссю , якщо

             у                                                                           у

           в                                                                                    у=0

                                           х                                                                      х

Функціяназивається прямою пропорційною, де -кофіціент пропорційності. Графік є пряма, яка проходить через початок координат

                                                            у                                                              

при

при

                                                                                          х

Розглянемо функції , які входять у коли , .

Функція. Графіком є пряма лінія, яка проходить через початок координат.

у

                                              х

Властивості :

1. Д

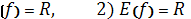
3) нулі функції при (функція має тільки один нуль в початку координат

4) зростає на всій області визначення

5) функція не має ні мінімуму, ні максимуму

6) – функція  – непарна, її графік симетричний відносно початку координат.

Функція

1. спадає по всій області визначення

Функція і іі графік

Називають оберненою пропорційною

Д{0}.

Графіком є гіпербола. Якщо , то вітки гіперболи розташовані в І і ІІІ координатних кутах, якщо , то у ІІ і IV координатних кутах.

При отримуємо рівнобокі гіперболи.

Властивості:

А) Д{0}

Б) {0}

В) Функція не має нулів, оскільки рівняння не має коренів

Г) Функція спадає при , а також при

Д) мін і мах не має

Е) непарна

Є) графік функції не перетинає вісь , але при необмеженому наближенні до осі , ніде її не перетинаючи.

Квадратична фікціяі іі графік де авс – задані числа .

Д. Графіком є парабола. Якщо , то вітки параболи напрямлені вгору; якщо – то вниз.

Функція– це парабола, вершина якої збігається з початком координат, а вітки спрямовані вгору

Властивості:

1. Д
2. 
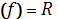
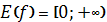
3. має 1 нуль при
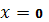
4. приймає + знак при 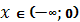v(0;+)
5. ,
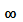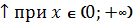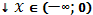
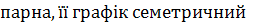6. відносно осі

Функція– це кубічна парабола

Властивості:

1. Д
2. 
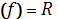
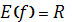
3. має 1 нуль при
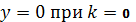
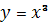4. приймає – знак при 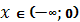, + при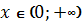
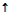5. на всій області визначення
6. непарна, лише відносно початку координат

Функція таїї графік

Властивості:

1. Д
2. 
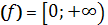
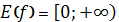
3. має 1 нуль 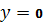при
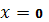
4. приймає лише + знак
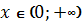
5. функція 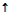при
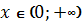
6. функція має мін при 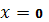, мін .
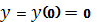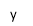7. ні парна, ані непарна

Функція

Непарна зростаюча Д(f)=R, E(f)=R

Функція

Ця функція визначається так

Визначено при , приймає лише + значення

Функція

y

3

2

1

                                                     3    2   1    0    1    2     3     4

-1

-2

-3

Функція

                                   1

-3       -2       -1       0       1       2       3       х

IV. Підведення підсумків

V. Домашнє завдання

Пр. 1, пит..18-23,25,26, №3(1,4,7,10)