Урок "Розв’язування вправ. Контрольна робота з теми "Функції, їх властивості та графіки ""

Тема заняття: Розв’язування вправ. Контрольна робота.

Мета заняття: перевірити якість засвоєння студентами основних понять і властивостей теми, виявити рівень вмінь і навичок застосування їх на практиці; розвивати пізнавальну активність студентів, логічне мислення, розвивати техніку обчислень, творчу та розумову активність, виховувати впевненість у своїх силах, самостійність; виховувати пізнавальний інтерес до предмета, позитивну мотивацію до навчання, швидкість реакції.

Тип заняття: комбінований

Обладнання: тестові завдання.

Література:

1. Алгебра і початки аналізу. Підручник для 11 кл. загальноосвітніх навчальних закладів, М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук. – К.: Зодіак – ЕКО, 2002, - 272 с.

2. Алгебра і початки аналізу: Підручник для 10-11 кл. загальноосвітніх навчальних закладів. – К.: Освіта, 2006. – 255с.

План

I. Організація початку заняття.

II.  Актуалізація опорних знань:

1) перевірка домашнього завдання;

2) фронтальне усне опитування;

3) тестування.

III. Контрольна робота

IV. Підведення підсумків заняття.

V. Домашнє завдання.

Хід заняття

I. Організація початку заняття.

II.  Актуалізація опорних знань

1) контрольні запитання до теми функції,їх властивості та графіки:

• Що таке функція?
• Яка функція називається зростаючою?
• Яка функція називається спадною?
• Яка функція називається парною? Яка непарною?
• Яка функція називається оберненою?

2) тестові завдання

1 варіант

1. Функція задана формулою . Тоді дорівнює:

2. Областю визначення функції є:

3. Нулями функції у = х² – 8х + 16 є:

4. Серед наведених графіків зазначте графік функції .

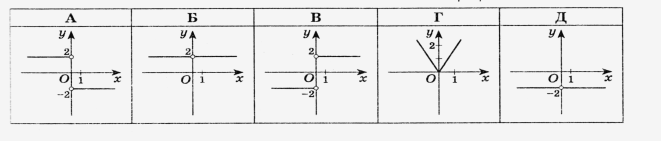5. Непарною є функція:

6. Для побудови графіка функції у=(х+1)³, необхідно виконати:

Завдання 7 передбачає встановлення відповідностей.

До кожного рядка, позначеного ЦИФРОЮ доберіть один рядок, позначений БУКВОЮ і поставте позначки у бланку відповідей на перетині відповідних рядків (цифри) і колонок (букви).

7. Встановіть за графіком функції її основні властивості.

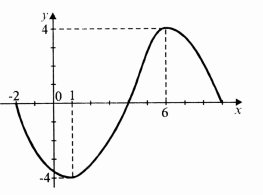
1. Функція зростає на:                                А. (-2; 4)

2. Функція спадає на:                                  Б. (-2; 6)

3. f(x)>0 на:                                                  В. (1; 6)

4. f(x)<0 на:                                                  Г. (-2; 1)(6; 9)

                                                                      Д. (4; 9)

            А       Б       В        Г        Д

2 варіант

1. Функція задана формулою . Тоді дорівнює:

2. Областю визначення функції є:

3. Нулями функції є:

4. Серед наведених графіків зазначте графік функції .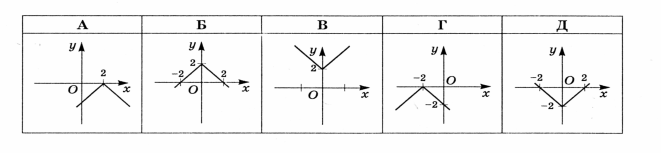5. Парною є функція:

6. Для побудови графіка функції у=2х² необхідно виконати:

Завдання 7 передбачає встановлення відповідностей.

До кожного рядка, позначеного ЦИФРОЮ доберіть один рядок, позначений БУКВОЮ і поставте позначки у бланку відповідей на перетині відповідних рядків (цифри) і колонок (букви).

7. Встановіть за графіком функції її основні властивості.

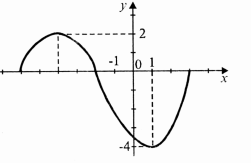
1. Функція зростає на:                                А. (-6; 3)

2. Функція спадає на:                                  Б. (-2; 3)

3. f(x)>0 на:                                                  В. (-4; 1)

4. f(x)<0 на:                                                  Г. (-6; - 4)(1; 3)

                                                                      Д. (-6; -2)

            А       Б       В        Г        Д

Відповіді

III. Контрольна робота

IV. Підведення підсумків.

V. Домашнє завдання

Виконати завдання протилежного варіанту з тестових завдань.

Контрольна робота з тами: «Функції, їх властивості та графіки»

           1 варіант                                                               2 варіант                                       

1. Знайдіть значення функції:

    у точках 1; -1; 3.                                            у точках 5; 14; 30.

Відповідь: f(1)=0;  f(-1)=2;  f(3)=2/3.                                       Відповідь: f(5)=0; f(14)=3; f(30)=5

2. Знайдіть область визначення функції :

а)                                                  а)  ;         

Відповідь: D(у)=(-;-2][l;+)                         Відповідь: D(y)=(-∞;-4]U[-3;+∞).

б)                                                              б)

Відповідь: D(у) = [3;+).                                          Відповідь: D (y)=

3. Дослідіть на парність і непарність функцію

                                 Розв’язання:

а) Через те, що D(f)=R i

-непарна.

б)  Через те, що D(f)=R i

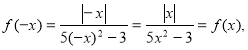то    парна.

4.  Побудуйте в одній системі координат графіки функцій:

;