Урок "Числовые множества". Урок №6

Урок № 6         § 14

Тема: Числовые множества.

Цель урока:

Образовательная: ознакомить с числовыми множествами, дать учащимся определение рациональных и иррациональных чисел, ввести понятие действительных чисел.

Развивающая:  развивать вычислительные навыки и умение работать с приближенными значениями.

Воспитательная: воспитание аккуратности и любознательности.

Тип урока: урок усвоения новых знаний и умений

Оборудование: мел, доска, карточки с заданием (с итогами самостоятельной работы).

Х о д   у р о к а

1. Организационный момент.

- проверка готовности класса к уроку;

- проверка готовности учащихся к уроку;

- приветствие

  Итоги самостоятельной работы (раздать карточки).

  Анализ домашней работы:

  Два  ученика у доски готовят № 429(1,2), № 429(3,4).

  В это время № 432 – просмотреть у всех учащихся.

2. Мотивация урока.

Не нужно нам владеть клинком,
Не ищем славы громкой.
Тот побеждает, кто знаком
С искусством мыслить тонким.

Г. Уордсворт.

Сегодня на уроке, ребята, нам предстоит выполнить серьёзную работу. От вас потребуется усидчивость, стремление, внимание, последовательность и правильность выполнения заданий.

3.Объяснение нового материала

  Актуализация материала. В пятом классе вы изучали натуральные числа. Это числа, которые используют для счета: 1; 2; 3; 4; ... . Все натуральные числа образуют множество натуральных чисел. Это множество обозначают буквой N.

Коротко это записывают так: N={1; 2; 3; 4;...}.

Кроме множества натуральных чисел существуют и другие числовые множества.

Натуральные числа, противоположные им числа и число нуль образуют множество целых чисел. Это множество обозначают буквой Z.

Коротко это записывают так: Z = {... - 3; - 2; - 1; 0; 1; 2; 3; ...}.

Известные нам числа - целые и дроб­ные, положительные и отрицательные - представляют собой множество рацио­нальных чисел  (обозначают буквой Q).

Рациональными их на­зывают потому, что каждое можно записать в виде частного, отношения двух целых чисел, а слово «отношение» на латинском языке - ratio.

 Из курса предыдущих классов вы знаете, что любое число можно представить в виде обыкновенной дроби, а те в свою очередь в виде бесконечной периодической дроби т.е.

  .

 Таким образом, можно сказать, что

каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби;

и

любая бесконечная периодическая десятичная дробь изображает некоторое рациональное число.

 А существуют ли числа, отличные от рациональных?  Да  существуют. Можно доказать, например, что и т.д. невозможно представить в виде обыкновенных дробей. т.е. в виде бесконечной периодической десятичной дроби. Вычисляя значения  получаем бесконечные непериодические десятичные дроби. Так

  = 1,4142135...,    = 1,7320508…,    = 4,472135…,

  = 3,1622776...,       = 3,1415926…

 где - отношение длины произвольной окружности к ее радиусу.

  Эти числа не рациональные и мы их назовем иррациональными.

(латинское  ir  соответствует отрицательной частице  не).

Доказательство иррациональности числа вы можете прочитать на стр. 122  нашего учебника в рубрике «Открытие иррациональности».

Иррациональные числа вместе с рациональными образуют множество действительных чисел.

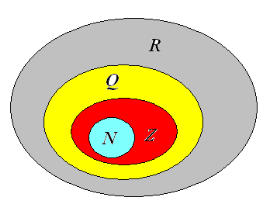  Множества натуральных, целых, рациональных и дей­ствительных чисел обозначают соответственно буквами

N, Z, Q, R. Каждое из этих множеств  явля-
ется подмножеством (частью) следую-
щего множества.  Любое натураль-

ное число является одновременно и
целым, и рациональным, и действитель-
ным. Любое целое число — также рацио-

нальное и действительное.

N Z Q R

  Действительные числа, записанные в виде бесконечных десятичных дробей, сравнивают по тому же правилу, что и десятичные дроби. Например, число 3,131313...  меньше, чем  число 4,0111...,  и меньше чисел  3,25 и , но больше, чем числа 3,1222..., -2 и 0.

  Действительные числа можно складывать, вычитать, умно­жать, возводить в степень и делить (на числа, отличные от нуля). Для сложения и умножения этих чисел верны переместительный, сочетательный и распределительный законы. Все правила действий над выражениями с переменными, доказанные ранее для рациональных значений переменных, справедливы и для произвольных действительных значений этих переменных. В частности, для любых действительных чисел верны известные вам свойства пропорций, дробей, сте­пеней.

4.  Физкультурная пауза.
         Почти 90% всей информации человек воспринимает глазами. Если устают глаза, снижается наше внимание и активность. Давайте перед следующей задачей дадим отдых глазам и себе.
1. Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 3-4 раза.
2. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3—4 раза.
3. Медленно наклоняйте голову: вперед—влево— вправо -  назад. Повторите 3-4 раза.
4. Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубокий вздох и медленный выдох.

5. Закрепление изученного материала.

    Разминка – устные упражнения №443, №444, №446 - работает весь класс.

  Три ученика у доски выполняют  №448, 453(1,4), 453(2,3,5) – повторив преобразование дробей и закрепив сравнение действительных чисел.

 Следующий ученик выполняет №455

6. Подведение итогов урока. Рефлексия.

• С какими новыми числами и понятиями ознакомились?
• Трудным ли для тебя был материал урока?
• На каком из этапов урока было труднее всего?
• На каком из этапов урока было легче всего?
• Что нового ты узнал на уроке? Чему научился?
• Работал ли ты на уроке в полную меру сил?

7.Домашнее задание  § 14,  № 445, 449, 450, 454.