Урок "Ділення з остачею і способи його графічного моделювання"

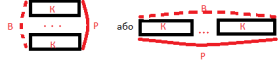
Завдання 1

Вч: Побудуйте величину за формулою : Р : К = В

Д: Нам потрібна мірка К.

Вч: Прошу!

Робота дітей :

   ( схема 1)

Завдання виконується індивідуально.

Мірка відмічається значком ▲ або діти домовляються про свій варіант.

Вч: Як діяли? Що потрібно зробити , щоб побудувати величину за формулою?(Потрібно точно прочитати формулу . В даному випадку : У величині Р мірка К поміщається В разів).

Завдання 2.

На дошці формула:

А : К = В ( ост. М)

Вч: Що змінилось?

Д:Добавилась остача.Тобто величину поділили на частини , отримали В частин і ще остачу. Або : у величині А мірка К поміщається В разів і залишається “кусочок” М. Крім того, величина тепер не Р, а А.
Вч: Чому величина позначена іншою буквою?

Д: Бо це інша величина.

Вч: Як змінилась схема?

Д:Потрібно добавити ще остачу М.

Вч: Яку? Будь-яку? (Чому?)

Д: Так.

Ні. Не будь-яку. Вона має бути меншою за мірку К.

Сигнал. Діти закривають очі.

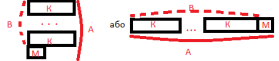
Вч: Змініть схему.

Робота учнів:

(схема 2)Вч: Чи можете ви за допомогою формули розповісти про те, як ви отримали величину А?

Д: А=К*В+М

Вч: Порівняйте 1 і 2 схеми. Це одна і та ж величина?

Д: Різні. Р-це К, взята В разів і ще М.А більше Р.

Завдання 3

На дошці тепер обидві схеми.

Вч: Доберіть числа до 1 схеми( Це завдання швидше виконали ті діти, які здогадались застосувати таблицю множення,- вони написали багато і без помилок).

Вч: А тепер до 2 схеми.

При обговорюванні виявилось № 2 і 5 - обчислювали способом підбору і зробили мало.

Група №3 - ділила парні числа на непарні і навпаки. (Мусить бути остача)

Групи № 1 і 4 - вирішили знову застосувати таблицю. Вони “винайшли” спосіб складання прикладів на ділення з остачею, застосовуючи табличні значення множників і добутку.
Д:Таким способом за одним прикладом на множення, наприклад   6x4=24 можна скласти кілька прикладів на ділення з остачею .

Свої дії діти доповнили схемами:
Після обговорення групи прийшли до такої формули запису способу пошуку числа

(24+1) 25(1)

(24+2) 26(2)

(24+3) 27:6=4(ост. 3)

(24+4) 28(4)

(24+5) 29(5)

Вч: Як складали приклад?

Д: З “кінця” … Ось як :

6+4+ост.=ділене

Аналізуючи величину остачі, учні прийшли до висновку, що найбільшу кількість прикладів на ділене з остачею можна отримати використовуючи таблицю множення на 9, бо при діленні на 9 можливі остачі від 1 до 8 .

В загальному виді не можна записати формулою:

9а+1                 1
9а+2:9=а( ост.2)

9а+3                 3

9а+4                 4

Вч: Чи можна за допомогою моделі розповісти про те, як складати приклади з остачею, користуючись таблицею множення?

Один із варіантів (складений на уроці ):

а- ділене , яке можна змінити за формулою

а=вxс+d, де вxс - табличні данні, d - остача.

Вч: Остача може бути будь-яка?

Д:Ні.Остача має бути меншою за дільник

Мета завдання: дослідити залежність між дільником і остачею.

Гуртова робота.

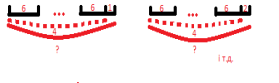
Схеми показують ,якою може бути остача :

Якщо 6x4=24, то 24:6=4,

Якщо 6x4+1+25, то 25:6=4(ост.1)

Обчислення підбору чисел до заданої схеми переходить в обговорення того, як складати приклади на ділення з остачею взагалі ( або : як навчити інших складати такі приклади).

Контрольний момент-

Величина остачі!
Вчитель пропонує помилковий приклад:

30:6=4 (ост. 6), вимагаючи у дітей кожен раз аргументувати свою згоду або непогодження з ним.

Модель може бути результатом як групової, так і фронтальної роботи.