Урок. Дослідження функції за допомогою похідної. Використання похідної
УРОК 33
Тема уроку: Розв'язування вправ.
Мета уроку: Формування умінь учнів досліджувати функції (за допомогою похідної), будувати її графік.
І. Перевірка домашнього завдання.
 Перевірити правильність виконання домашніх завдань за записами, зробленими на дошці до початку уроку.
Перевірити правильність виконання домашніх завдань за записами, зробленими на дошці до початку уроку.
№ 5. 2) у = 1 – 2х2 – ![]() . (рис. 71)
. (рис. 71)

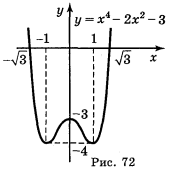 4) у = х4 - 2х2 - 3 (рис. 72)
4) у = х4 - 2х2 - 3 (рис. 72)

II. Формування умінь досліджувати функції (за допомогою похідної) та будувати її графік.
Приклад 1. Дослідіть функцію f(x) = xex та побудуйте її графік.
Розв'язання
1) D(f)=R.
2) Знаходимо абсцису точки перетину графіка функції з віссю ОХ: xex = 0;
х = 0.
Знаходимо ординату точки перетину графіка функції з віссю ΟΥ: у = 0 · е° = 0.
3) Функція неперіодична, ні парна, ні непарна.
4) Знаходимо похідну: f'(x) = (xex)' = x' · ex + x·(ex)'= ex + xex = ex(1+ х).
 D(f ') = R. Знаходимо стаціонарні точки:
D(f ') = R. Знаходимо стаціонарні точки:
f'(x) = 0; ex(x + 1) = 0; х + 1 = 0; х = -1.
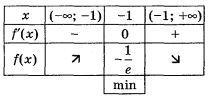
5) Складаємо таблицю.
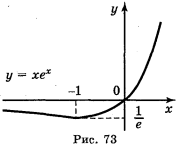
6) Використовуючи результати дослідження, будуємо графік функції у = хеx (рис. 73).
 Приклад 2. Дослідіть функцію
Приклад 2. Дослідіть функцію ![]() та побудувати графік цієї функції.
та побудувати графік цієї функції.
Розв'язання
1) D(y) = (0; +![]() ).
).
2) Знаходимо абсцису точки перетину графіка функції з віссю ОХ:
![]() , lnх = 0; х = 1.
, lnх = 0; х = 1.
Точок перетину графіка функції з віссю ΟΥ немає.
3) Функція неперіодична, ні парна, ні непарна.
4) Знаходимо похідну: ![]() =
=![]() .
.
D(y') = (0; +![]() ). Знаходимо стаціонарні точки:
). Знаходимо стаціонарні точки:
у' = 0; ![]() =0; 1 – ln x = 0; ln x = 1; х = е.
=0; 1 – ln x = 0; ln x = 1; х = е.
5) Складаємо таблицю:
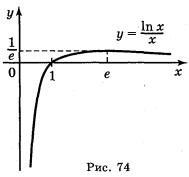
 6) Використовуючи результати досліджень, будуємо графік функції у =
6) Використовуючи результати досліджень, будуємо графік функції у = ![]() (рис. 74).
(рис. 74).
Виконання вправ
1. Побудуйте графіки функцій, дослідивши функції:
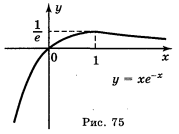
а) у = xe-x·, б) у = ![]() ; в) y =
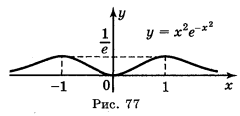
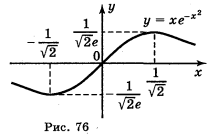
; в) y =![]() ; г) у =
; г) у = ![]() .
.
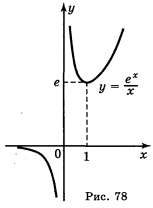 Відповідь: а) рис. 75; б) рис. 76; в) рис. 77; г) рис. 78.
Відповідь: а) рис. 75; б) рис. 76; в) рис. 77; г) рис. 78.
2. Дослідіть функції та побудуйте їхні графіки:
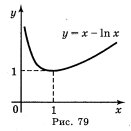
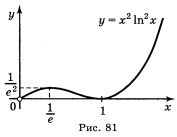
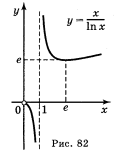
а) у = х - ln х; б) у = 2lnх -х2; в) у = x2ln2x; г) у = ![]() .
.
Відповідь: а) рис. 79; б) рис. 80; в) рис. 81; г) рис. 82.
III. Підведення підсумків уроку.
IV. Домашнє завдання.
Підготуватися до тематичної контрольної роботи. Розділ VIII § 5.
Вправа № 5 (5; 7).



про публікацію авторської розробки
Додати розробку
