Урок "Довжина кола й дуги кола"

Урок 4.

Тема уроку. Довжина кола й дуги кола

Мета уроку: Виведення формул для знаходження довжини кола та довжини дуги кола. Формування вмінь учнів  застосовувати виведені формули  до розв’язування задач.

Тип уроку: комбінований.

Наочність і обладнання: підручник, презентація PowerPoint

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашнього завдання          (Слайд 3)

ІІІ. Сприйняття і усвідомлення нового матеріалу

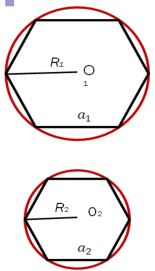
Уявимо, що коло зроблено з тонкого дроту. Якщо його розрізати в деякій точці А і розпрямити, то одержимо відрізок АА₁, довжина якого і є довжиною кола.

(Слайд 4)

Периметр будь-якого правильного вписаного в коло многокутника є наближеним значенням довжини кола. Чим більше число сторін такого многокутника, тим точніше це наближення, оскільки многокутник при збільшення сторін все ближче і ближче «прилягає» до кола.

Теорема.                                                                                                                        (Слайд №5)

Відношення довжини кола до його діаметра  одне  й те  саме  для кожного кола. 

Історична довідка                                                                                                               (Слайди 6,7,8)

Число π математична константа, що визначається у Евклідовій геометрії як відношення довжини кола до його діаметра.

Число π виникло в геометрії як відношення довжини кола до довжини його діаметра, проте воно з'являється і в інших областях математики. Вперше позначенням цього числа грецькою літерою π скористався британський математик Джонс (1706), а загальноприйнятим воно стало після робіт Ейлера. Це позначення походить від початкової букви грецьких слів περιφέρεια — оточення, периферія та περίμετρος — периметр.

Діаграми обчислення числа π Архімедом

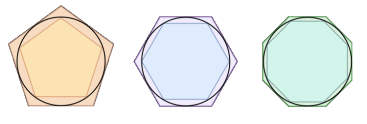
 Архімед, можливо, першим запропонував метод обчислення π математичним способом. Для цього він вписував у коло і описував біля нього правильні багатокутники. Приймаючи діаметр кола за одиницю, Архімед розглядав периметр вписаного багатокутника як нижню оцінку довжини кола, а периметр описаного багатокутника як верхню оцінку. Таким чином, для шестикутника виходить                      

Розглядаючи правильний 96-кутник, Архімед отримав оцінку

• Вчені завжди намагались обчислити число π з максимально можливою точністю.

   Так, наприклад, у 1949 році за допомогою комп'ютера ENIAC було обчислено число π до 2037 знаків, а в 1995 — вже 4.294.960.000 знаків.

• В багатьох університетах США відзначається   День π, який припадає на 14 березня, тобто у американській формі запису дат на 3/14.
• Слюсарчук Андрій Тихонович, український нейрохірург, доктор медичних наук, професор, у червні 2009 року він встановив  світовий рекорд, запам'ятавши 30 мільйонів знаків числа π , які були надруковані у 20-ти томах тексту.
• У серпні 2009 року японські вченні обрахували число π з точністю до 2 трильйони 576 мільярдів 980 мільйонів 377 тисяч 524 знаків після коми .

(Натиснувши на прізвище вченого, можна ознайомитися з його портретом)

(Слайд 9)

(Слайд 10)

(Слайд 11)

IV. Закріплення й осмислення нового матеріалу

Розв’язування вправ                                                                                                               (Слайд12, 13)

V. Домашнє завдання                                                                                                 (Слайд 14)

Опрацювати  §12.

Практична робота №8* .

Завдання 13

20; 11(в); 24(б); 31*

VI. Підсумок уроку                                                                                                        (Слайд 15)

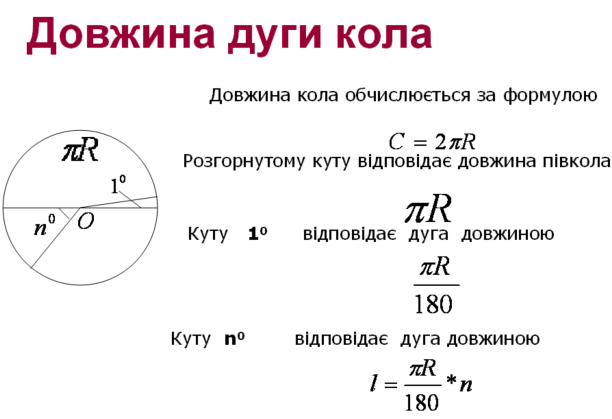
1. Чому дорівнює відношення довжини кола до діаметра?

2. Запишіть формули для знаходження довжини кола; довжини дуги кола, що відповідає куту n⁰.

3. Знайдіть довжину кола радіусом 2 см.