Урок. "Функціонально залежні величини. Тестові завдання у форматі ЗНО"

МАТЕМАТИКА

ТЕМА:

ФУНКЦІОНАЛЬНО ЗАЛЕЖНІ ВЕЛИЧИНИ

Тестові завдання у форматі зно

Суббота Олена Олександрівна, викладач математики Білозерського професійного гірничого ліцею

СПЕЦІАЛІСТ ВИЩОЇ КАТЕГОРІЇ

y 2x2 7x

2x2 7x 0;

x(2x 7) 0;

Нулі функції, це такі значення аргументна x при яких зазначення функції дорівнює нулю (y = 0)

1 0; або 2x 7 0; 2x 7 :2;

x 2; x2 3,5.

y f (x),  f (x) f (x) x 2; x 2

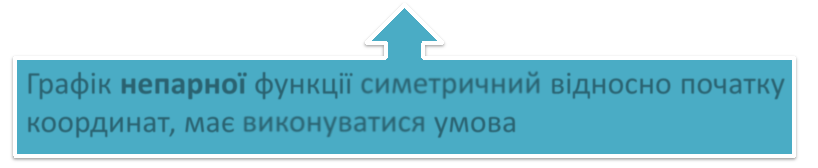
Графік непарної функції симетричний відносно початку координат, має виконуватися умова

A y x4 парна Б y x4 1парна

y(2) (2)4 16 y(2) (2)4 116117 y(2) 24 16              y(2) 24 116117 y(2) y(2)              y(2) y(2)

В y x3 1непарна ні непарна Г y x3 непарна y(2) (2)3 1817              y(2) (2)3 8 y(2) 23 1819              y(2) 23 8

y(2) y(2)

Д

y(2) y(2) y x2 1 парна

y(2) (2)2 1413 y(2) 22 1413 y(2) y(2)

y 4

Тоді для y 2x 4 2x

x 2 x 2

y

4 y 4 3 y 3 2 y 2 1 y 1

0 2 x

y 2x

4 y 4

A y 2x Б y x

2x 0 x 0

В y x

D(y) (; )

x 2 (1) D(y) [0; )

x 2

D(y) (; 2]

Г y x 2 Д y x 2 x 20                      x 20

x 2 x 2

D(y) [2; ) D(y) [2; )

A y x4 x В y x4 парна Г y x3 непарна

y(2) (2)4 (2) 162 18 y(2) 24 2 162 14

y(2) y(2)

y(2) (2)4 16 y(2) 24 16

y(2) y(2)

y(2) (2)3 8 y(2) 23 8

y(2) y(2)

Б y x4 x Д y(2) (2)3 1817

y(2) (2)4 (2) 162 14 y(2) 24 2 162 18

y(2) y(2)

y(2) 23 1819

y(2) y(2)

5x 3y 11,

2x 5y 23;

5 25x 15y 55, 3 6x 15y 69;

31x  124 124

31 x 4

543y 11 3y 1120

3y 9

Відповідь (4; 3) y 3

3 f (x) 

x3 1 x2 x 1

(3)3 1          271 (3)2 (3)1     931

1 f (x) x2 x 9

f (3) (3)2 (3)9 3

4 f (x) 2xx 4 x2 4x 4

2

2 f (x) x 2

f (3) (3)4 94 5

2(3)4 3

3 (3)2 4(3)4

9124 2

12

1. y 3 x b 4 4 6b

1

4 8b 48b

b 12

x;y

2. y 3 x 12

Знайдемо точку перетину з Ox (y 0)

0 3 x 12

3 x 12 : 3 x 124 x 9

y

12 y 3 x 12

Знайдемо точку перетину з Oy (x 0)

y 3 012

y 12 c ?

За

y 12

теоремою Піфагора

c2 x2 y2 0 x 9 9 x

c x2 y2 92 122 81144 225 15 c x y 15912 36

36

3 ymin y(0) 202 1 3

2

y x2 2x 7, якщо y 15 x2 2x 7 15

x2 2x 7150 x x2 2, 1 2, x2 2x 80              x x2 8           x2 4

xmin 1 2

11

x 40,

7x 0;

x 4, x 4, x 7 (1); x 7.

D(y) [4; 7]

4 7

l x2 1 7(

x

4)74 11