Урок геометрії, 10 клас "Рухи і перетворення в просторі"

Урок геометрії, 10 клас

Тема: Рухи і перетворення в просторі

Мета: Повторити поняття рух, поширити його на просторову систему координат, навчити учнів читати перетворення простору за зміною координат точки.

Обладнання: картки, опорний конспект , презентація, геометричні прилади.

Хід уроку

1. Актуалізація опорних знань

a)Бліц –опитування: коротка самостійна робота

Варіант 1

1.Дано точки А(0;-12;0), В(0;4;5),С(7;-7;0), Д(-10;0;20), К(0;0;7). Які з даних точок лежать на площині ХZ, а які – на осі ОУ?

2.Обчислити відстань між точками А(2;-2;13) та В(5;-6;1).

Варіант 2

1.Дано точки А(0;2;3), В(4;0;0),С(0;0;-1), Д(-3;4;0), К(0;5;0). Які з даних точок лежать на площині ХУ, а які – на осі ОZ?

2.Обчислити відстань між точками А(5;-1;7) та В(3;-4;1).

б)Зібрати зошити для перевірки домашнього завдання.

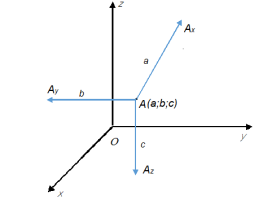2.Сприйняття нового матеріалу.

Евристична бесіда.

1. Поняття перетворення простору.

1. Симетрія;
2. Поворот;
3. Паралельне перенесення;
4. Гомотетія.

2. Перетворення простору, які є рухом:

Симетрія:

1)  відносно координатних площин

А)відносно площини ХОУ рис. 1:

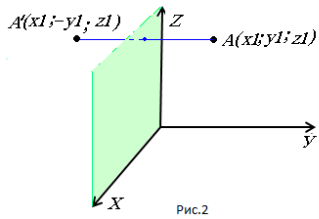
Б) відносно площини ХОZ рис. 2:

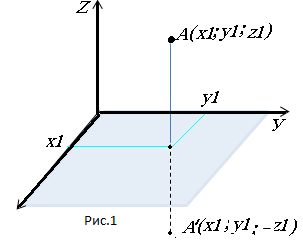B) відносно площини УОZ рис. 3:

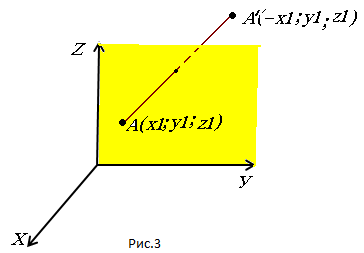
Висновок: при симетрії відносно площини змінюється та  координата, яка не приймає «участі» у назві площини.

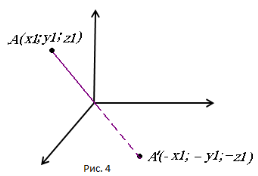
2)При симетрії відносно координатної осі зміни зазнають координати, які не «називають» відповідну вісь.

Наприклад, при симетрії відносно осі ОУ точка А(х1;у1;z1)перейде в точку

А'(-х1;у1;-z1).

3)Симетрія відносно точки:  1)координати точки , відносно якої здійснюють симетрію, є серединою відрізка.

2) (центральна симетрія):

Змінюються всі координати на протилежні

4)Симетрія відносно прямої  (поворот).

1.Поворот  є рух.

2.Поворот площину переводить

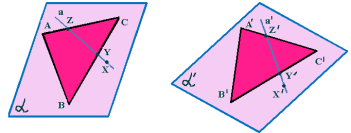у площину.

3.Дві фігури називаються рівними, якщо вини суміщаються рухом.

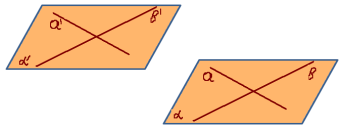
5)Паралельне перенесення

x’=x+a

y’=y+b

z’=z+c

1 Паралельне перенесення є рух.

2. Всі точки зміщуються вздовж паралельних прямих на одну і ту саму відстань.

3.Кожна пряма переходить в паралельну їй пряму (або саму себе).

4.Які б не були точки  А і А’, існує єдине паралельне перенесення, в результаті якого точка А переходить в точку А’.

5.Кожна площина переходить або в себе, або в паралельну їй площину.

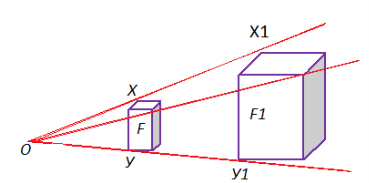3.Гомотетія в просторі.

Гомотетією відносно центра О з коефіцієнтом гомотетії k називають перетворення, яке відображає кожну точку простору Х на Х’ так,що О’Х’= k∙OX.

1)При перетворенні подібності відстані між точками зінюються в одному і тому ж відношенні.

2) Фігури називаються подібними .Коефіцієнт подібності k

4.Закріплення знань, умінь, набуття навичок.

1. Задача №1. Дано точки А(5;4;-9), В(0;-1;2); С(2;-7;-3).Знайдіть точки, симетричні даним відносно координатних площин.
2. Задача №2. Знайдіть координати  точки, гомотетичної точці А(4;6;9) відносно початку координат, якщо коефіцієнт гомотетії а) k =– 3; б) k= 0.5
3. Задача №3 Записати координати  точки А’, в яку переходить точка

  А(-4;12;-13) при виконанні двох послідовних симетрій відносно площин ХОУ та УOZ.

5. Рефлексія.

Контрольні запитання

1.Що таке перетворення симетрії відносно точки? Яка фігура називається центрально-симетричною?
2.Поясніть, що таке перетворення симетрії відносно площини. Що таке площина симетрії фігури?
3.Яке перетворення фігури називається рухом?
4.Доведіть, що рух у просторі переводить площину у площину.
8.Які фігури у просторі називають рівними?
9.Дайте означення паралельного перенесення.
10.Перелічіть властивості паралельного перенесення.
11.Доведіть, що при паралельному перенесенні у просторі кожна площина переходить або в себе, або у паралельну площину.
12.Що таке перетворення подібності? Перелічіть його властивості.
6. Домашнє завдання

1. Опрацювати §15

2.Розв’язати № 252,№253

Список використаної літератури.

1. Бевз Г.П.Геометрія 10-11: підручник для 10-11 класів загальноосвітніх навчальних закладів/Бевз Г.П., Бевз В. Г.,Владімірова Н.Г.- Київ, «Вежа», 2004р.-222.
2. Погорелов О.В.Геометрія:стереометрія, підручник для 10-11 класів середньої школи/ Погорелов О.В. - Київ, «Освіта», 2000р.-129.
3. Капіносов А.М. Геометрія 10 клас:дидактичні матеріали для різнорівневого навчання/ Капіносов А.М. – Дніпропетровськ, видавничо-поліграфічне підприємство «Дніпро»,1993р. -132.