Урок геометрії "Трапеція. Середня лінія трикутника, трапеції."

УРОК № 24                                                                              ДАТА 30.11.2012

Тема уроку. Трапеція. Середня лінія трикутника, трапеції.

Мета уроку: узагальнити та систематизувати вивчений матеріал з теми «Трапеція. Середня лінія трикутника, трапеції»; підготувати учнів до контрольної роботи шляхом розв'язування різнорівневих задач і повторення теоретичного матеріалу.

Тип уроку: узагальнення та систематизація знань.

Хід уроку

I. Організаційний момент

Учитель розподіляє клас на диференційовані групи. У групах вибираються консультанти.

 II. Перевірка домашнього завдання

Консультанти перевіряють наявність домашнього завдання та відповідають членам групи на питання, що виникли.
 

ІІІ. Аналіз самостійної роботи попереднього уроку
 

IV. Актуалізація опорних знань учнів
Групи по черзі ставлять одна одній теоретичні питання з теми цього уроку («карусель»). Під час оцінювання враховуються правильність і швидкість надання відповіді — її треба сформулю­вати протягом 30 секунд.
 

V. Розв'язування задач різного рівня в диференційованих групах
Групи, які розв'язують задачі середнього та достатнього рівнів, записують розв'язання на дошці. їх рецензують учні, які розв'язують задачі високого рівня. Учні, які вже розв'язали задачі високого рів­ня, стають консультантами в групах середнього та достатнього рівнів і пояснюють їм розв'язання своїх задач.

С Задача 1. Тупий кут рівнобічної трапеції на 20° більший від гострого кута. Знайдіть кути цієї трапеції. (Відповідь: 80°, 80°, 100°, 100°.) 

С Задача 2. У рівнобічній трапеції периметр дорівнює 40 см, се­редня лінія — 12 см. Знайти бічну сторону трапеції. (Відповідь: 8 см.) 
 

С Задача 3. У рівнобедреному трикутнику ABC з основою АС, яка дорівнює 12 см, і бічною стороною, що дорівнює 10 см, точки D і Е — середини сторін АВ іВС відповідно. Доведіть, що ADEC — трапеція. Знайдіть її периметр. (Відповідь: 28 см.) 
 

Д Задача 4. Бісектриси кутів при основі трапеції перетинаються на її другій основі. Доведіть, що друга основа дорівнює сумі бічних сторін трапеції.
Доведення
Н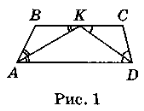ехай ABCD (рис. 1) — дана трапеція (ВС || AD), AK — бісектриса кута BAD. Отже, BAK = KAD. Але оскільки BKA = KAD як внутрішні різносторонні при паралельних прямих ВС і AD і січній АК, то трикутник АВК рівнобедрений з основою АК і АВ =ВК. Аналогічно трикутник KCD рівнобедрений з основою KD i CD = KC. Звідси ВС = ВК + КС = АВ + CD, що й треба було довести. 

Д Задача 5. У рівнобічній трапеції менша основа дорівнює 10 см, бічна сторона — 4 см, а кут між бічною стороною та більшою основою дорівнює 60°. Знайдіть середню лінію трапеції.
Розв'язання
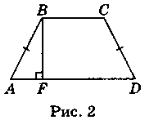
Нехай ABCD (рис. 2) — дана трапеція (AD || BC), AB = CD = 4 см, ВС = 10 см, BC < AD, BAD = 60°. Проведемо висоту BF (BF  AD). У трикутнику ABFAFB = 90°, ABF = 30°. Отже, AF =АВ = 2 см. Оскільки AD = BC + + 2AF, то AD = 10 + 4 = 14 см. Отже, середня лінія цієї трапеції (14 + 10) : 2 = 12 см. 
Відповідь: 12 см.
 

Д Задача 6. Сторона трикутника дорівнює 10 см, а одна із серед­ніх ліній — 6 см. Знайдіть дві інші сторони трикутника, якщо периметр даного трикутника дорівнює 30 см.
Розв’язання
За теоремою про середню лінію трикутника одержуємо, що сто­рона, яка лежить проти даної середньої лінії, дорівнює 12 см, тоді третя сторона трикутника: 30 – (10 + 12) = 8 см.
Відповідь: 8 см. 
 

В Задача 7. Основи трапеції дорівнюють 6 см і 20 см. Знайдіть довжину відрізка, який сполучає середини діагоналей трапеції.
Розв'язання
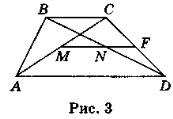
Нехай ABCD (рис. 3) — дана трапеція з основами AD = 20 см і ВС = 10 см, точки М і N — середини діагоналей АС і BD відповід­но. У трикутнику ACDпроведемо середню лінію MF, паралельну AD. Оскільки точка М — середина АС, то за теоремою Фалеса точка M — середина BD. Тоді MN належить MF. MF=AD = 10 см. Оскільки точка N — середина BD, а точка F — середина CD, то NF — середня лінія трикутника BCD і NF= ВС = 3 см. Отже, MN = = MF –NF = 10 – 3 = 7 (см).
Відповідь: 7 см. 
 

В Задача 8. Основи трапеції дорівнюють а і b. Визначте довжину відрізків, на які ділить більшу основу пряма, що проходить через середину однієї з бічних сторін паралельно другій бічній стороні трапеції.
Розв'язання
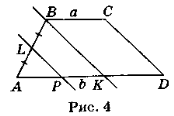
Нехай ABCD (рис. 4) — дана трапеція, у якій AD || ВС, AD = b, ВС = а. Точка L — середина АВ, LP || CD.Проведемо пряму ВК, пара­лельну стороні CD. Отже,LP || ВК. Оскільки точка L — середина АВ, то за теоремою Фалеса АР = = РК. Оскільки ВК || CD, ВС || KD, то чо­тирикутник KBCD — паралелограм і KD = ВС = а . Звідси АР = , PD = .

Відповідь: ; .
  
 VI. Підбиття підсумків уроку
Учитель ще раз звертає увагу учнів на основні теоретичні факти, використані під час розв'язування задач, просить консультантів оцінити роботу всієї групи в цілому та окремих учнів.
 

VII. Домашнє завдання. Повторити всі способи розвьязання задач. Виконати завдання за збірником:№165,166,168