Урок геометрії у 8 класі "Властивості та ознаки паралелограма. Самостійна робота"

Перегляд файлу

УРОК №4

Тема уроку. Властивості та ознаки паралелограма

Мета уроку:

Навчальна:

узагальнити та систематизувати поняття паралелограма, його ознак та властивостей;
закріпити уміння учнів використовувати властивості та ознаки паралелограма до розв’язування задач.

Розвиваюча:

формувати чіткі вміння працювати за готовими рисунками;
застосовувати властивості та ознаки паралелограма під час розв'язування задач різного рівня складності;
розвивати уміння правильно розподіляти час та цінувати кожну хвилину;
розвивати вміння самостійно застосовувати знання до вирішення практичних завдань;

Пізнавальна:

формувати вміння самостійно виконувати роботу;
розпізнавати використання тієї чи іншої властивості чи ознаки в задачі.

Виховна:

виховувати акуратність при побудові малюнків;
виховувати уважність, зібраність при виконанні самостійної роботи;
виховувати інтерес до наукової творчості;

Цілі уроку:

Учні повинні знати:

означення паралелограма, властивості та ознаки паралелограма;

Учні повинні вміти:

правильно розподіляти час при виконанні самостійної роботи;
самостійно застосовувати знання до вирішення практичних завдань та реально оцінювати отриманий результат.

Тип уроку: узагальнення та систематизація знань.

Обладнання: набір демонстраційного креслярського приладдя; слайди до уроку ; мультимедійний пристрій, НКК.

Методи, прийоми, форми роботи: слово вчителя, інтерактивні вправи - робота в групах, вправа «Розминка», вправа «Зорові образи»,вправа «Дослідники»,вправа «Коло двох».

Хід уроку

I. Організаційний момент.Забезпечення емоційної готовності до уроку.

Слово вчителя.

Дорогі діти, сьогодні на уроці ви повинні бути:

У – уважні!

Р – розумні!

О – організовані!

К – кмітливі!

То хто ж із вас хоче бути уважним? Хто розумним і організованим? А хто ж – кмітливим? Ось і побачимо!

II. Перевірка домашнього завдання

Методична ремарка

Наявність домашнього завдання перевіряють консультанти груп. Двоє учнів виконують на дошці малюнки до домашніх задач та їх коротке розв'язання.

Орієнтована відповідь.

Задача 1.Розв'язання

Оскільки сторони паралелограма відносяться як 3:4, то в умові йдеться про сусідні сторони паралелограма. Тоді їхні довжини можна позначити 3х і 4х. Враховуючи те, що протилежні сторони паралелограма є рівними, а його периметр дорівнює 2,8 м, одержимо: (3х + 4х) · 2 = 2,8; 7х = 1,4; х = 0,2. Таким чином, сторони паралелограма дорівнюють 3 · 0,2 = 0,6 (м) і 4 · 0,2 = 0,8 (м).

Відповідь: 0,6 м; 0,6 м; 0,8 м; 0,8 м.

Рис 1 - на дошці

Рис – на дошці.

Задача 2.Доведення

Оскільки за умовою OAD = ОСВ, а вони внутрішні різносторонні при прямих ВС і ADі січній АС, то ВС || ADза ознакою паралельності прямих. Звідси ОВС = ODAяк внутрішні різносторонні при паралельних прямих ВС і ADі січній BD. Розглянемо трикутники ВОС і DOA. У них BO = ODза умовою, ВОС = AODяк вертикальні і OBC = ODA(доведено вище). Отже, ∆BOC= ∆DOAза стороною і двома прилеглими до неї кутами. Звідси випливає, що ВС = AD. Таким чином, у чотирикутнику ABCDпротилежні сторони рівні і паралельні, отже, ABCD— паралелограм за ознакою.

Робота в групах – по рядах. Вправа «Розминка»

Методична ремарка

Поки учні записують на дошці розв'язання домашніх задач, учитель проводить опитування за темами трьох попередніх уроків. Кожній групі пропонується однакова кількість завдань. Повторювати ознаки, названі однією із груп, не можна. Після опитування учні біля дошки пояснюють розв'язання домашніх задач

Закінчіть речення:

За означенням протилежні сторони паралелограма...
Діагоналі паралелограма...
Протилежні сторони паралелограма...
Протилежні кути паралелограма...
Сума кутів, прилеглих до однієї сторони паралелограма...

Назвіть умови, за яких чотирикутник буде паралелограмом.

ІІІ. Формулювання мети і задач уроку. Мотивація навчальної діяльності

1. Слово вчителя. Діти! Сьогодні ви маєте нагоду показати свої знання щодо нашої надзвичайної фігури – паралелограма. Тож, бажаю вам успіхів та натхнення!

IV. Актуалізація опорних знань учні.

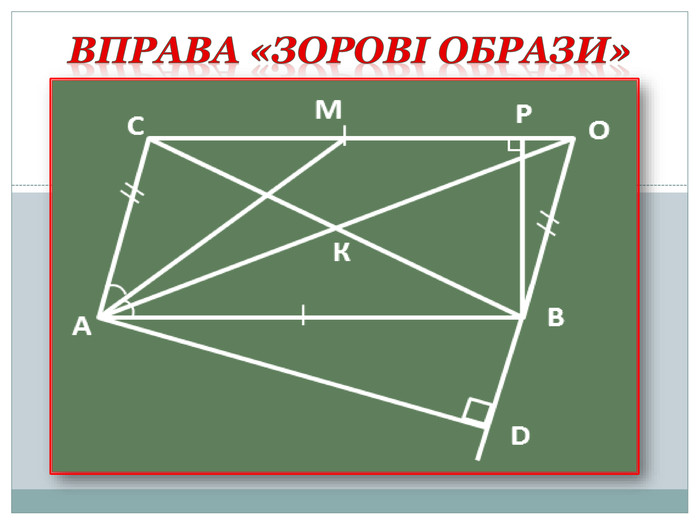
Вправа «Зорові образи» (за готовим рисунком на слайді 1 учні письмово відповідають на запитання вчителя).

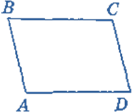
Слайд 1

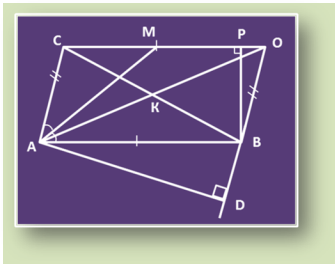який паралелограм ви бачите; ( АСОВ)
відрізок, рівновеликий до відрізка ОС; ( АВ )
який промінь є бісектрисою кута А; ( АМ )
діагоналі паралелограма; ( СВ,АО )
відрізок який є висотою паралелограма, опущеною

на меншу сторону; ( АD )

відрізки рівновеликі до відрізка СК; ( КВ )
відрізок який є висотою паралелограма, опущеною

на більшу сторону; ( РВ )

відрізки, рівновеликі з відрізком СМ; ( СА,ОВ )
кут, рівновеликий куту О; ( А )
кут, рівновеликий куту СВА. ( ОСВ )

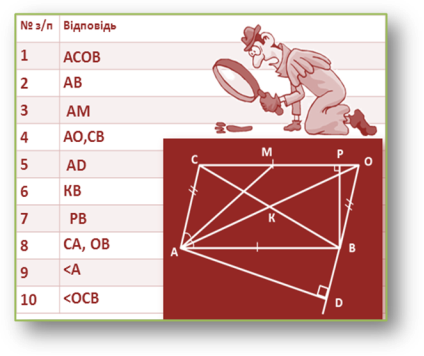
Слово вчителя.

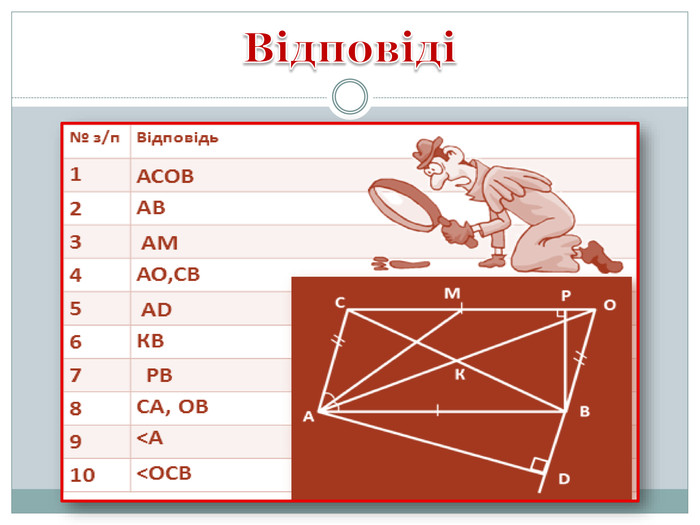
Діти, тепер обміняйтеся аркушами з напарником по парті , перевірте точність відповідей за допомогою слайда 2 та підрахуйте кількість вірних відповідей. Скажіть, хто дав правильну відповідь на всі запитання; на 9; на 8 запитань? Добре.

Слайд 2

V. Закріплення засвоєних навичок і вмінь учнів

Розв’язання задач за готовими рисунками – вправа «Дослідники»

Учням пропонується усно розв'язати задачі за рисунками, заздалегідь підготовленими на дошці. Умови задач теж коротко відображені на дошці.

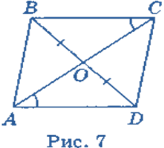
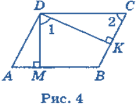
	Задача 1. Дано: ABCD— паралелограм, BMAD, DHBC(рис. 2). Довести: ∆ABM = ∆CDH.
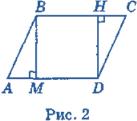
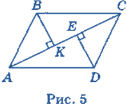
	Задача 2. Дано: ABCD— паралелограм (рис. 3). Довести: ОМ = ОК.
	Задача 3. Дано: ABCD — паралелограм, DMAB, DKBC(рис. 4). Довести: 1 = 2.
	Задача 4. Дано: ABCD— паралелограм, ВК АС, DEAC(рис. 5). Довести: BK = DE.

VІ. Фізкультхвилинка

Виконується за слайдами презентації «І очі скажуть вам спасибі».

VІІ. Самостійна робота

1. Робота в групах – вправа «Коло двох».

Клас поділяється на дві групи, одна виконую тестування за комп’ютером, інша – пише самостійну роботу. Потім учні міняються місцями.

Завдання до І частини – теоретичної – тестування за комп’ютером

Обережно – актинивні кнопки!!!!!!!

Тест на паралелограм

Начало формыЗавдання 1. Паралелограмом називається чотирикутник, у якого протилежні сторони ...

Відповідь:

Паралельні	Перпендикулярні
Рівні	Перетинаються

Завдання 2. В паралелограмі ABCD відрізки AC и BD являються ...

Відповідь:

Суміжними сторонами	Сусідніми сторонами
Протилежними сторонами	Діагоналями

Завдання 3. Дайте назву наступному твердженню: в паралелограмі протилежні сторони рівні.

Відповідь:

Аксіома	Властивість паралелограма
Ознака паралелограма	Означення паралелограма

Завдання 4. Дайте назву наступному твердженню: якщо в чотирикутнику діагоналі перетинаються і в точці перетину діляться навпіл, то це паралелограм.

Відповідь:

Властивість паралелограма	Аксіома
Ознака паралелограма	Означення паралелограма

Завдання 5. Чи правильне наступне твердження: в паралелограмі діагоналі рівні ?

Відповідь:

Завжди не вірно	Інколи вірно, але не завжди
Ніколи не вірно	Завжди вірно

Завдання 6. Чому дорівнює сума всіх внутрішніх кутів в паралелограмі?

Відповідь:

Буває різною

360 градусів

270 градусів

180 градусів

Завдання 7. Чому дорівнює сума довільних двох сусідніх кутів в паралелограмі?

Відповідь:

270 градусів	Буває різною
180 градусів	90 градусів

Завдання 8. Чи являється паралелограм опуклим чотирикутником?

Відповідь:

Завжди не являється	Ніколи не являється
Інколи не являється	Завжди являється

Завдання 9. В чотирикутнику два протилежних кута рівні. Чи являється він паралелограмом?

Відповідь:

Являється	Не являється
Така ситуація неможлива	Не обов’язково

Завдання 10. Чому дорівнює сума градусних мір всіх зовнішніх кутів паралелограма, що взяті по одному при кожній вершині?(2 бали)

Відповідь:

Залежить від паралелограма	360 градусів
340 градусів	180 градусів
270 градусів	450 градусів

Завдання до ІІ частини – практичної – розв’язування задач у зошитах.

Варіант 1

Варіант 2

Завдання 1.

У паралелограмі ABCD сторона АВ дорівнює 3 см, його діагоналі дорівнюють 7 см і 4 см; точка О — точка перетину діагоналей. Чому дорівнює периметр трикутника АОВ?

Завдання 2.

Завдання 1.

У паралелограмі ABCD діагоналі дорівнюють 8 см і 5 см, сторона ВС — 3 см; точка О — точка перетину діагоналей. Чому дорівнює периметр трикутник AOD?

Завдання 2.

У трикутнику ABCА = 50°. Із точки, узятої на стороні ВС, проведено дві прямі, паралельні сторонам АВ і АС. Визначте вид утвореного чотирикутника. Знайдіть його кути.

Із точки, узятої на одній із сторін рівностороннього трикутника, проведено дві прямі, паралельні двом іншим його сторонам. Визначте вид утвореного чотирикутника. Знайдіть його кути.

VІIІ. Підбиття підсумків уроку

Методична ремарка

Учитель відзначає роботу найактивніших учнів; підкреслює необхідність чіткого знання властивостей і ознак паралелограма для подальшої роботи.

Рефлексія.

У мене сьогодні вийшло…
Я зміг…
Я спробував…
Мене здивувало….

IХ. Домашнє завдання

Повторити властивості та ознаки паралелограма.
Розв’язати задачі:

1. Знайдіть сторони паралелограма, якщо його периметр дорівнює 72 см, а одна із сторін у 5 разів менша від другої.

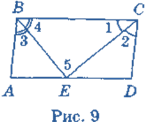
2. Дано: ABCD— паралелограм, 1 = 2, 3 = 4, 3 - 2 = 20° (рис. 9).

Знайти: А.