Урок геометрії у 8 класі "Властивості паралелограма"

УРОК № 2

Тема уроку: Властивості паралелограма

Мета уроку:

 

Навчальна:

• забезпечити засвоєння нового матеріалу, розуміння основних понять.
• познайо­мити учнів з властивостями паралелограма.

Розвиваюча:

• розвивати інтелект учнів, уміння аналізувати, порівнювати, робити умовиводи.
• формувати первинні вміння застосовувати властивості паралелограма під час розв'язування задач різного рівня складності.

Пізнавальна:

• формувати вміння роботи в групах;
• за рисунком та символічним позначенням паралелограма визначати помилки на готових зображеннях;
• розпізнавати використання тієї чи іншої властивості в задачі.

Виховна:

• виховувати інтерес до математики, акуратність при побудові малюнків.
• виховувати зібраність, самовладання, уміння працювати в колективі;
• дотримуватися правил ТБ при роботі за комп’ютером.

 

Цілі уроку:

Учні повинні знати:

• означення паралелограма;
• властивості паралелограма;

Учні повинні вміти:

• логічно аргументувати та формулювати висновки, чітко будувати свою відповідь.
• за рисунком та символічним позначенням паралелограма визначати помилки на готових зображеннях;
• застосовувати властивості паралелограма під час розв'язування задач.

 

Тип уроку: засвоєння нових знань.

Обладнання: набір демонстраційного креслярського при­ладдя; слайди до уроку ; мультимедійний пристрій, НКК.

Методи, прийоми, форми роботи:  слово вчителя, інтерактивні вправи:вправа «Закінчи речення»,вправа «Обернене твердження»,робота в групах -«Знайди помилку»,технологія«Дерево рішень»,дослідження – аналіз,вправа «Продовжи речення».

 

Хід уроку

І. Організаційний момент

Забезпечення емоційної готовності до уроку.

Слово вчителя.

Треба разом привітатись:

- Добрий день! (граючі відповідають)

Дружно, голосно сказати:

- Добрий день!

Вліво, вправо поверніться,

- Добрий день!

Туди-сюди посміхніться:

- Добрий день!

 

ІІ. Перевірка домашнього завдання

1. Робота біля дошки.

Двоє учнів на дошці записують розв'язання завдань 1 і 2, а в цей час з класом виконується вправа «Закінчи речення».

• Чотирикутник являється паралелограмом, якщо його діагоналі….
• Чотирикутник являється паралелограмом, якщо його протилежні сторони…
• Чотирикутник являється паралелограмом, якщо дві його протилежні сторони…
• Чотирикутник являється паралелограмом, якщо його кути…
• Які саме кути?
• Діагоналі чотирикутника АВКМ перетинаються. Чи обов'язково цей чотирикутник є паралелограмом?
• Яка додаткова умова повинна виконуватись, щоб являвся?

 

ІІІ. Формулювання мети і задач уроку.Мотивація навчальної діяльності

1.Слово вчителя.Діти, сьогодні ми у нашої надзвичайної фігури – паралелограма – відкриємо нові можливості – його властивості, бо вони часто використовуються для розв’язання задач.

 

IV. Актуалізація опорних знань учнів

 

1.Вправа – «Обернене твердження»

Учитель пропонує учням сформулювати твердження, обернені ознакам паралелограма.

1.                У паралелограмі діагоналі перетинаються і точкою перетину ді­литься навпіл.
2.                Протилежні сторони паралелограма рівні і паралельні.
3.                Протилежні кути паралелограма рівні.
4.                Далі вчитель пропонує учням пригадати означення паралелогра­ма та допомагає виходячи з нього сформулювати властивість кутів паралелограма, прилеглих до однієї сторони: сума кутів паралело­грама, прилеглих до однієї сторони, дорівнює 180°.

V.Вивчення нового матеріалу

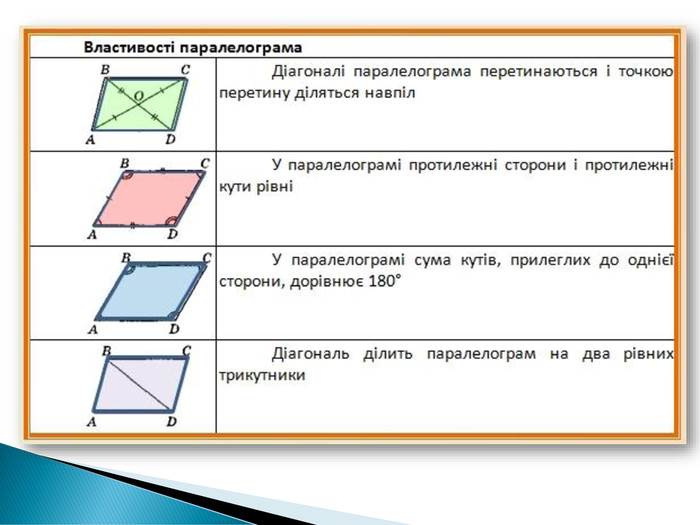
1.Слово вчителя.Давайте узагальнимо  сказане, використовуючи таблицю , яка відображена на слайді.

       Слайд  1

 

Властивості паралелограма
	Діагоналі паралелограма перетинаються і точкою перетину діляться навпіл
	У паралелограмі протилежні сторони і протилежні кути рівні
	У паралелограмі сума кутів, прилеглих до однієї сторони, дорівнює 180°
	Діагональ ділить паралелограм на два рів­них трикутники

 

2.Доведення властивостей.

2.1. діагоналей паралелограма.

Методична ремарка

 Для доведення властивості діагоналей паралелограма вчитель використовує наступну ідею: будує чотирикутник, у якому діагоналі свідомо перетинаються і точкою перетину діляться навпіл, і доводить, що цей чотирикутник збігається з початковим паралело­грамом.

2.2. сторін і кутів паралелограма.

Учні працюють у парах чи невеликих групах, до складу яких входять учні з однаковим рівнем підготовки. Групам, які складаються із більш слабких учнів, учи­тель пропонує довести, що сума кутів, прилеглих до однієї сторони паралелограма, дорівнює 180°, а групам, які складаються із більш сильних учнів,— властивості протилежних сторін і протилежних кутів паралелограма. За необхідності вчитель допомагає «слабким» групам.

Учитель звертає увагу класу на доведену і

застосовану власти­вість діагоналів паралелограма і

просить її сформулювати.

(Діагональ ділить паралелограм на два рівних трикутники.)

VІ. Фізкультхвилинка

Виконується за слайдами презентації «І очі скажуть вам спасибі».

VІІ. Первинне закріплення нових знань учнів

1. Робота в групах.

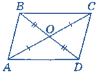
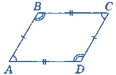
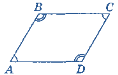
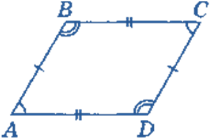
І група виконує вправу «Знайди помилку»(усно за рис.1, зображеним на дошці).

 

 

 

 

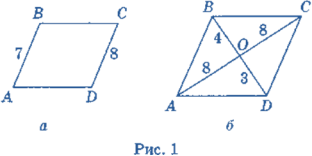
        Рисунки – на дошці

 

 

 

 

ІІ група учнів отримує тестові завдання за комп’ютером та розв’язує їх.

Тестові завдання до вправи «Знайди помилку»(у вигляді окремої презентації)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Розв’язання задач за технологією «Дерево рішень». Робота біля дошки та в зошитах.

Учні розв’язують задачу по черзі, один(з першого ряду) виконує малюнок до задачі, другий(з другого ряду) – записує умову задачі, третій – її розв’язання(складає рівняння), четвертий – розв’язок рівняння, запис висновку та відповідь. Записи відображаються на дошці кольоровою крейдою.

 

 

Задача 1.  Периметр паралелограма дорівнює 56 см. Знайдіть його сторони, якщо одна з них на 6 см більша за іншу.

Розв'язання   Нехай х см (х > 0) — довжина  сторони АВ паралелограма, тоді (х + 6) см — довжина сторони ВС. Враховуючи, що периметр паралелограма дорівнює 56 см і протилежні сторони паралелограма рівні, одержимо рівняння: 2(х + х + 6) = 56; 2х + 6 = 28; 2х = 22; х = 11.   Отже, АВ = 11 см, тоді ВС = 11 + 6 = 17 (см). Відповідь: 11 см, 11 см, 17 см, 17 см.

 

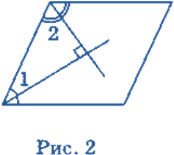
Задача 2. Доведіть, що бісектриси кутів паралелограма, при­леглих до однієї сторони, перетинаються під прямим кутом.

Доведення Оскільки сума кутів, прилеглих до однієї сторони паралелограма, дорівнює 180°, а бісектриси ділять кожний із цих кутів навпіл, то в утвореному трикутнику (рис. 2) 1 +2 = 90°. Таким чином, кут між бісектрисами дорівнює 180°-90° = 90° , що й треба було довести.

 

 

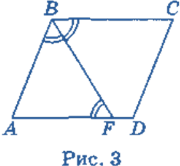
Задача 3.  Бісектриса тупого кута В паралелограма ABCDділить сторону ADна два відрізки — AFі FD(AF>FD), різниця довжин яких дорівнює 2 см. Знайдіть сторони паралелограма, якщо його периметр дорівнює 32 см.

Розв'язання Оскільки ABCD(рис. 3) — паралелограм, то ВС || AD, BF— січна при прямих ВС і AD. Отже, CBF = BFAяк внутрішні різносторонні при паралельних прямих і січній. Тоді трикутник ABF— рівнобедрений з основою BF, оскільки ABF = AFB. Нехай FD= х см (х > 0),тоді AF = АВ = (х + 2)см, AD = AF+ FD= 2х + 2(см). Враховуючи те що в паралелограмі протилежні сторони рівні і його периметр за умо­вою дорівнює 32 см, одержимо рівняння:   2(2х + 2 + х + 2) = 32; 3х + 4 = 16; 3х = 12; х = 4. Таким чином, АВ = CD= 4 + 2 = 6 (см), AD = BC = 2· 4 + 2 = 10 (см). Відповідь: 6 см, 6 см, 10 см, 10 см.

 

 

 

  

 

VIІІ. Підбиття підсумків уроку

1. Дослідження – аналіз.

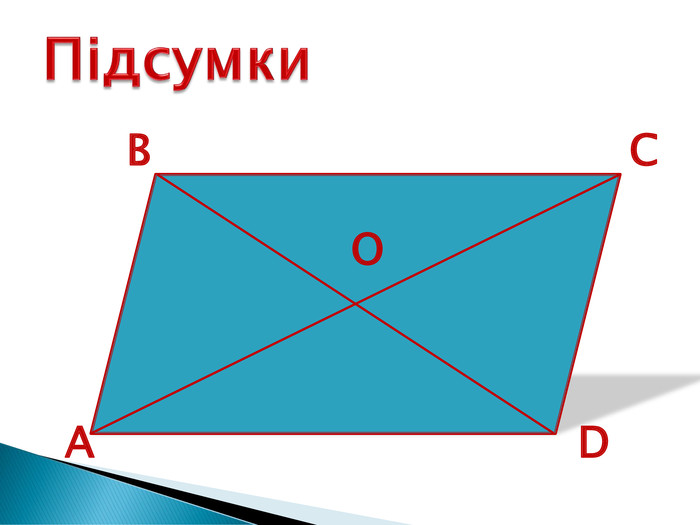
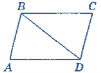
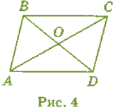
На рис. 4   ABCD— паралелограм.

• Чому дорівнює відрізок АО, якщо діагональ АС дорівнює 12 см?
• Чому дорівнює діагональ BD, якщо відрізок ВО дорівнює 3 см?
• Доведіть, що OD— медіана трикутни­ка ACD.

 

2. Рефлексія - вправа «Продовжи речення».

Я сьогодні дізнався про…..

 

IХ.Домашнє завдання

1. Вивчити властивості паралелограма. Повторити його ознаки.
2. Розв’язати задачі: