Урок геометрії у 8 класі "Властивості та ознаки паралелограма"
Подана робота представляє собою розробку 3-го уроку з циклу уроків з повним дидактичним забезпеченням навчальної теми «Паралелограм» курсу геометрії 8 класу.
- До уроку 3.pptx pptx
- Картки до уроку3.docx docx
- УРОК3.docx docx
Графічний ланцюжок. У будь-якому паралелограмі:1) усі сторони рівні;2) протилежні сторони рівні;3) протилежні кути рівні;4) діагоналі рівні;5) точка перетину діагоналей є рівновіддаленою від двох сусідніх вершин. Чотирикутник є паралелограмом, якщо у нього:6) дві сторони рівні;7) протилежні сторони рівні;8) діагоналі перетинаються;9) діагоналі перетинаються і точкою перетину діляться навпіл. Якщо в чотирикутнику:10) протилежні сторони рівні, то точка перетину його діагоналей є рівновіддаленою від протилежних вершин;11) діагоналі точкою перетину діляться навпіл, то його сусідні сторони рівні;12)дві протилежні сторони рівні і паралельні, то його діагоналі рівні.
Ключ
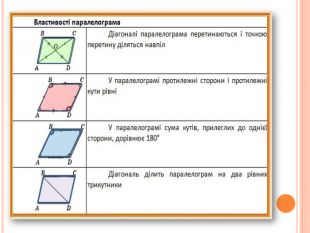
Картки до етапу «Закріплення знань, умінь та навичок»
|
|
|
|
Задача 3.
У паралелограмі ABCD на двірівні частини.
|
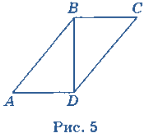
Задача 4. Периметр паралелограма дорівнює 90 см(рис. 5), його гострий кут дорівнює 60°. Діагональ паралелограма ділить його тупий кут у відношенні 1:3. Знайдіть сторони паралелограма.
|
УРОК № 3
Тема уроку. Властивості та ознаки паралелограма
Метауроку:
Навчальна:
- закріпити поняття паралелограма;
- повторити означення паралелограма, його ознаки та властивості;
Розвиваюча:
- формувати в учнів загально навчальні вміння: культуру мовлення, чіткість і точність думки, логічність мислення, здатність відчувати красу ідеї, методу розв'язання задачі;
- формувати чіткі вміння застосовувати властивості та ознаки паралелограма під час розв'язування задач різного рівня складності;
Пізнавальна:
- розпізнавати використання тієї чи іншої властивості чи ознаки в задачі.
Виховна:
- виховувати акуратність при побудові малюнків, уважність, зібраність, спостережливість;
- виховувати сумлінність, здатність до переборення труднощів, працелюбство, уміння працювати в групі.
Цілі уроку:
Учні повинні знати:
- означення паралелограма;
- властивості та ознаки паралелограма.
Учні повинні вміти:
- аналізувати навчальний матеріал, умову задачі, хід розв’язання задач;
- логічно аргументувати та формулювати висновки, чітко будувати свою відповідь;
- застосовувати властивості та ознаки паралелограма під час розв'язування задач різного рівня складності.
Тип уроку: формування вмінь і навичок учнів.
Обладнання:набір демонстраційного креслярського приладдя; слайди до уроку ; мультимедійний пристрій ; картки.
Методи, прийоми, форми роботи: слово вчителя, інтерактивні вправи: вправа «Графічний ланцюжок», робота в групах.
Хід уроку
І. Організаційний момент.
Забезпечення емоційної готовності до уроку.
Всі ми разом мов сім`я.
Друзі ми: і ти, і я.
-Добрий день, сусіду зліва.
-Добрий день, сусіду справа.
Ми усі – одна сім`я.
Всі ми разом мов сім`я.
Друзі ми: і ти, і я.
Посміхнись сусіду зліва.
Посміхнись сусіду справа.
Ми усі – одна сім`я.
ІІ. Перевірка домашнього завдання
- Взаємоперевірка.
Перевірка домашнього завдання здійснюється як взаємоперевірка зошитів учнів за зразком, підготовленим заздалегідь на дошці(на слайді).
Слайд 1 Слайд 2
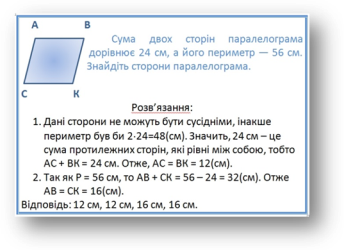
Задача 3.Розв'язання
ІІІ. Актуалізація опорних знань учнів
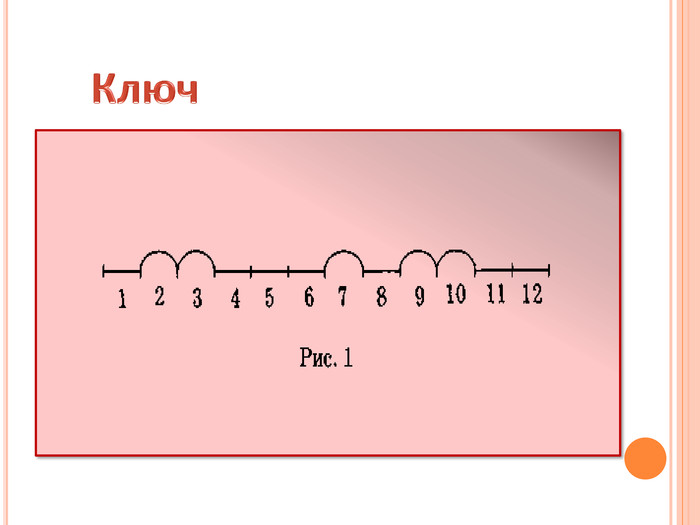
- Вправа «Графічний ланцюжок»
Учитель пропонує учням графічно відповісти на питання(можна на аркушах паперу), позначаючи позитивну відповідь значком 
, негативну — значком 
. Завдання відображаються на слайді – з обов’язковим анімуванням кожного питання. Відповідь матиме вигляд ключа (рис. 1). Після виконання диктанту є обов'язковим його перевірка та обговорення. Ключ відображається теж на слайді – наступному. Аркуші здаються вчителеві до появи ключа на слайді.
Ключ Слайд 3
Слайд 4
ІV. Формулювання мети і задач уроку.Мотивація навчальної діяльності.
Слово вчителя. Ну, ось, ви показали, як добре знаєте всі властивості та ознаки нашої надзвичайної фігури - паралелограма. А сьогодні ми будемо застосовувати їх до розв’язування задач різного рівня складності.
V. Закріплення засвоєних навичок і вмінь учнів
1. Робота в групах. Розв'язання задач.
Учитель пропонує учням вибрати на даний урок задачі доступного рівня й об'єднатися в групи одного рівня. Також організовує роботу груп, які розв'язують задачі достатнього та високого рівнів, створюючи короткотривалі проекти, а з групою учнів, які розв'язують задачі середнього рівня, працює сам.
Група середнього рівня
|
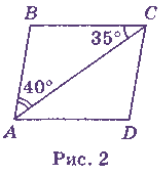
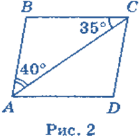
Задача 1. Знайдіть кути паралелограма ABCD (рис. 2).
Оскільки AB || CD і АС — січна, то Відповідь: 75°, 75°, 105°, 105°.
|
|
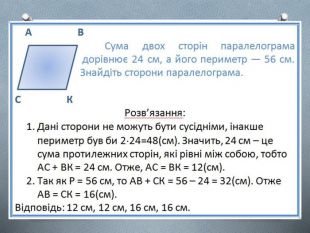
Розв'язання Із умови задачі та властивості діагоналей паралелограма випливає, що йдеться про сусідні вершини паралелограма. Тобто 3 см і б см — це половини діагоналей. Отже, діагоналі дорівнюють 6 см і 10 см. Відповідь: 6 см, 10 см.
|
Група достатнього рівня
|
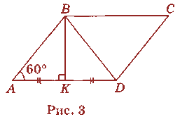
Розв'язання
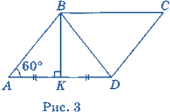
Нехай на рис. 3 АК = KD = x см (х> 0). У прямокутному трикутнику АВК ( Відповідь: 12 см.
|
Група високого рівня
|
Задача 4. Периметр паралелограма дорівнює 90 см, його гострий кут дорівнює 60°. Діагональ паралелограма ділить його тупий кут у відношенні 1:3. Знайдіть сторони паралелограма. Розв'язання
Відповідь: 15 см, 15 см, 30 см, 30 см. |
- Фізкультхвилинка
Щось не хочеться сидіти,
Треба трохи відпочити.
Руки вгору, руки вниз,
Руки в боки, руки так,
Руки вгору, як вітряк.
Вище руки підніміть
І спокійно опустіть.
Плесніть, діти, кілька раз.
За роботу, все гаразд!
- Захист проектів
Після розв’язання учні з груп середнього та достатнього рівнів захищають свої роботи біля дошки. Група високого рівня здає свій проект вчителю на перевірку
VІ. Підбиття підсумків уроку
Методична ремарка
Учитель відзначає роботу найактивніших учнів, які розв'язували задачі середнього рівня, оцінює захист задач достатнього рівня та збирає зошити для перевірки самостійної роботи учнів, які розв'язували задачу високого рівня.
-
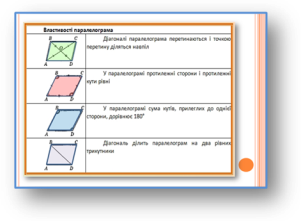Бесіда.
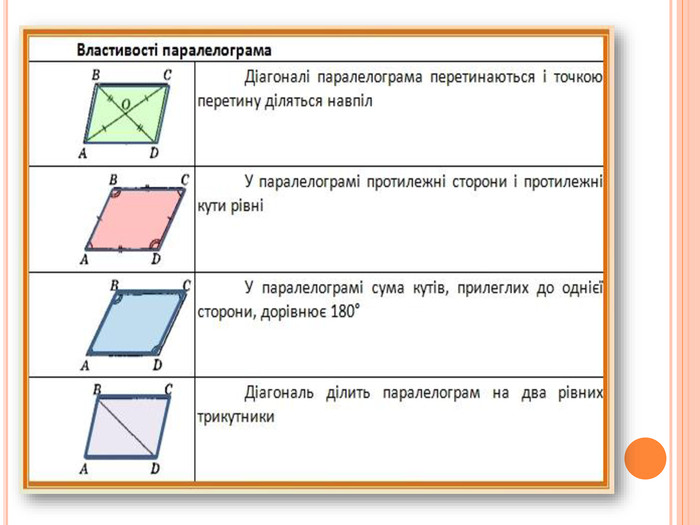
Учні ще раз називають ознаки та властивості паралелограма(за слайдами попереднього уроку). Обов’язково залучити до цього тих учнів, які працювали над задачами середнього рівня.
Слайд 5
VIІ. Домашнє завдання
-
Повторити властивості та ознаки паралелограма.
- Розв’язати задачі:
- Дві сторони паралелограма відносяться як 3:4, його периметр дорівнює 2,8 м. Знайдіть сторони паралелограма.
-
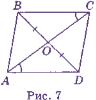
Дано:
OAD = OCB; BO = OD (рис. 7). Довести: ABCD — паралелограм.
про публікацію авторської розробки
Додати розробку