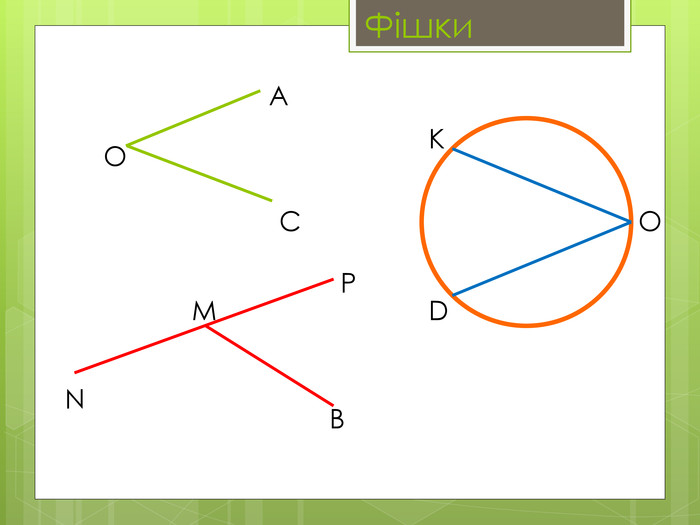
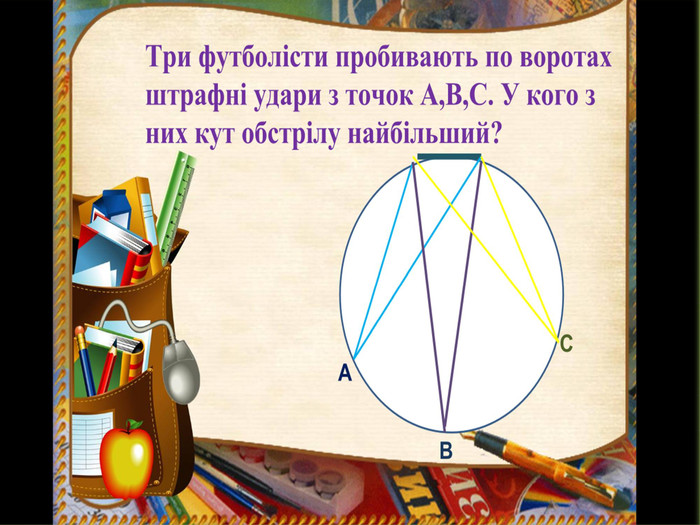
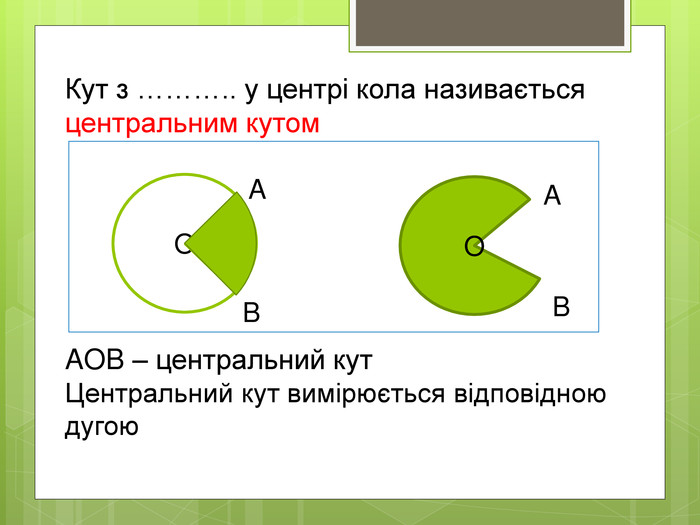
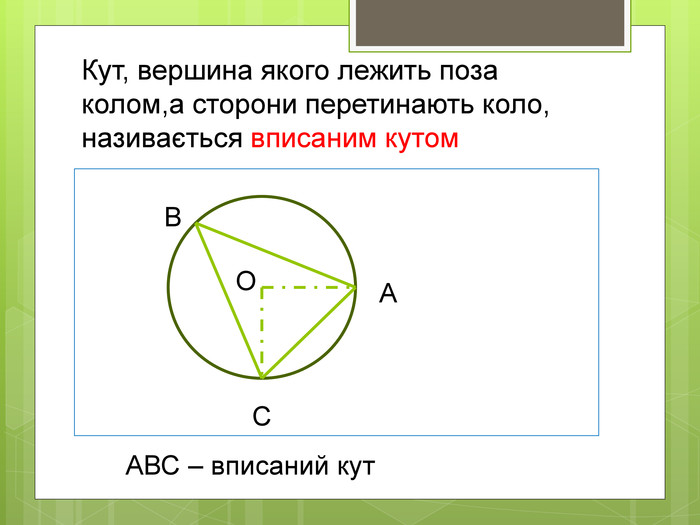
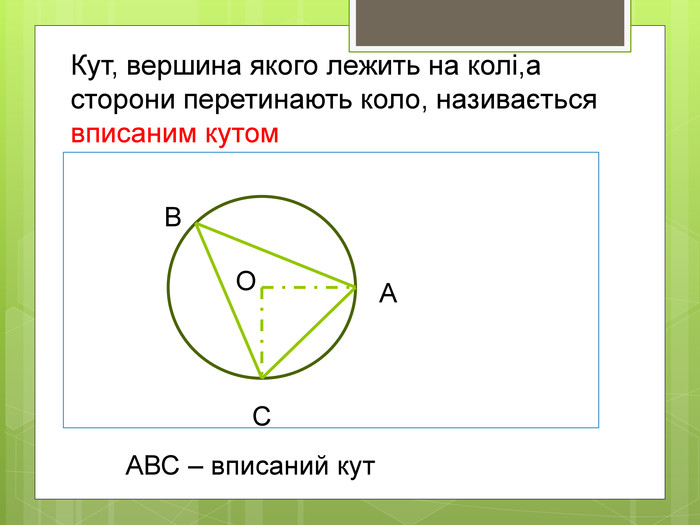
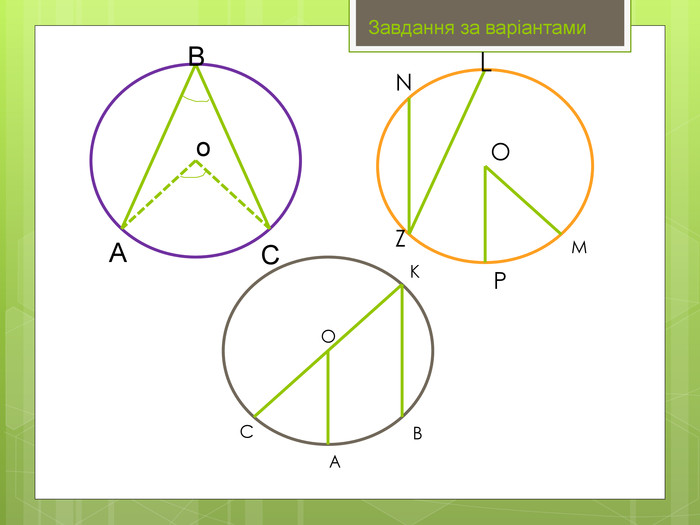
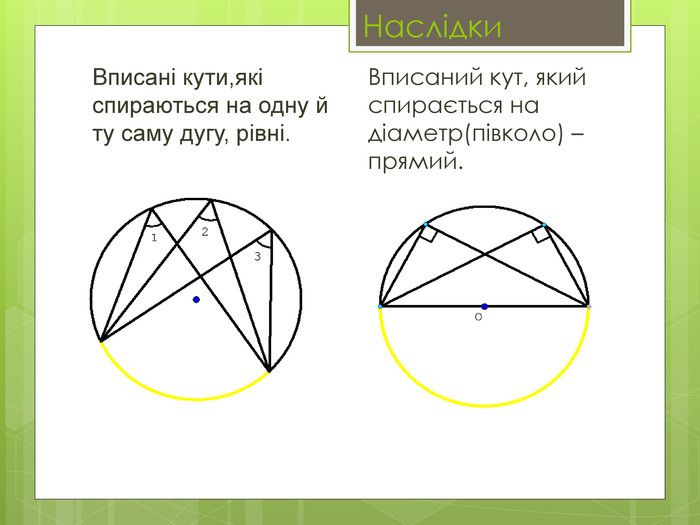
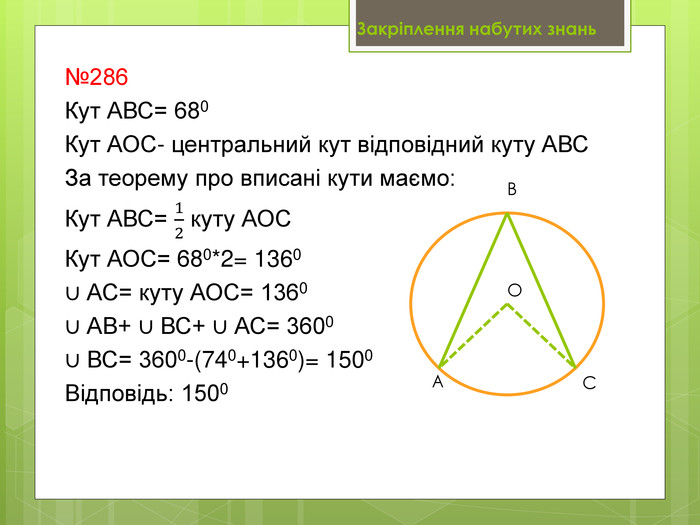
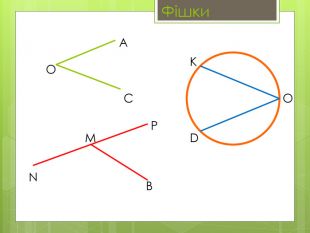
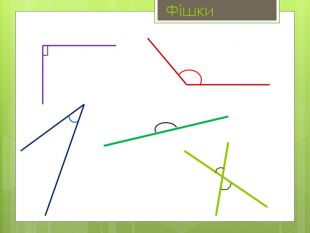
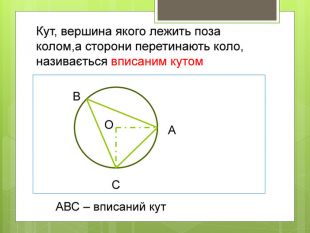
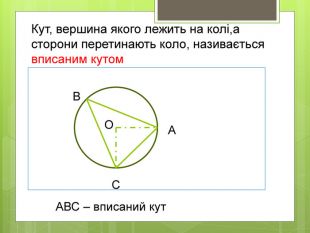
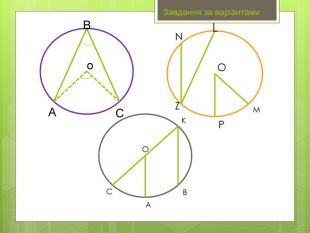
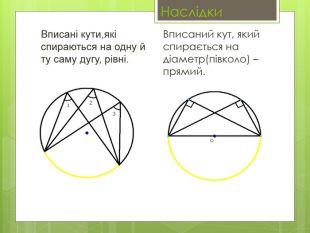
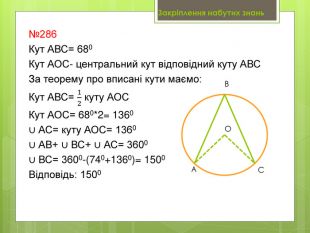
Вписані та центральні кути.
Про матеріал
Мета.
• Навчальна: сформулювати означення вписаного та центрального кутів, ознайомитися з теоремою про вписані кути та наслідками з теореми, навчити учнів застосовувати теорему до розв’язування задач.
• Розвиваюча: розвинути вміння використовувати геометричні поняття під час розв’язування задач, робити висновки, розвинути логічне та абстрактне мислення, пам’ять.
• Виховна: виховувати уважність, свідоме ставлення до навчання, пізнавальний інтерес, охайність.
Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку