Урок геометрії у 8 класі з теми: «Площа трапеції»

Урок геометрії у 8 класі  з теми: «Площа трапеції»

Тема: Площа трапеції

Мета:

 навчальна: вивести формулу площі трапеції, формувати навички і вміння користуватися нею при розв’язуванні задач;

 розвивальна: розвивати у дітей уміння узагальнювати, логічно мислити, застосовувати у своїх думках аналогію, спостережливість, раціонально використовувати свої знання ;

 виховна: виховувати інтерес до предмету, знайомити учнів з історичними фактами, пов’язаними з даною темою.

Тип уроку: комбінований урок.

Обладнання і наочність: конспект уроку, підручник, роздатковий матеріал, комп’ютерна презентація, проектор, набір демонстраційного креслярського приладдя.

Структура уроку:

     І. Організаційний етап. Перевірка готовності учнів до уроку.

ІІ. Перевірка домашнього завдання. Актуалізація і корекція опорних знань.

ІІІ. Повідомлення теми, цілей і завдань уроку, мотивація учіння.

     IV. Сприйняття та первинне усвідомлення нового матеріалу, осмислення     

     зв’язків і відношень в об’єктах вивчення.

     V. Узагальнення і систематизація знань.

     VI. Підведення підсумків, повідомлення домашнього завдання.

Хід уроку

І. Організаційний етап. Перевірка готовності учнів до уроку.

 Вчитель. Всім доброго дня!

 Учні (разом). Доброго дня. Міцного здоров’я!

    Мирного неба кожного дня!

ІІ. Перевірка домашнього завдання. Актуалізація і корекція опорних знань.

 Перевіримо домашнє завдання. Задачу № 734 розв’яже один учень біля дошки, інші працюють усно, даючи відповіді на запитання.

Усне опитування

1. Чому дорівнює площа квадрата? прямокутника? паралелограма? ромба? трикутника? прямокутного трикутника? ( Площа квадрата зі стороною 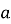дорівнює 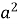. Площа прямокутника дорівнює добутку його сусідніх сторін. Площа паралелограма дорівнює добутку його сторони та висоти, яка проведена до цієї сторони. Площа ромба дорівнює половині добутку його діагоналей. Площа трикутника дорівнює половині добутку його сторони та висоти, яка проведена до неї. Площа прямокутного трикутника дорівнює половині добутку катетів.).
2. Сторони прямокутника дорівнюють 5 см і 3 см. Яка площа прямокутника? ().
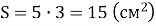3. Сторона квадрата 11 см, яка його площа? ().
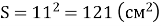4. Площа квадрата 64 см² , яка його сторона? ().
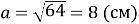5. Діагоналі ромба дорівнюють 10 см і 6 см, чому дорівнює його площа?

().

6. Площа прямокутника 48 см² , одна із його сторін 8 см. Обчисліть його іншу сторону. ().
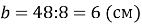7. Катети прямокутного трикутника10 см і 18 см. Знайдіть його площу.

().

Розгорніть свої зошити, перевірте письмову домашню роботу.

№ 734

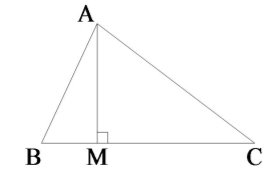           Дано:

       

       см

        см

       

       Знайти: .

Розв’язання

 

 Розглянемо , , оскільки , то – рівнобедрений з основою , .

 

 Розглянемо , , за теоремою Піфагора:

Відповідь. .

ІІІ. Повідомлення теми, цілей і завдань уроку, мотивація учіння.

 Запишіть дату, класна робота у зошити.

 Сьогодні на уроці випала така нагода, бо математика є дивовижною вчителькою у мистецтві спрямувати думки, наводити порядок, викорчовувати безглуздя. Мислити правильно треба всім: і робітникові, і інженерові, і вченому, і художнику, і архітектору, і поету, тому покажемо, як математику застосувати у практичному житті.

Задача. Актова зала школи  має форму трапеції з основами 20 м і 10 м та висотою 8 м. Чи вистачить 9 кг фарби, щоб пофарбувати підлогу актової зали, якщо витрати фарби становлять 1 кг/10 м²?

Слайд 1. Задача

 Що необхідно, щоб розв’язати дану задачу?

 Правильно, потрібно знайти площу трапеції.

Ми вже знаємо, як знаходити площу квадрата, прямокутника, паралелограма, трикутника, ромба.  А зараз виведемо формулу для обчислення ще одного многокутника, а саме трапеції. Тож тема нашого уроку «Площа трапеції»

Слайд 2. Тема уроку. Площа трапеції.

  

Софія Ковалевська сказала: «У математиці є своя мова – це формули».

 Повторимо відомості про трапецію.

Слайд 3. Перевір себе.

• Що називається трапецією?( Трапецією називається чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні).
• Як називаються сторони трапеції? (Паралельні сторони трапеції називаються основами, а непаралельні – бічними сторонами).
• Які види трапецій вам відомі? (Трапеції бувають довільні, рівнобічні та прямокутні).
• Що відомо про кути трапеції, які прилягають до бічної сторони? (Сума двох кутів прилеглих до бічної сторони дорівнює 180⁰).
• Що називають середньою лінією трапеції? (Середньою лінією трапеції називають відрізок, який сполучає середини бічних сторін).
• Чому дорівнює середня лінія трапеції? (Середня лінія трапеції паралельна основам і дорівнює половині їхньої суми).
• Що називають висотою трапеції? (Висотою трапеції називають перпендикуляр, опущений з будь-якої точки прямої, яка містить одну із основ на пряму, що містить другу основу).

При виконанні різного виду робіт (покрити дах будинку, пошити спідницю, пофарбувати стіл) потрібно обчислити площу трапеції.

Слайд 4. Трапеція навколо нас

IV. Сприйняття та первинне усвідомлення нового матеріалу, осмислення зв’язків і відношень в об’єктах вивчення.

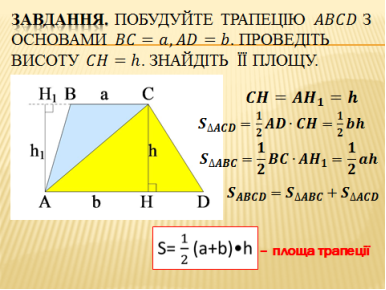
 Слайд 5. Завдання. Побудуйте трапецію з основами                      

. Проведіть висоту . Знайдіть її площу.

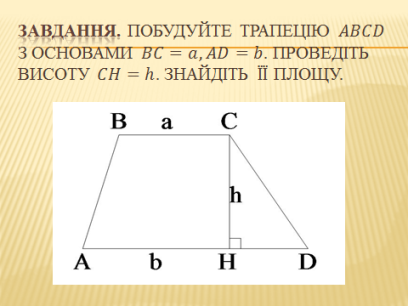
 Проведіть діагональ і висоту . Відрізки і є висотами трикутників і відповідно, в свою чергу дані висоти мають однакову довжину, тому . Вам відомо, як знайти площу трикутника, якщо відомо його сторону та висоту, проведену до неї. Площа трикутника дорівнює половині добутку його сторони  та проведеної до неї висоти.

 ,

.

 Повернімось до трапеції. Трапеція складається з двох даних трикутників. Вам відомо, що якщо многокутник складено з кількох многокутників, то його площа дорівнює сумі площ цих многокутників, тому площа трапеції дорівнює:

 .

 Виділіть одержану формулу рамочкою, підпишіть її назву, вкажіть, що означають букви – основи, - висота.

Слайд 6. Формула площі трапеції

 Розв’язання до задачі:

(м²)

120 : 10 =12 (кг) – фарби потрібно для пофарбування підлоги актової зали

Відповідь. Не вистачить 9 кг фарби для пофарбування підлоги

 Розгорніть підручник на сторінці 160, теорема 23.1 у формулі площі трапеції  – півсума основ.

 Чому дорівнює півсума основ? (Півсума основ дорівнює середній лінії ). Тобто площа трапеції дорівнює добутку її середньої лінії на висоту. Про це свідчить наслідок з теореми на сторінці 161.

Запитання до учнів: 1. Як знайти площу трапеції?

                                      2. Які відрізки потрібно мати для цього?

Практичне завдання. (Обміняйтесь зошитами) Побудуйте довільну трапецію, проведіть висоту. (Знову обміняйтесь зошитами). Виміряйте потрібні відрізки, запишіть їх довжини. Знайдіть площу трапеції.

(Хто впорався № 772 ()

V. Узагальнення і систематизація знань.

№ 774

Дано: - трапеція

       

       см

       

       

       Знайти: .

Розв’язання

 Нехай  тоді

 

 

     

 

 

 

 

 Отже, .

Відповідь. .

 Що ж мабуть прийшла пора трохи відпочити, хочу на фізкультхвилинку вас запросити.

Слайд 7. Фізкультхвилинка.

Всі ми знаєм, щоб списати,

Нам не треба всім моргати.

Підглядаєм вправо, вліво,

Ось уже й задача ціла.

Щоби дать очам спочити,

Треба нам ось так зробити:

Подивитись знизу вгору

Ну, а потім і праворуч.

Знову вниз, ліворуч, так

Є уявний в нас квадрат,

Вправу цю продовжим далі,

Проведем діагоналі.

Оглядаємось навколо,

Намалюємо очима коло

Зажмурімося щосили,

І заплющим очі вмить

Щоби очі відпочили,

Треба ще раз повторить.

 Очі відпочили, продовжуємо працювати.

 А зараз ми з вами спробуємо розв’язати задачі практичного змісту. Задачі отримуємо по рядах, в кожному ряді є учні-консультанти, які допомагатимуть всім іншим виконати завдання та прокоментують його.

 І ряд. Поперечний переріз траншеї має форму трапеції. Обчислити площу цього поперечного перерізу, якщо глибина траншеї 1,5 м, ширина в землі 0,8 м, на поверхні землі 1,2 м.

 ІІ ряд. Для захисту ґрунту від ерозії в районі джерела спроектуйте дамбу, що являє собою трапецію, висотою 3 м і шириною зверху і знизу 2 м і 4 м відповідно. Знайти площу поперечного перерізу  дамби.

 ІІІ ряд. Площа лісу має форму трапеції. Обчисліть скільки дерев загинуло під час лісової пожежі, якщо відомо, що ширина вужчої частини лісу була 3 км, ширшої – 5 км, довжина лісу – 2 км, на 1 км² росло приблизно 200 дерев.

– дерев загинуло під час лісової пожежі

Слайд 8. Задачі практичного змісту

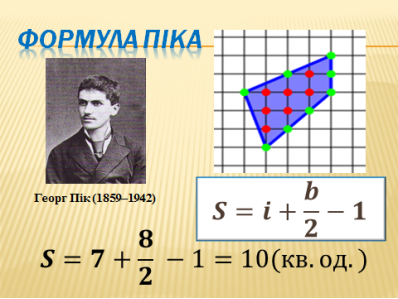
А зараз ми з вами познайомимось із формулою Піка.

Слайд 9. Історична довідка. Формула Піка

Георг Пік – австрійський математик. Народився 10 серпня 1859 року у Відні. Теорема Піка – класичний результат в комбінаторній геометрії і геометрії чисел. Формула Піка була відкрита Георгом Піком в 1899 році. За цією формулою площа многокутника з  цілочисловими вершинами рівна сумі:

,

де –  кількість цілочислових точок усередині многокутника, – кількість цілочислових точок на межі многокутника.

 Точка координатної площини називається цілочисловою, якщо обидві її координати цілі числа. В прикладі на малюнку отже площа рівна

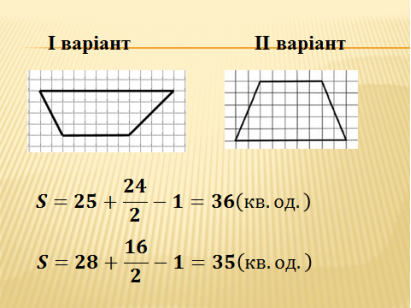
 А зараз ви спробуйте обчислити площу трапеції, використовуючи формулу Піка. Задачі виконуємо по варіантах і колективно коментуємо.

VI. Підведення підсумків, повідомлення домашнього завдання.

Слайд 10. Тестові завдання.

 Ви отримали тестові завдання на листках, підпишіть їх і відповідайте.

1. Чи  є трапеція жорсткою фігурою?

а) так

б) ні

2. У трапецію можна вписати коло, якщо:

а) сума протилежних кутів рівна

б) сума протилежних сторін рівна

в) а) і б)

3. Навколо трапеції можна описати кола, якщо:

а) сума протилежних кутів рівна

б) сума протилежних сторін рівна

в) а) і б)

4. Запишіть формулу для обчислення площі паралелограма.
5. Запишіть формулу для обчислення площі трапеції.
6. Чи може бути діагональ трапеції перпендикулярною до бічної сторони?

а) так

б) ні

7. Площа квадрата дорівнює 100 дм² . Чому дорівнює сторона квадрата?         

     а) 20 дм

     б) 10 дм

     в) 50 дм

8. Площа паралелограма, сторона якого 20 см, а висота, проведена до цієї сторони – 8 см, дорівнює:

     а) 80 см²

        б) 160 см²

9. Площа прямокутника дорівнює 24 см² , довжина – 6 см. Чому дорівнює ширина прямокутника?

     а) 4 см

б) 18 см

в) 12 см

10.  Чому дорівнює площа квадрата, якщо його периметр дорівнює 40 см?

    а)160 см²   

    б)100 см²

Слайд 10 – 11. Тестові завдання

 

Слайд 12. Відповіді на тестові завдання:

1. б) 2. б) 3. а)                       4.                                                 5.

6. а) 7. б)                          8. б) 9. а)                         10. б)

 

Перевірка тестових завдань (взаємоперевірка). Обміняємось із сусідом по парті своїм тестом та здійснимо перевірку тестових завдань. Запишіть кількість правильних відповідей.

Додаткове завдання. Робота з підручником за готовим рисунком.

№ 786

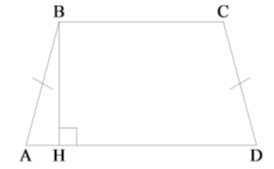
Дано: – трапеція

       см

       

       Знайти: .

Розв’язання

 Проведемо висоту . Розглянемо – прямокутний                 (, – за умовою задачі. За властивістю гострих кутів прямокутного трикутника, . За властивістю катета, що лежить проти кута , маємо

(см)

 За теоремою Піфагора з :

У трапецію можна вписати коло, тому

(см)

 (см²)

Відповідь. см².

 

Слайд 13. Підсумок уроку

• Що я повторив? (-ла?)
• Що я нового вивчив? (-ла?)
• Де я застосую отримані знання?
• Як можна знайти площу трапеції?

 

Ви з кожним днем все більше переконуєтесь, що навколишній світ – це

світ геометрії. А куди в геометрії, без формул. Тож «У математиці є своя мова – це формули.»

Слайд 14. Домашнє завдання

Вивчити: § 23.

Письмово: Початковий і середній рівень: № 775. 778.

                   Достатній і високий рівень: № 783, 789.

Творче завдання: Скласти і розв’язати 2 задачі практичного змісту із використанням формули площі трапеції.

Додаткове завдання (для допитливих):  Опрацювати площу опуклого чотирикутника

Рефлексія

Психологічний тренінг

 В кожного на парті лежать смайлики настрою, підпишіть їх, візьміть олівець, заплющте очі і намалюйте на зворотній стороні смайлика будь-яку геометричну фігуру. Розплющте очі й подивіться на дошку, з якою із трьох запропонованих асоціюється ваша фігура.

 Квадрат – асоціюється з такими рисами характеру, як наполегливість, упертість, твердість характеру.

 Трикутник – наполегливість, упевненість у собі, уміння вислуховувати іншого, прислуховуватися до порад та впевнено йти до поставленої мети.

 Коло – означає емоційність, схильність перейматися проблемами інших як власними, співчувати, виявляти доброзичливість, відвертість.