Урок геометрії з використанням елементів STEM-освіти у 8 класі "Крокуючи за Піфагором"

Урок геометрії з використанням елементів STEM-освіти у 8 класі

                                                           Підготувала:

                                               учитель математики

                                               Берегівського ЗЗСО І-ІІ ст                           

                                                 Новіцька М.І.

Тема.  Теорема Піфагора

Мета: навчальна: систематизувати відомості про прямокутний трикутник; формувати навички знаходження різних способів доведення теореми Піфагора; показати застосування набутих знань в практичній діяльності;

розвивальна: розвивати просторову уяву, вміння аналізувати, робити висновки, працювати творчо;

виховна: виховувати активність, увагу та спостережливість.         

Тип уроку: урок засвоєння нових знань

Обладнання: підручник, косинець, портрет Піфагора, кольорова крейда, кольорові стрічки, геометричні пазли, аркуші для практичної роботи. Мотузка з вузликами

Хід уроку

Гарно прибраний клас. На стіні висить портрет Піфагора, На дошці із кольорових стрічок зроблено прямокутний трикутник, і напис:

«Мов світла промінь в темну пору,

Приходить істина до нас,

Як теорема Піфагора

Вона несхибна повсякчас».

І. Організаційна частина.

   Вступне слово вчителя:

              Прямокутний трикутник – одна з перших геометричних фігур, про властивості якої людство дізналось ще в давнину. Задачі про  трикутник знаходять у давньоєгипетських папірусах, старовинних індійських книгах. У папірусі Ахмеса згадується про властивості рівнобедреного та прямокутного трикутників, давні вавілоняни 4000 років тому вже знали про кути при основі рівнобедреного трикутника. Ознаки рівності трикутника були сформовані Евдемом Родоським та Фалесом Мілетським. У Давній Греції в іонійській математичній школі (заснована а VI столітті до нашої ери Фалесом) та у школі Піфагора знали види й властивості трикутників. Систематизував ці відомості Евклід у першому трактаті з геометрії «Началах».

             Чому ж трикутник цікавив людей з давніх часів? Жорсткість трикутників використовували під час будівництва й конструювання.

ІІ. Актуалізація опорних знань учнів.

     Евристична бесіда з класом (за технологією «Мікрофон»): Учень дає відповідь на одне запитання та передає мікрофон наступному учневі.

1. Що таке трикутник?
2. Які є види трикутників?
3. Який трикутник називається прямокутним?
4. Як називаються сторони прямокутного трикутника?
5. Намалюйте на дошці рівнобедрений прямокутний трикутник і назвіть усі його сторони та градусні міри кутів цього трикутника.

ІІІ. Мотивація навчальної діяльності.

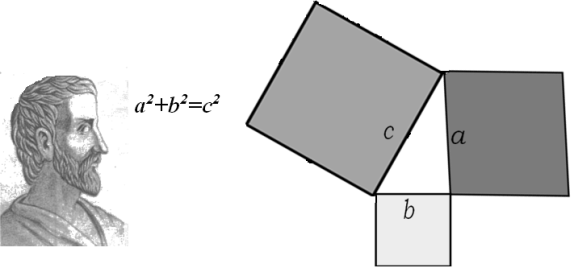
   Найпопулярнішою з усіх теорем планіметрії є теорема Піфагора. Причинами такої популярності є простота, краса і значення.

   Про теорему Піфагора так сказав німецький вчений Йоганн Кеплер: «У геометрії є два скарби: перший – теорема Піфагора, другий – золотий поділ. Перший можна порівняти з мірою золота, другий – із коштовним каменем».  

   Цю теорему називають вічною. Їй понад 2 тисячі років. В епоху Середньовіччя її називали «ослячим містком», тому що довести її було важко для тогочасних науковців. Тож спробуємо і ми перейти цей «ослячий місток».

У 1974 році до сузір’я Геркулес було відправлено потужний радіосигнал, який містив у собі 1679 різних повідомлень про людство, його наукові та культурні надбання, планету Земля, її хімічний склад та розміри. Серед них була   зашифрована і теорема Піфагора.       Дізнатись про те, чи змогли інші істоти у всесвіті розшифрувати і зрозуміти цю теорему ми зможемо дізнатися лише через 5 тис років (саме через цей проміжок часу повернеться сигнал назад на Землю). А чи зможете зрозуміти її ви, ми дізнаємося вже наприкінці уроку.

ІV.Формування мети й завдань уроку.

        Теорема Піфагора – одна з основних у евклідовій геометрії. Завдяки їй       можна довести та розв’язати не одну задачу. Тому її потрібно добре засвоїти. Сьогодні у нас урок однієї теореми, на якому ми закріпимо знання про теорему Піфагора, розв’яжемо задачі практичного змісту на використання цієї теореми.

А епіграфом нашого уроку пропоную взяти наступні слова великого Піфагора:  «Добре засвоєна мудрість не забувається      ніколи»       Піфагор.                                                                                                                                                                                                    

V. Перевірка домашнього завдання.(Усний журнал)

Ви вдома готували усний журнал про математика, іменем якого названа ця теорема.

1 учень. 

    Легенда про народження

         Піфагор жив у 6 столітті до нашої ери. Він  народився у Греції, на острові Самос у сім’ї  золотих справ майстра Мнесарха.  За легендою оракул пророчив йому та його дружині Парфенісі народження сина, який буде славитися віками своєю мудрістю,  справами та красою. Пророцтво збулося, і тоді Парфеніса приймає ім’я Піфіада, на  честь Аполлона Піфійського, а сина називає Піфагором, на честь пророцтва Піфії. У легенді нічого не сказано про рік народження Піфагора, історичні дослідження датують його появу на світ приблизно 580 роком до нашої ери.

   Дитячі та юнацькі роки

            Можливості дати сину гарну освіту та виховання у Мнесарха були. Як і будь-який батько, Мнесарх мріяв, що син буде продовжувати його справу – ремесло золотих справ майстра. Життя вирішило інакше. Майбутній математик та філософ вже в дитинстві виявив велику здатність до наук. У свого першого вчителя Гермодамаса Піфагор отримав знання основ музики та живопису. Для покращення пам’яті Гермодамас примушував його вчити пісні з «Іліади» та «Одіссеї». Перший вчитель навчив Піфагора любити природу та вивчати її таємниці.

           Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання в Єгипті, у жерців. Потрапити до Єгипту у той час було дуже важко, тому що країну практично закрили для греків. За допомогою вчителя Піфагору вдається залишити острів Самос. Але до Єгипту далеко, і Піфагор поки що живе на острові Лесбос. Там відбувається знайомство Піфагора з філософом Ферекідом – другом Фалеса. У Ферекіда Піфагор навчається астрології, таємницям чисел, медицині та іншим обов’язковим, на той час, наукам. Піфагор прожив на Лесбосі кілька років. Звідти шлях Піфагора лежить у Мілет до відомого Фалеса, засновника першої в історії філософської школи.

             Навчання Піфагора в Єгипті сприяє тому, що він стає одним із найбільш освічених людей свого часу. Волею долі 12 років прожив Піфагор у Вавилоні, де прилучився до східної астрології та містики. І тільки в 60 років Піфагору вдалося повернутися на Батьківщину.

Піфагорійська школа

           Після повернення додому Піфагор переселився  до Південної Італії, яку  тоді називали великою  Грецією. Тут, на острові  Сицилія в Кротоні, у нього  народжується власна  філософська школа.

          Це був одночасно і релігійний союз, і політичний клуб, і наукове товариство. Учні цієї школи зобов’язувались вести так званий піфагорійський спосіб життя. Статут піфагорійського союзу був дуже суворим. Кожний, хто вступав до нього, відмовлявся від особистої власності на користь союзу, зобов’язувався не проливати крові, не вживати м’ясної їжі, берегти таємницю вчення свого вчителя. Членам школи заборонялося навчати інших за винагороду. Всі учні Піфагора і він сам були працелюбні. Досконало володіючи методами єгипетських жерців, Піфагор «очищував душі своїх слухачів, виганяв вади з серця та наповнював уми світлою правдою». В «Золотих віршах» Піфагор показав ті моральні правила, суворе виконання яких призводить до ідеалу. Ось декілька з них:

        1) Роби лише те, що в результаті не засмутить тебе і не примусить каятися.

 2) Не роби ніколи того, чого ти не знаєш. Але навчися усього, що варто знати, і тоді будеш вести спокійне життя.

 3) Не зневажай здоров’ям свого тіла. Доставляй йому вчасно їжу і питво, і вправи, без яких воно бідує.

 4) Привчайся жити просто, без розкоші.

 5) Не закривай очей, коли хочеться спати, не проаналізувавши успіх своїх вчинків за минулий день.

 6) Не порушуй справедливість.

 7) Не сідай на подушку (тобто не зупиняйся на досягнутому).

 8) Не гризи свого серця (тобто не піддавайся меланхолії).

 9) Не поправляй вогню мечем (тобто не дратуй тих, хто і без того в гніві).

 10) Не приймай під свій дах балакунів і легковажних людей.

          На персні Піфагора було викарбувано

 такий девіз: «Тимчасова невдача краща

 тимчасової удачі».

         У якості символа піфагорійці вибрали пентаграму – п’ятикутну зірку. Це символ здоров’я і досконалості, опізнавальний знак піфагорійців.

Піфагорійцями було зроблено багато важливих відкриттів в арифметиці і геометрії, в тому числі: теорема про суму внутрішніх кутів трикутника; побудова правильних багатокутників і ділення площині на деякі з них; геометричні способи розв'язання квадратних рівнянь; розподіл чисел на парні і непарні, прості і складені; створена математична теорія музики

VІ. Вивчення нового матеріалу.

а) Дослідницька робота в групах.

А зараз спробуємо скласти пазл. У вас на столах лежать три квадратика та трикутник. Ваша задача з’єднати сторони, що мають однакову довжину. Зараз виміряйте сторони квадратів і знайдіть їх площі. Наступне завдання: додайте площі малих квадратів та порівняйте з площею великого квадрата.

Висновок: Сума площ квадратів, побудованих на катетах, дорівнює площі квадрата, побудованого на гіпотенузі.

Вітаю – ви тільки що практично довели теорему Піфагора.

б) Практична робота в групах:

    У вас на столах лежать аркуші для практичної роботи. Поділіться на пари. Виміряйте у см сторони своїх трикутників і позначте катети а =  ,b = , с =  . Тепер піднесіть усі виміри до квадрату. Додайте квадрати катетів і суму порівняйте з квадратом гіпотенузи.

Висновок: Квадрат гіпотенузи дорівнює сумі квадратів катетів (це сучасне формулювання теореми Піфагора). Запишіть формулювання.

в) Доведення теореми Піфагора.

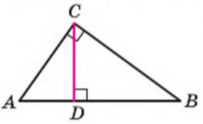Дано: ∆АВС, С=90º.

Довести: AB²=АС² + BC²

Доведення

Проведемо висоту CD. Застосувавши теорему про метричні співвідношення для катетів АС і ВС, отримаємо:

АС² = AB  АD

BC²= AB  DВ

 АС² + BC² = AB  АD + AB  DВ= AB (АD + DВ) = AB  AB = AB²

Якщо в прямокутному трикутнику довжини катетів дорівнюють a і b, а довжина гіпотенузи с, то т.Піфагора можна виразити такою рівністю

г) Наочне доведення теореми Піфагора.

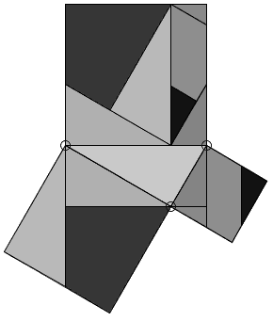д) Дослідницька робота. І ще одне цікаве завдання: ви бачите перед собою мотузку з вузликами. Спробуйте з цієї мотузки скласти трикутник із сторонами 3 частини, 4 частини, 5 частин. А тепер виміряйте кут, що утворили сторони з вимірами 3 та 4 частини. (90 ̊ ).

Кажуть, що саме так єгипетські будівельники відкладали прямі кути і побудували великі Єгипетські піраміди. (формулюємо означення єгипетського трикутника)

VІІ. Закріплення знань. Формування навичок.

а)Задачі за готовими рисунками.

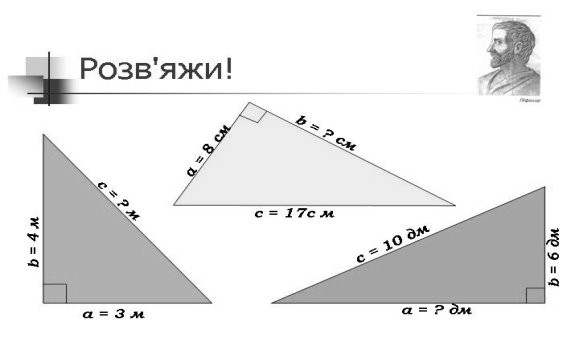
б) розв’язування задач практичного характеру )

Задача  І

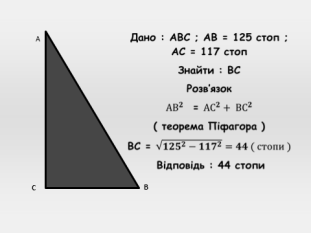
Старовинна задача

    Сталося якомусь чоловіку до стіни драбину поставити , стіни ж тої висота є 117 стоп .І відати хоче він , на скільки стоп драбини нижній кінець від стіни отстояти має , якщо драбини довжина 125 стоп .

Задача  ІІ

Дах будинку має форму рівнобедреного трикутника ( АВС) , АВ=50м ,основа трикутника АС = 96м . Знайти висоту даху

Задача ІІІ

     Висота новорічної ялинки 8 м. Для закріплення її у вертикальному положенні від вершини ялинки зробили натяжки АВ, АВ₁, АВ₂ однакової довжини і закріпили їх на підлозі на відстані 6 м від основи ялинки. Якої довжини повинна бути натягуюча проволока, щоб ялинка стояла вертикально.

VІІІ. Теорема Піфагора в літературі.

Теорема Піфагора є однією з основних у геометрії. За її допомогою можна вивести більшість теорем геометрії й розв’язувати безліч задач. Цій теоремі навіть присвячені  вірші. (Учень читає вірш )

                                          Про теорему Піфагора

Суть істини проста: вона – дороговказ,

                                      Що сяє для людей, одвічна і сувора,

                                      Тому, як в давнину, вражає нині нас

                                      Беззаперечна теорема Піфагора.

                                      За дотик мудрості уславлених богів,

                                      Ковток із джерела незвіданого смаку,

                                      Олімпу Піфагор тоді осанну звів

   І сто биків заклав жертовних на подяку.

Відтоді всі бики, що чують серед нив,

      Що людство прагне знов за обрії духовні,

Збентеженно ревуть, хоча і ясла повні,

  Такий в них Піфагор навіки жах вселив.

Не зборе бик того, що істина зборола,

   Тому вони й ревуть, схиливши очі долу. 

ІХ. Рефлексія.

Метод «Квітка засвоєння».

Учні прикріплюють на дошці пелюстки квітки:

Зелені – все зрозуміло,

Сині – майже все зрозуміло,

Жовті – зрозуміло наполовину,

Червоні – нічого не зрозуміло.                                                                          

Х. Постановка домашнього завдання.

До наступного уроку ви повинні вивчити теорему Піфагора, бо ми будемо вчитися застосовувати її до розв’язування складніших задач.

Опрацювати п.

Розв’язати задачі:

ІV рівень - Скласти задачі практичного змісту, для розв’язання яких необхідно використати теорему Піфагора. 

ХІ. Підведення підсумків уроку.

Яке відкриття ми сьогодні зробили? Хто зможе нагадати, як формулюється теорема Піфагора? Яку практичну користь дає нам теорема Піфагора?

Отже, сьогодні ви познайомилися з найвідомішою теоремою планіметрії – теоремою Піфагора. Тому люди пам'ятають Піфагора дві з половиною тисячі років.

Діти, попереду у вас ще багато різних теорем життєвих та геометричних.Можливо, з часом теорема Піфагора буде здаватися вам дуже простою. Але сьогодні ви подолали певний рубіж, ви стали розумнішими на цілу теорему – теорему Піфагора, – цікаву, могутню, вічну. Дякую всім за урок!