Урок-інтелектуальна гра

Урок-інтелектуальна гра

 «Засідання клубу знавців математики:

 «Що? Де? Коли?»

Г.В.Філюнкіна

 

ВСТУП

Головною метою завдань загальної середньої освіти є всебічний розвиток дитини, збагачення її цілісної особистості, розвиток здібностей  і обдарувань, формування громадянина України, здатного до свідомого вибору. Тому перед школою, учителем постає дуже важливе завдання – виховувати дитину не тільки здоровою й сильною людиною, а й людиною, яка мислить творчо. У зв’язку з цим підвищується роль учителя математики в підготовці й проведенні уроків. Сучасний учитель повинен створити для дитини таке середовище й таку систему взаємин, які б стимулювали найрізноманітнішу діяльність дитини, поступово розвивали б у неї саме те, що в конкретний момент може найефективніше розвиватися.

Працюючи в школі, прийшла до висновку, що одним із способів розвинути здібності учня, уникнути одноманітності в навчанні допомагають уроки різні за формою проведення: уроки-турніри, уроки-подорожі, уроки змагання. Досить тривалий час  під час узагальнення й систематизації знань і вмінь запроваджую в практику роботи уроки-інтелектуальні ігри. Серед них особливе місце посідають засідання клубу знавців математики «Що? Де? Коли?». 

Такі уроки допомагають

• пробудити й розвинути стійкий інтерес учнів до математики;
• розширити й поглибити знання учнів з програмового матеріалу;
• оптимально розвинути математичні здібності в учнів і прищепити певні навички науково-дослідницького характеру;
• розвинути в учнів уміння самостійно й творчо працювати з навчальною та науково-популярною літературою;
• розширити й поглибити уявлення учнів про практичне значення математики в техніці й практиці, про культурно-історичну цінність математики, про ведучу роль математичної школи у світовій науці;
• виховувати культуру математичного мислення;
• виховувати в учнів почуття колективізму й уміння поєднувати індивідуальну роботу з колективною;
• встановити більш тісні ділові контакти між учителем математики й учнями і на цій основі більш глибоко вивчати пізнавальні інтереси та запити учнів;
• створити учнівський актив, здатний надати вчителю математики допомогу в організації ефективного навчання математики всього колективу конкретного класу (допомога у виготовленні наочних посібників, у пропаганді математичних знань серед інших учнів, залученні до роботи учнів, що мають невисокий рівень навчальних досягнень).

Уроки-засідання клубу знавців математики «Що? Де? Коли?» має таку структуру: 

І. Організаційний момент.

ІІ. Мотивація навчальної діяльності учнів.

ІІІ. Оголошення теми й мети уроку, постановка навчальних завдань.

ІV. Актуалізація опорних знань учнів:

1. Привітання (презентація команд).
2. Розминка (перевірка теоретичних знань).

V. Узагальнення та систематизація знань.

1. Інформаційний конкурс

2. Конкурс капітанів

3. Розв’язування задач

VІ. Підсумки уроку, оцінювання навчальних досягнень учнів.

VІІ. Домашнє завдання та інструктаж щодо його виконання.

За тиждень до уроку обговорюються умови його проведення: детально пояснюються обов’язки кожного члена групи, капітана, обговорюються правила проведення кожного етапу, доводяться до відома критерії оцінювання. Учні класу об’єднуються в команди (кількість команд залежить від кількості учнів у класі). Учитель  пропонує школярам придумати назву команди, її емблему, скласти девіз, який би відображав тему уроку, виконати домашнє завдання, знайти додаткову інформацію за темою. Кожна команда обирає капітана (на перших уроках це може зробити й учитель).

При проведенні розминки бажано, щоб учні мали змогу не тільки чути питання, але й бачити умову (у вигляді презентації або на картках). На роздуми дається 3 секунд, за цей час капітан команди повинен визначитися, який учень відповідає. Після кожної відповіді учитель коментує  відповідь.

При підготовці інформаційного конкурсу  учням пропонується дібрати якомога більше інформації з теми. Знайдена інформація оголошується представниками команди почергово. Перемогу в цьому конкурсі здобуває та команда, яка встигне назвати більше інформації за відведений час.

Для проведення конкурсу «Розв’язування задач» необхідно передбачити наочність завдання (картки або умови у презентації), аркуші для розв’язування, необхідні інструменти. Завдання потрібно добирати, ураховуючи рівень підготовки учнів класу.

На таких уроках доцільно залучати капітанів команд до оцінювання роботи кожного члена своєї команди. Перед початком гри роздати таблицю, у яку капітан вписує кількість балів, яку отримує кожен член своєї команди за підготовку та участь на кожному етапі, а саме:

• за підготовку привітання від 0 до 3 балів, враховується участь у підготовці емблеми, девіза, назви команди;
• за підготовку   інформаційного конкурсу від 0 до 3 балів, враховується кількість інформації з теми, яку підготував учень;
• за підготовку домашнього завдання від 0 до 3 балів, враховується вклад кожного учня при виконанні роботи.

Всі отримані бали додаються до оцінювання відповідей учнів на уроці.

Членам журі при оцінюванні конкурсів потрібно враховувати оригінальність, естетичність, наочність, відповідність інформації до теми уроку, звертати увагу на оформлення презентації та вміння представляти цю інформацію.

Такі уроки подобаються учням. Вони підвищують інтерес до предмета, з’являється бажання працювати творчо. Думаю, що розробки таких уроків або їх елементи можуть бути використані в педагогічній практиці.

 

 

8 клас. Геометрія

Тема. Теорема Піфагора.

Розв’язування прямокутних трикутників.

Мета уроку:

• повторити теорему Піфагора, значення тригонометричних функцій гострих кутів трикутника, вміння розв’язувати прямокутні трикутники, підготувати учнів до контрольної роботи;
• розвивати компетентність учнів з даної теми, уміння знаходити додатковий матеріал з теми, цікавість до геометрії;
• виховувати колективізм, почуття взаємодопомоги при розв’язуванні задач, розвивати естетичні смаки.

Тип уроку: узагальнення й систематизація знань і вмінь.

Обладнання: комп’ютер, проектор, екран, емблеми команд, картки із завданнями для команд,  годинник, сова, на дошці оформлена таблиця, до якої заносяться результати змагань.

 

Хід уроку

І. Організаційний момент

ІІ. Мотивація навчальної діяльності школярів

Слово вчителя.

Як ви вважаєте, чи має математика відношення до музики?

Ні? Даремно ви так вважаєте. Ще давньогрецький математик Піфагор відносив до математики арифметику, геометрію, астрономію та … музику. Саме Піфагор увів поняття гамма, яке  охрестили – Піфагорів устрій.

 

ІІІ. Оголошення теми й мети уроку, постановка навчальних завдань.

Привітання команд з початком гри.

 

На уроці присутнє журі, дозвольте вам його представити.

Учитель оголошує склад журі. До складу журі запрошуються учні класу – переможці олімпіад, учасники Всеукраїнського конкурсу-захисту науково-дослідницьких робіт учнів-членів МАН, учитель математики. Один учень – «хранитель часу», відповідає за дотриманням командами часу на роздуми, відповіді.

 

ІV.  Актуалізація опорних знань учнів

 

1. Привітання

«Найвище призначення математики – знаходити порядок у хаосі, який нас оточує». Норберт Віннер (американський вчений)

Групи учнів презентують команди: назва команди, девіз, емблема.

• Числа Фібоначчі

«По силам будь-які задачі,

Команді «Числа Фібоначчі»

• Знавці

«Не вмієш – навчимо,

Не хочеш – примусимо!»

• Рівняння

«У навчанні першим будь.

Про рівняння не забудь»

Оцінювання від 0 до 12 балів. Критерії: оригінальність 0-3 балів, змістовність 0-3 балів, акуратність 0-3 балів, відповідність теми 0-3 балів.

2. Розминка. 

«Усе впорядковується відносно чисел» Піфагор Самоський (близько 580-500 рр. до н.е.)

 

Питання для 1 команди

1. Дайте означення синуса гострого кута прямокутного трикутника.
2. Знайти значення виразу cos 45⁰· tg 60⁰; sin 60⁰· tg 45⁰.
3. Як знайти катет, якщо відомий другий катет та протилежний кут трикутника?
4. Як змінюється синус гострого кута із збільшенням градусної міри кута?
5. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 12 см і 15 см. Знайдіть другий катет.
6. Якщо радіус описаного кола навколо прямокутного трикутника дорівнює 10 см, то чому дорівнює гіпотенуза?
7. Чи існує прямокутний трикутник, сторонами якого є відрізки довжиною 1 см, 8 см і 6 см?
8. Проекції катетів на гіпотенузу дорівнюють 4 см і 9 см. Знайти довжину висоти, проведеної з вершини прямого кута?
9. Знайти радіус вписаного кола в прямокутний трикутник, якщо його сторони дорівнюють 6 см, 8 см і 10 см.

 

Питання для 2 команди

 

1. Дайте означення косинуса гострого кута прямокутного трикутника.
2.  Знайти значення виразу sin 60^0. tg 30⁰, sin 30^0. tg 45⁰?
3. Як знайти  катет, якщо відома гіпотенуза і протилежний кут?
4. Як змінюється косинус гострого кута  із збільшенням градусної міри кута?
5.  Катет і гіпотенуза прямокутного трикутника відповідно рівні 15см і 17см. Знайти другий катет.
6. Гіпотенуза  дорівнює 30 см, то чому дорівнює радіус описаного кола навколо прямокутного трикутника?
7. Чи існує прямокутний трикутник, сторонами якого є відрізки довжиною 2 см, 7 см і 6 см?
8. Проекції катетів на гіпотенузу дорівнюють 16 см і 9 см. Знайти довжину висоти, проведеної з вершини прямого кута?
9. Знайти радіус вписаного кола в прямокутний трикутник, якщо його сторони дорівнюють 9 см, 12 см і 15 см.

 

Відповіді та коментар для журі:

	2	4	5	6	7	8	9
1 команда	;	збільшується	9 см	20 см	ні	6 см	2 см
2 команда	0,5; 0,5	зменшується	8 см	15 см	ні	12 см	3 см

 

Оцінювання від 0 до 9 балів. Критерії - за кожну правильну відповідь 1 бал.

 

V. Повторення та узагальнення знань

 

1. Інформаційний конкурс

Інформаційний конкурс (кожна команда отримає 1 хвилину, за цей час потрібно навести якомога більше інформації з теми). Відповідають учні команди по черзі.

Приклади інформації з теми:

• медіана, проведена з вершини прямого кута, дорівнює половині гіпотенузи;
• трикутник сторони якого пропорційні числам 3, 4, 5 називається єгипетським;
• катет прямокутного трикутника дорівнює добутку гіпотенузи і синуса протилежного кута;
• радіус кола вписаного в прямокутний трикутник дорівнює …

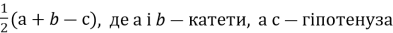Оцінювання від 0 до 12 балів. Критерії: за кожну інформацію, яка відноситься до теми та її правильність – 1 бал.

 

2. Конкурс капітанів  

Капітанам учитель роздає по дві таблички з написами: «ТАК», «НІ». Якщо учень вірить події, яку оголошує вчитель, то піднімає табличку з написом «ТАК», якщо не вірить, то - «НІ».

 

    № 1. Чи погоджуєтеся, що Шарль Перо, автор «Червоного капелюха»,  написав казку «Кохання циркуля та лінійки»?

 Коментар вчителя: Так, є така казка.

 

     № 2. Чи погоджуєтеся, що будь-який трикутник є єгипетським?

Коментар вчителя: Ні, тільки якщо його сторони пропорційні числам 3, 4, 5.

 

№ 3. Чи погоджуєтеся, що Піфагор брав участь у кулачному бою на 58 Олімпіаді, яка проходила у 548 році до н.е.?

Коментар вчителя: Так. Він був чемпіоном з цього виду спорту та утримував це титул  ще на декількох олімпіадах.

 

    № 4. Чи погоджуєтеся, що є книга, яка містить 370 різних способів доведення теореми Піфагора?

Коментар вчителя: Так.  Ця книга була видана у 1940 р.

 

№ 5. Чи погоджуєтеся, що теорему Фалеса називали «ослячий міст»?

 Коментар вчителя: Ні. Так називали теорему Піфагора

 

№ 6. Чи погоджуєтеся, що відомий Фалес був уболівальником і помер на трибуні Олімпійського стадіону в той час, коли був бій Піфагора? (на 58 Олімпіаді)

Коментар вчителя: Так.  Про це є свідчення у літопису.

 

№ 7. Чи погоджуєтеся, що в основі всіх сучасних підручників з геометрії лежать відомі «Начала» Євкліда, які написані у III ст. до н.е.?

 Коментар вчителя: Так. 

 

№ 8. Чи погоджуєтеся, що великий Євклід сказав царю Птолемею: «У геометрії немає царських доріг!»

Коментар вчителя: Так. Євклід жив у 300 р. до н.е.

 

Оцінювання від 0 до 8 балів. Критерії: кожне питання 1 бал за правильність відповіді.

3. Розв’язування задач.

«Жодна людина ще не навчилася думати, читаючи в готовому вигляді записані думки іншої людини. Навчитися думати можна, лише розмірковуючи самостійно» Михай Ємінеску (румунський поет)

 

Задачі для 1 команди

1. У прямокутному трикутнику провели бісектрису гострого кута, яка ділить катет на відрізки 4 і 7 см. На малюнку відмітити довжини отриманих відрізків. Відповідь обґрунтувати.
2. Гіпотенуза прямокутного трикутника на 2 м. більша за один з катетів, а другий катет дорівнює 6 м. Знайти периметр трикутника.

Відповідь: 24 м.

3. Робота з таблицями Брадіса

За допомогою таблиць розв’язати прямокутний трикутник:

Дано ∆АВС, С=90⁰, АВ=20 см, А=41⁰12^/.

Розв’язати прямокутний трикутник.

 

Задачі для 2 команди

1. У прямокутному трикутнику провели бісектрису гострого кута, яка       ділить катет на відрізки 6 і 4 см. На малюнку відмітити довжини отриманих відрізків. Відповідь обґрунтувати.
2. Гіпотенуза прямокутного трикутника на 8 м. більша за один з катетів, а другий катет дорівнює 16 м. Знайти периметр трикутника.

Відповідь: 48 м

      3. Робота з таблицями Брадіса

За допомогою таблиць розв’язати прямокутний трикутник:

Дано ∆АВС, С=90⁰, АВ=10 см, А=41⁰12^/.

Розв’язати прямокутний трикутник.

 

Оцінювання від 0 до 12 балів. Коментар для журі: кожне завдання оцінюється від 0 до 4 балів.

1 завдання:

1 бал - малюнок прямокутного трикутника,

1 бал - побудова бісектриси гострого кута,

1 бал - правильно відмітили відрізки від вершини прямого кута довжина меншого відрізка,

1бал – записати властивість бісектриси кута трикутника.

2 завдання:

1 бал – введення змінної,

1 бал – скласти рівняння,

1 бал – знаходження всіх сторін трикутника,

1 бал – периметр трикутника.

3 завдання:

1 бал – знайдена градусна міра кута,

1 бал – за допомогою таблиць Брадіса знайдено значення синуса або косинуса кута,

1бал – знайдено ВС,

1 бал – знайдено АС.

4. Домашнє завдання.

«Серед рівних розумом, при однакових рівних умовах, перевищує той, хто знає геометрію» Блез Паскаль (французький математик, фізик, філософ)

 

Учням пропонується довести теорему Піфагора, використовуючи доведення інше, ніж у підручнику.

 

Оцінювання від 0 до 12 балів. Критерії: 4  бали - оригінальність, 4 бали - науковість, 4 бали – оформлення.

 

VI. Підсумки уроку, оцінювання навчальних досягнень учнів

Оголошення журі результатів змагань.

 

Слово вчителя:

«У величезному саду геометрії кожен може дібрати собі букет за смаком»  Давид Гільберт

 

Нагородження переможців.

 

Закінчено урок, і виконано план.

Дякую, учні, щиро всім вам.

Бажаємо всім успіхів нехай вам щастить!

Всім дякуємо за урок!

 

VІI. Домашнє завдання та інструктаж щодо його проведення

Розв’язати задачі:

1. З точки А до кола  з центром в точці О проведена дотична АВ. Відомо, що ОВ=9 см, ОА-АВ= 3 см. Знайти відстань від точки А до центра кола і довжину дотичної.

2. Периметр рівнобедреного трикутника дорівнює 96 см. Бічна сторона відноситься до висоти, проведеної до основи, як 5:4. Знайти основу трикутника.

3. Катет прямокутного трикутника дорівнює 8 см, а медіана проведена до нього, см. Знайти периметр трикутника та його гострі кути з точністю до 1⁰.

Заключне слово вчителя:

Існує єдина формула щастя - чесно працювати, поважати один одного та жити у злагоді та мирі.

 

 

 

 

 

Література

 

1. Алгебра: підруч. для 8 кл. загальноосвіт. навч. закл./ О.С. Істер. -  К.: Освіта, 2008.   – 208 с.
2.  Геометрія: підруч. для 8 кл. загальноосвіт. навч. закл./ М.І. Бурда, Н.А. Тарасенкова.  - К.: Зодіак - ЕКО, 2008.   – 240 с.
3. Істер О.С. Тематичні контрольні роботи та завдання для корекції знань з алгебри і геометрії для 8-го класу/- Кам’янець-Подільський, «Абетка», 2002. – 72 с.
4. А.Г. Мерзляк, В.Б. Полонський, Ю.М.Рабінович, М.С. Якир «Збірник задач і контрольних робіт з алгебри для 8 класу»- Х.:, Гімназія, 2010. – 96 с.
5. А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С. Якир «Збірник задач і контрольних робіт з геометрії для 8 класу»- Х.:, Гімназія, 2011. – 112 с.
6. Игра «Веришь- не веришь». -[Електронний ресурс]. – Режим доступу:

                          http://uchitmatematika.ucoz.ru/igra.doc 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток № 1.

 

Протокол журі

(таблиця оцінювання роботи команд в клубі «Що? Де? Коли?»)

 

Назва команди

Привітання

Розминка

Інформаційний конкурс

Конкурс капітанів

Розв'язування задач

Домашнє завдання

Підсумки

оригінальність

інформаційність

акуратність

1 вправа

2 вправа

3 вправа

оригінальність

научність

оформлення

Критерії

Кожний критерій – 4 б.

Сума балів за правильні відповіді

Сума балів

6 балів за 2 відповіді

12 балів

Кожний критерій – 4 б.

 

 

 

 

 

 

 

Додаток № 2