Урок (конспект+презентація) "Ознаки подібності трикутників. Розв’язування прикладних задач"

Тема уроку: Ознаки подібності трикутників. Розв’язування прикладних задач.

Мета уроку:формувати уміння застосовувати ознаки подібності трикутників при розв'язуванні  прикладних задач; розвивати пошукову пізнавальну активність учнів, логічне мислення, вміння міркувати, аналізувати і робити висновки, уяву, зв’язне мовлення;               виховувати наполегливість, впевненість у собі, любов та інтерес до математики; розширювати  кругозір учнів.

Тип уроку: урок практичного застосування знань, умінь, навичок.

Час проведення уроку: 90 хв.

Обладнання: мультимедійний проектор.

ХІД УРОКУ.

І. Організаційний момент.

ІІ. Мотивація навчальної діяльності.

(слайд 1)

Відомо, що в давнину люди спостерігали за світилами і вели календар; розраховували строки посіву, час розливу рік; орієнтувалися по зірках, прокладаючи маршрути морем і сушею. Усе це призвело до використання геометричних задач на практиці.

Сьогодні на уроці ми розглянемо деякі задачі практичного змісту. Розв’язуванням задач з використанням подібності трикутників займаються люди різних професій. Ці знання можуть знадобитися вам і в повсякденному житті. Все наше життя складається з маленьких проблем, які ми можемо вирішити, використовуючи ті знання, які отримуємо під час уроків.

III. Актуалізація опорних знань.

(слайд 2,3)

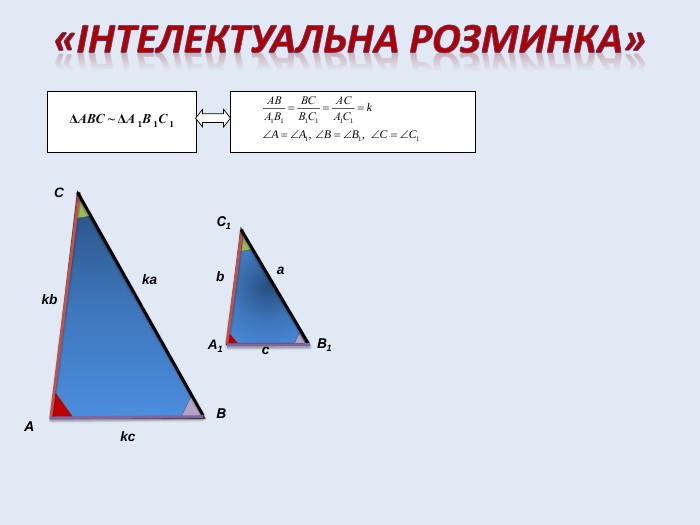
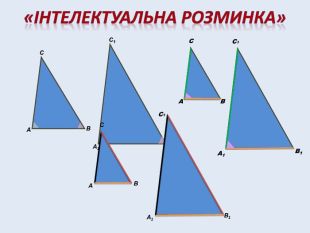
«Інтелектуальна  розминка». Повторення основних теоретичних фактів за питаннями:

1) які трикутники називаються подібними;

2)які геометричні твердження дозволяють встановити подібність трикутників;

3) сформулюйте першу ознаку подібності трикутників;

4) сформулюйте другу ознаку подібності трикутників;

5)сформулюйте третю ознаку подібності трикутників.

(слайд 4)

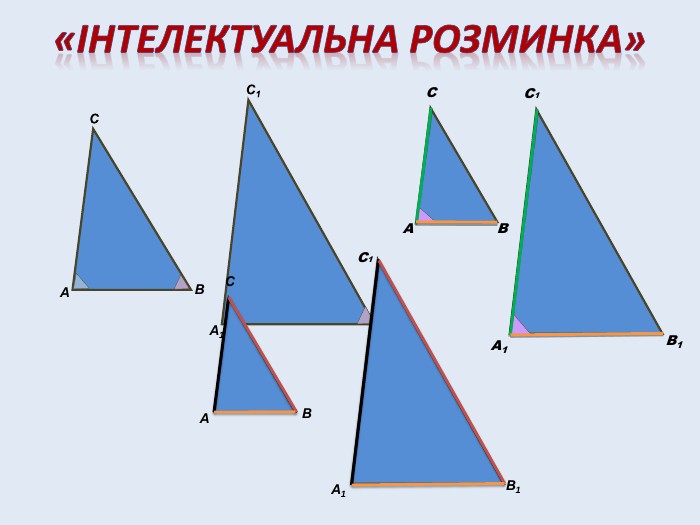
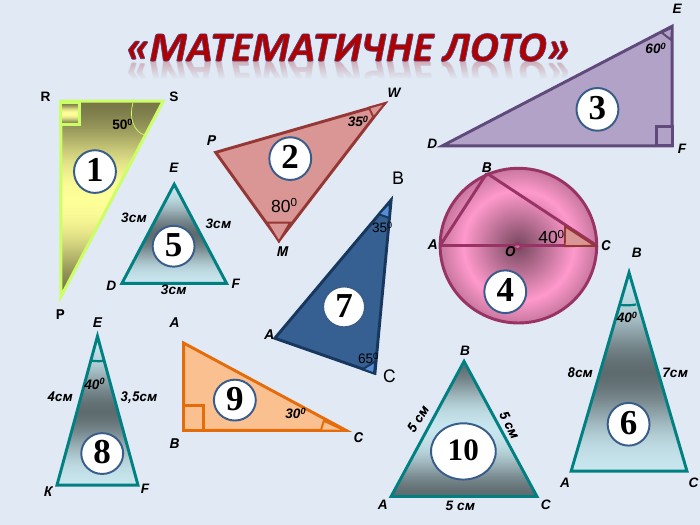
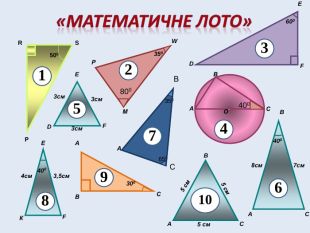
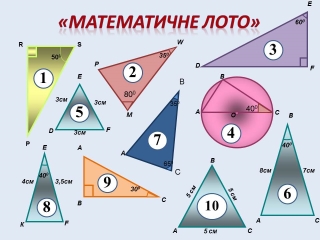
«Математичне лото». На слайді зображені трикутники. Знайти серед них пари подібних трикутників. Обґрунтувати свій вибір.

IV. Застосування знань. Розв’язування задач.

(слайд 5)

Завдання 1. Визначення висоти предмета.

Ви вирішили виміряти висоту дерева, це потрібно якщо ви, наприклад, вирішили спиляти дерево, яке знаходиться на вашій ділянці і заважає з якихось причин. Спиляти його не проблема, проблема в тому, чи не дістане воно до якоїсь будови, яка знаходиться недалеко від   дерева. Як же виміряти висоту дерева?

Висоту предмета можна визначити за допомогою тіні.

(слайд 6)

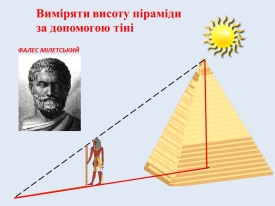Саме так Фалес знайшов геніальний по простоті спосіб виміряти висоту найбільшого з чудес світу - єгипетської піраміди Хеопса. Він визначив момент дня, коли тінь предмета по своїй довжині дорівнює його висоті. Вимірявши в цю годину тінь піраміди, Фалес отримав тим самим точне уявлення про її висоту.

Як ви думаєте, чому він зміг зробити такий висновок?

(Очікувана відповідь: прямокутні рівнобедрені трикутники подібні між собою.)

Чи обов’язково чекати на той час, коли тінь предмета по своїй довжині дорівнює його висоті? Спробуємо розв’язати задачі.

(слайд 7)

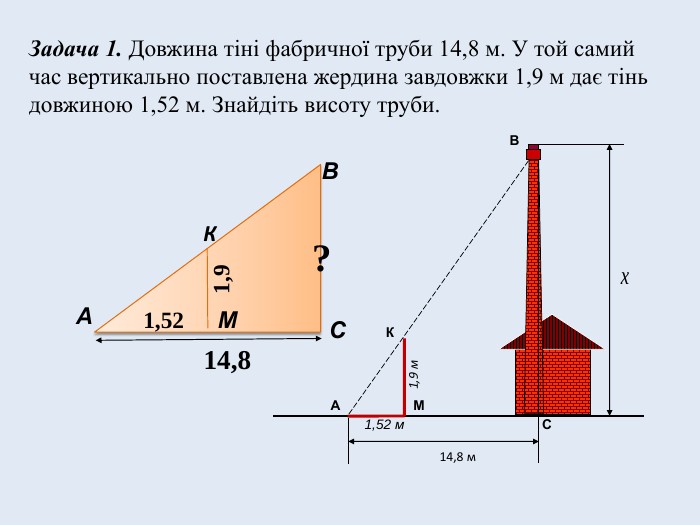
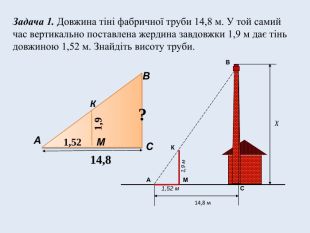
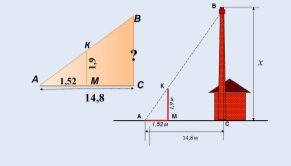Задача №1. Довжина тіні фабричної труби 14,8 м. У той самий час вертикально поставлена жердина завдовжки 1,9 м дає тінь довжиною 1,52 м. Знайдіть висоту труби.

Розв’язання.

РозглянемоАВС та АКМ:А–спільний, М=С=90⁰. Отже,                     АВС АКМ за першою ознакою рівності трикутників (два рівні кути).

, ,

Відповідь: 18,5 м  

(слайд 8)

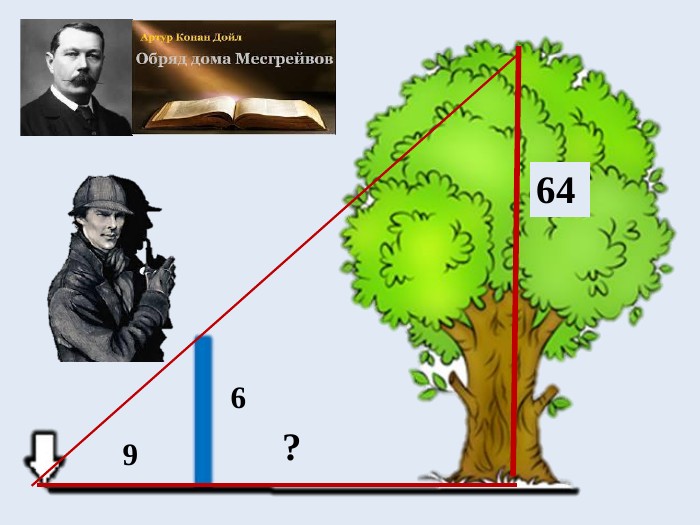
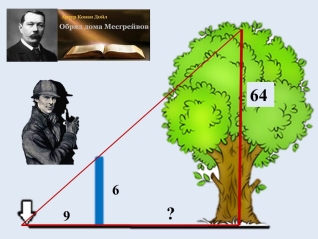Всесвітньо відомий письменник Артур Конан Дойль був лікарем. Проте він, напевне, дуже добре знав геометрію. В оповіданні “ Обряд родини Масгрейвів" він описав, як Шерлок Холмс розкрив страшний злочин у старовинному замку цього роду. Потрібно було визначити, де буде знаходитися кінець тіні в'яза, який давно зрубали. Та висота в’яза була відома - дерево мало висоту шістдесят чотири фути. Цей кінець вказував на вхід до підземелля, де були заховані скарби.

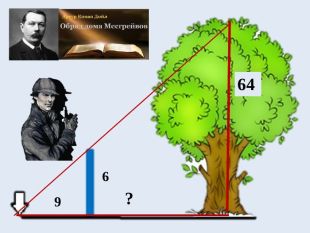
Ось як розповідає сам Шерлок Холмс: «Я зв'язав два вудлища — це дало мені шість футів,— і повернувся до того місця, де колись ріс в’яз. Сонце саме торкнулося верхівки дуба. Я закріпив вудлище вертикально, визначив напрямок тіні і виміряв її. Вона була дев'яти футів завдовжки.

Я взявся розраховувати далі. Якщо вудлище в шість футів завдовжки дає тінь в дев'ять футів, то дерево заввишки шістдесят чотири фути кидало б тінь довжиною в дев'яносто шість футів.»

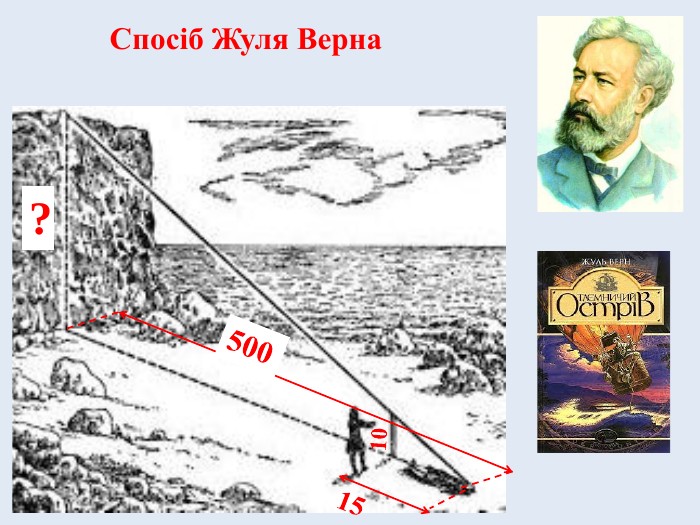
Висоту предмета можна визначати не тільки за допомогою тіні. Свій спосіб запропонував відомий письменник Жуль Верн в романі «Таємничий острів». Герої Верна вимірювали висоту скелі.

(слайд 9)

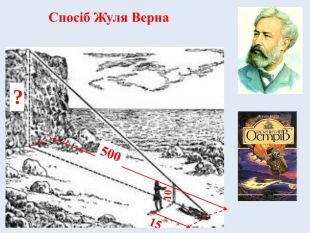
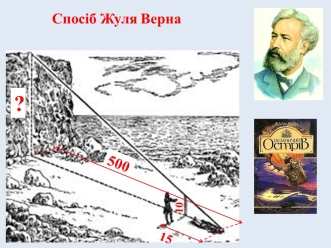«Зупинившись кроків за двадцять від краю моря і футів за п'ятсот від гранітної кручі, що зводилася перпендикулярно до водної гладі, Сайрес Сміт застромив жердину на два фути в пісок і за допомогою виска старанно виставив її перпендикулярно до лінії обрію. Після цього він одійшов і ліг на землю на такій відстані, щоб у полі його зору перебував верхній кінець жердини та гребінь гранітної кручі.»

Як ви можете пояснити дії героїв Верна?

(Очікувана відповідь: вони скористались подібністю трикутників.)

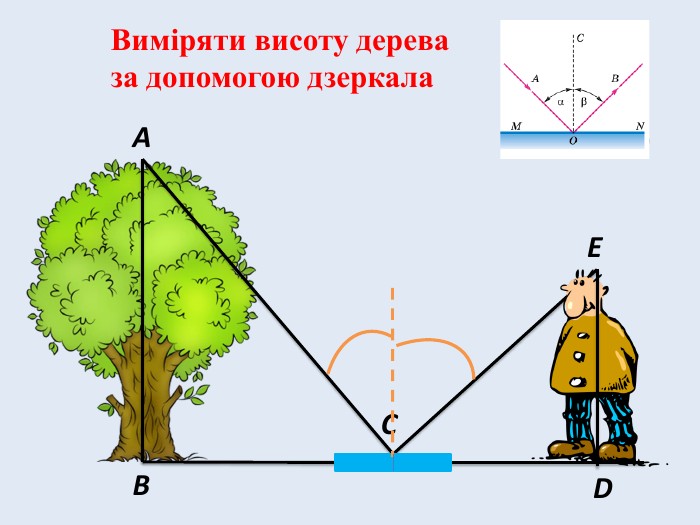
Висоту предмета можна визначити за допомогою дзеркала.

(слайд 10)

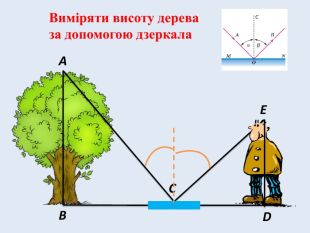
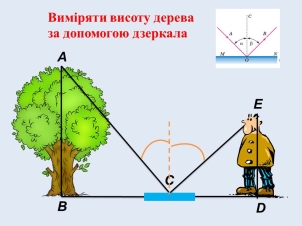В основі цього способу лежить закон відбивання світла. Вибираємо одиноке дерево і на деякій відстані від нього, на рівній поверхні, кладемо дзеркальце. Відходимо від нього назад так, щоб в дзеркальце було видно верхівку дерева. Дерево у стільки разів вище зросту спостерігача, у скільки відстань від дерева до дзеркальця більша за відстань від дзеркальця до спостерігача.

Спробуйте пояснити цей спосіб.

(Очікувана відповідь: Розглядаємо два трикутники: один з них утворений верхівкою дерева, основою стовбура і дзеркальцем, а другий — очами спостерігача, п'ятами ступнів і дзеркальцем. Вони подібні між собою.)

(слайд 11)

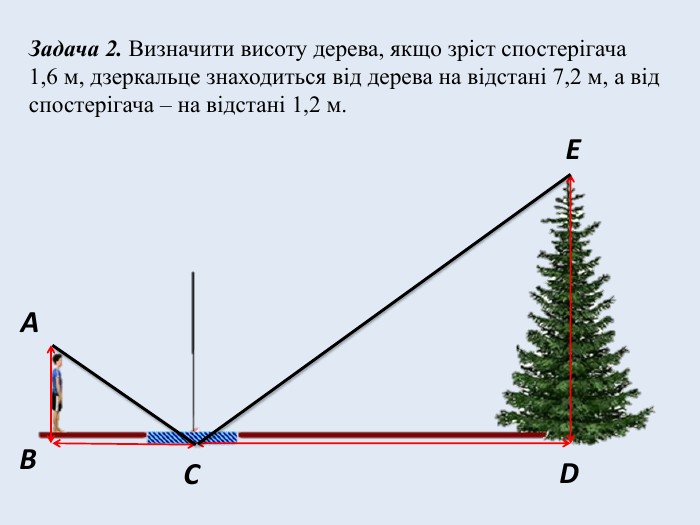
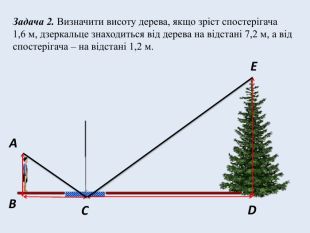
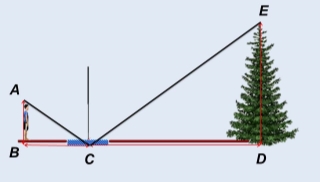
Задача № 2. Визначити висоту дерева, якщо зріст спостерігача  1,6 м, дзеркальце знаходиться від дерева на відстані 7,2 м, а від спостерігача – на відстані 1,2 м.

Розв’язання.

Точка С – дзеркало. За умовою BC = 7,2 м, CD = 1,2 м, DE = 1,6 м.  За законом відбивання світла кут падіння дорівнює куту відбивання. Маємо:

∠ECD = ∠ ACB,       Тоді  ΔECD ~ ΔACB.

 Тому   ,     ; AB = (1,6 ∙ 7,2) : 1,2 = 9,6 (м).

Відповідь: 9,6 м. 

(слайд 12)

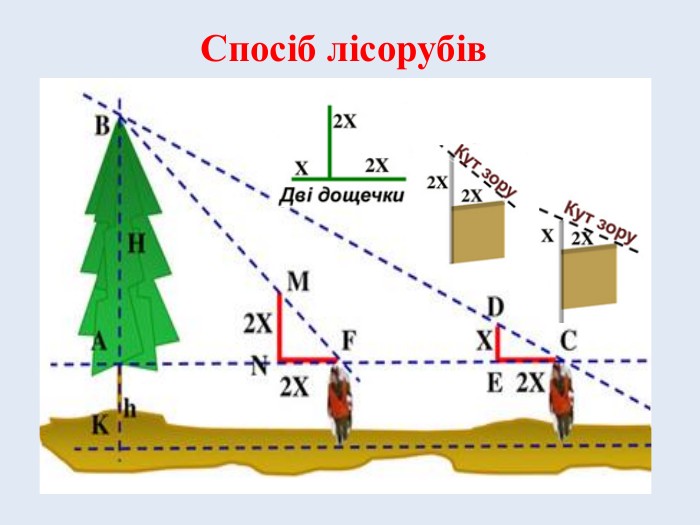
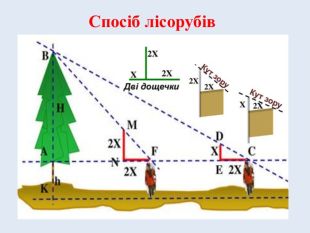
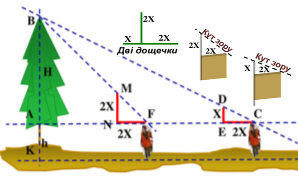Іноді неможливо виміряти великий об’єкт, бо він недоступний. Існує спосіб, який використовують лісоруби для визначення висоти дерев. Вони використовують прилад для побудови кута зору. Людина два рази, відповідно до малюнка, напрямляє кут зору для сполучення кінця приладу із верхівкою дерева.

(слайд 13)

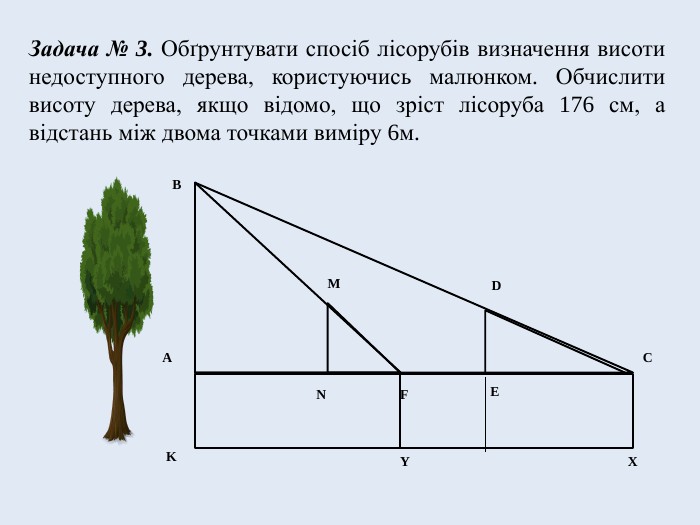
Задача № 3. Обґрунтувати спосіб лісорубів визначення висоти недоступного дерева, користуючись малюнком. Обчислити висоту дерева, якщо відомо, що зріст лісоруба 176 см, а відстань між двома точками виміру 6м.

  Розв’язання.

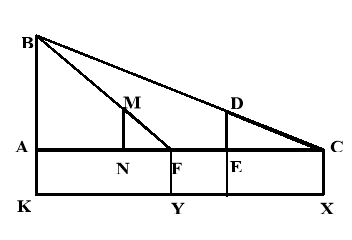
Отже, висота дерева

Відповідь: 7,76 м.

(слайд 14)

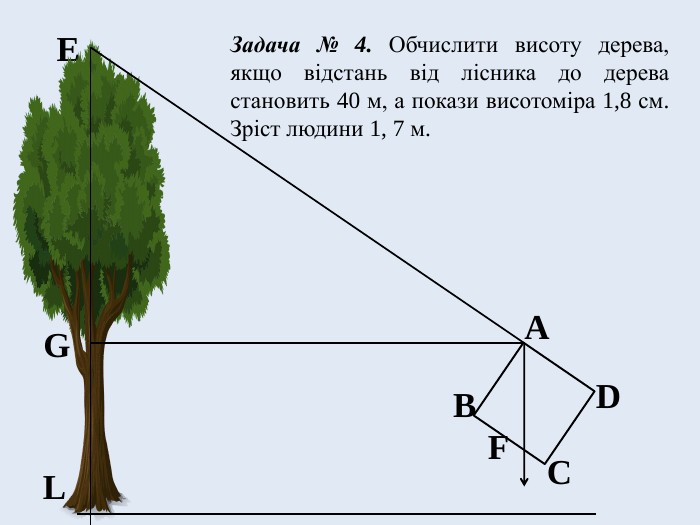
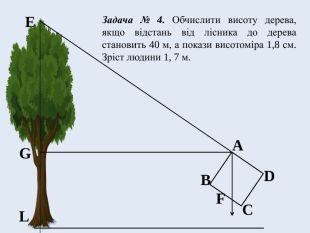
Задача № 4. Обчислити висоту дерева, якщо відстань від лісника до дерева становить 40 м, а покази висотоміра (опис приладу подано нижче) 1,8 см. Зріст людини 1, 7 м.

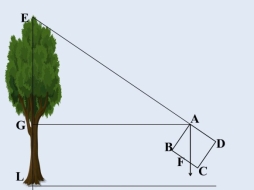Висотомір лісника являє собою квадратну пластинку розміром 10х10 см із закріпленою у точці А ниткою з підвішеним на ній тягарцем, яка під дією сили тяжіння завжди займає вертикальне положення, шкалою на стороні BС і візирами в точках A і D. Навівши за допомогою візирів сторону AD на вершину дерева E і відмітивши покази BF на шкалі, які показує нитка з тягарцем, лісник за допомогою нескладних обчислень знаходить висоту дерева.

Розв’язання.

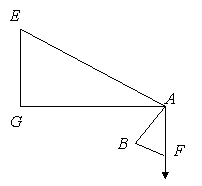
          За умовою AG = 40 м = 4000 см, BF = 1,8 см, AB =10 см.

∠ GEA = ∠ AFB  (оскільки прямі GE і AF, DE і BC паралельні)

∆EGA ~ ∆FBA (за двома кутами), тому

  ,      

Отже, висота дерева становить 7,2 + 1,7 = 8,9 (м).

Відповідь: 8,9 м.

(слайд 15)

Розв’язання окремих старовинних завдань практичного характеру можуть знайти застосування і в наш час, а тому заслуговують на увагу. Історія геометрії зберігає чимало прийомів розв’язування задач на знаходження відстаней. Визначення відстаней до кораблів, що знаходяться в морі, - одне з таких завдань.

(слайд 16)

Задача № 5. Визначити відстань від берега до корабля в морі, знаючи висоту щогли  - 20 м, довжину великого пальця - 4 см, відстань від очей до руки - 60 см.

Розв’язання.

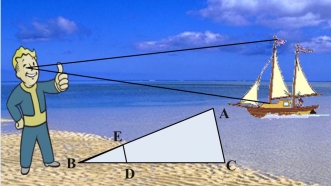Нехай корабель знаходиться в точці A, а спостерігач у точці B. Потрібно визначити відстань BC. Висота щогли – відома величина для певного корабля. Палець слід розташувати паралельно до щогли, виміряти відстань від очей до руки, довжину великого пальця.

∆ AВС ~ ∆ EВD (за лемою про подібні трикутники або за першою ознакою подібності трикутників), звідси ВС : BD = AC : ED.

Нехай ВС = x м, тоді    

Відповідь: 300 м.

(слайд 17)

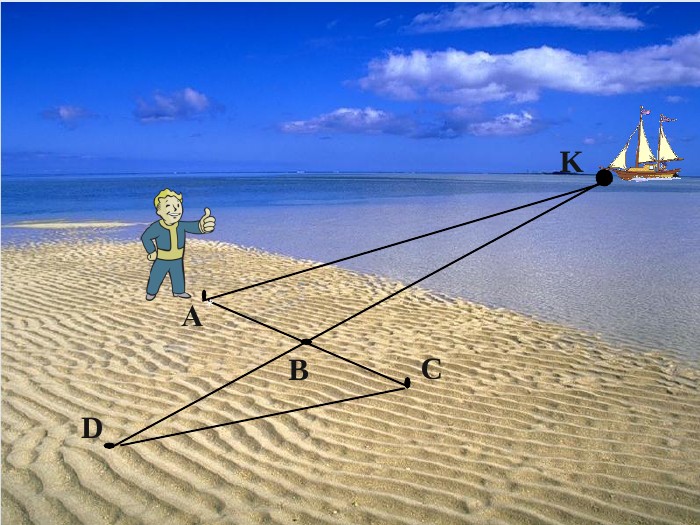
Існують інші способи визначення відстані до корабля у морі. Нехай корабель знаходиться в точці К, а спостерігач в точці А. Потрібно визначити відстань АK. Побудувавши в точці А прямий кут, необхідно відкласти на березі два відрізка АВ та BC. У точці С знову побудувати прямий кут, причому спостерігач повинен йти по перпендикуляру  до тих пір, поки не дійде до точки D, з якої корабель К  і точку В буде видно на одній прямій. Прямокутні трикутники ВСD та ВАК подібні (за двома кутами). Відстані ВС, АB, CD вимірюємо, AК знаходимо з пропорції.

Одним з видів задач на визначення відстані до недоступного об'єкта є практична задача на знаходження ширини річки. Існує багато способів це зробити. Ми розглянемо декілька з них.

(слайд 18)

Для пластунів («Пласт» — національна скаутська організація України) існує така інструкція: «Щоб оцінити ширину річки, вибери собі якийсь предмет А на протилежному березі навпроти твого положення В. Йди під прямим кутом до точки D уздовж берега, скажімо, 90 ярдів. Перейшовши 60 ярдів, постав там палицю чи камінь, як точку C. Дійшовши до точки С, 30 ярдів від точки C і 90 ярдів від точки B, повернись знов під прямим кутом і йди від річки, рахуючи кроки, аж поки не побачиш своєї палиці й дерева на протилежному березі річки на одній лінії. Число кроків, що ти пройшов від берега річки, тобто відстань DE, дорівнюватиме половині ширини річки АB.»

Спробуйте пояснити цей спосіб.

(Очікувана відповідь: Розглядаємо два трикутники:ABC та EDC. Вони подібні між собою за двома кутами. За умовою сторона BC вдвічі більша за CD, тому ширина річки AB вдвічі більша за відстаньDE.)

(слайд 19)

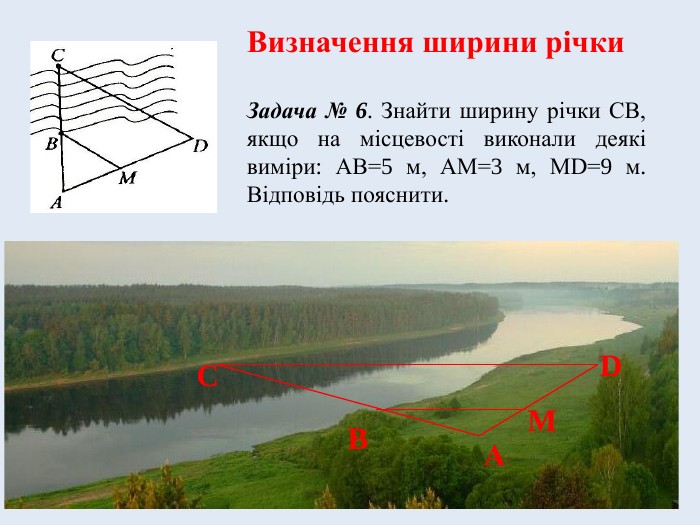
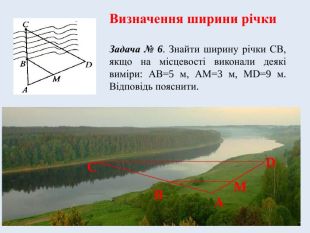
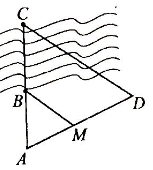
Задача № 6. Знайти ширину річки СВ, якщо на місцевості виконали деякі виміри: АВ=5 м, АМ=3 м, МD=9 м. Відповідь пояснити.

Розв’язання.

∆ AСD ~ ∆ AВM (за лемою про подібні трикутники або за першою ознакою подібності трикутників), звідси ВA : CA = AM : AD.

Нехай AС = x м, тоді    

    ВC=AC- ВA =20-5=15  

Відповідь: 15 м.

(слайд 20)

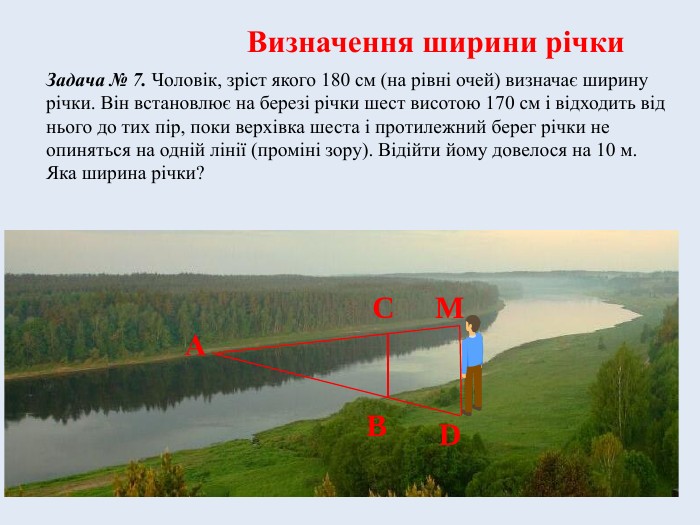
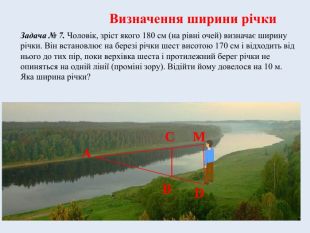
Задача № 7. Чоловік, зріст якого 180 см (на рівні очей) визначає ширину річки. Він встановлює на березі річки шест висотою 170 см і відходить від нього до тих пір, поки верхівка шеста і протилежний берег річки не  опиняться на одній лінії (проміні зору). Відійти йому довелося на 10 м. Яка ширина річки?

Розв’язання.

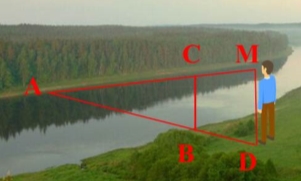
∆ AMD ~ ∆ ACB (за першою ознакою подібності трикутників), звідси

 AB : AD = BC : MD.

Нехай AB = x м, тоді   

Відповідь: 170 м.

(слайд 21)

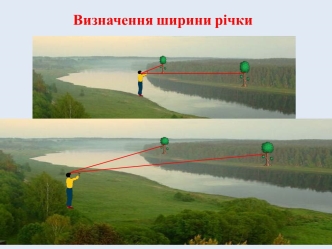
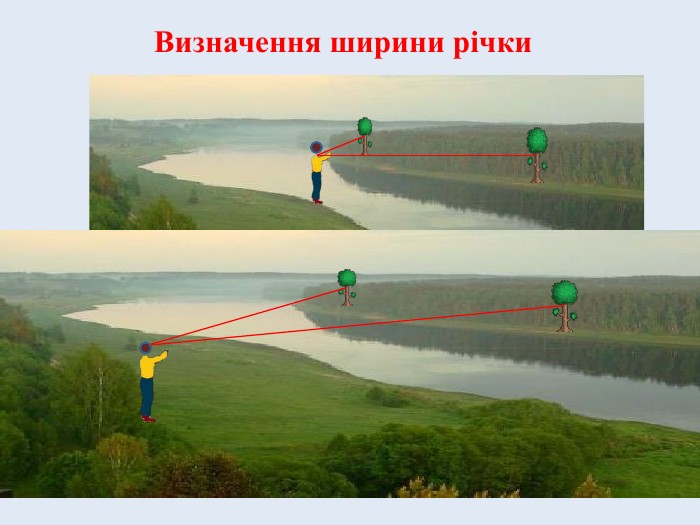
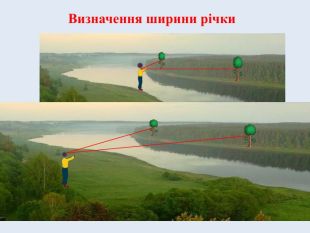
На Україні існував і інший цікавий метод вимірювання ширини річки. У витягнуту руку брали травинку такої довжини, щоб вона закрива­ла проміжок між двома орієнтирами, які видно на протилежному березі. Потім потрібно скласти травинку навпіл і відійти так, щоб відстань між орієнтирами закривалася тепер половинкою довжини травинки. При цій умові ширина річки дорівнюватиме відстані між першим і другим місцем знаход­ження людини, яка вимірює.

(слайд 22)

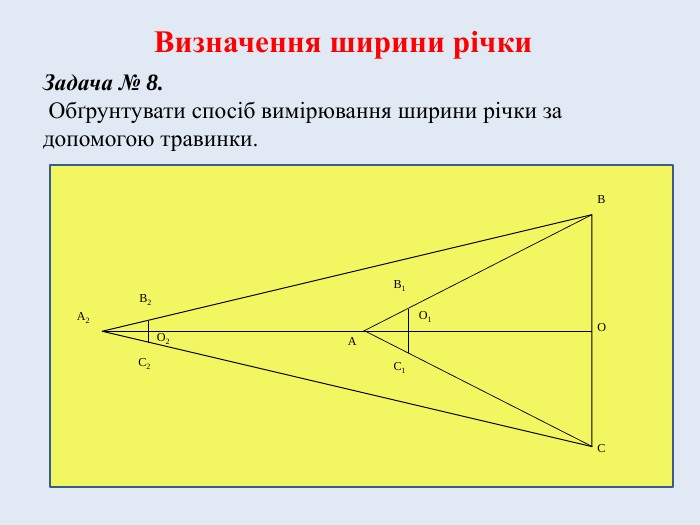
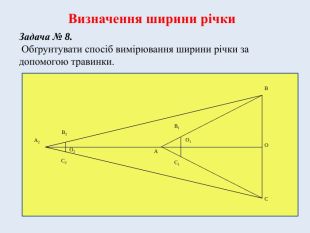
Задача № 8. Обґрунтувати спосіб вимірювання ширини річки за допомогою травинки.

Розв’язання.

Доведемо дане твердження. Для цього побудуємо рисунок. Позначимо ширину річки АО = х; відстань, яку пройшла людина AA = l;  відстань від очей до  травинки АО=AО= l; довжину травинки В₁С₁= d; відстань між деревами ВС=Н.

Тоді з подібності трикутників ABC і АВС за двома кутами маємо .

Аналогічно, для трикутників АВС і АВС- виконується рівність .

 3 цих рівнянь х+ l =2х , х= l, що і потрібно було довести.

(слайд 23)

V. Рефлексія. Підбиття підсумків уроку.

Ми з вами вивчаємо одну з найцікавіших тем геометрії «Подібність трикутників». Чому найцікавіших? Тому,  що знання подібності трикутників і їх властивостей допомагає в найнесподіваніші моменти.  

Давайте підведемо підсумки уроку. Подумайте і скажіть, чи дізналися щось нове, чому навчилися?

 (Очікувані відповіді: розв’язувати задачі на подібність трикутників; знаходити висоту предмета; обчислювати ширину річки; розв’язувати практичні задачі)

Можна зробити висновок, що використовуючи ознаки подібності трикутників ми можемо розв’язати ряд практичних задач.

Сьогодні на уроці ми розглянули задачі, пов'язані з геометричними вимірюваннями на місцевості - визначенням висоти предмета, знаходженням відстані до недоступних предметів. Наведені завдання мають значний практичний інтерес, закріплюють отримані знання з геометрії і можуть використовуватися у різних життєвих ситуаціях.

Думаю, ви переконались у справедливості слів відомого римського філософа і державного діяча Луція Сенеки : «Ми навчаємось не для школи, а для життя».

(слайди 24, 25, 26)

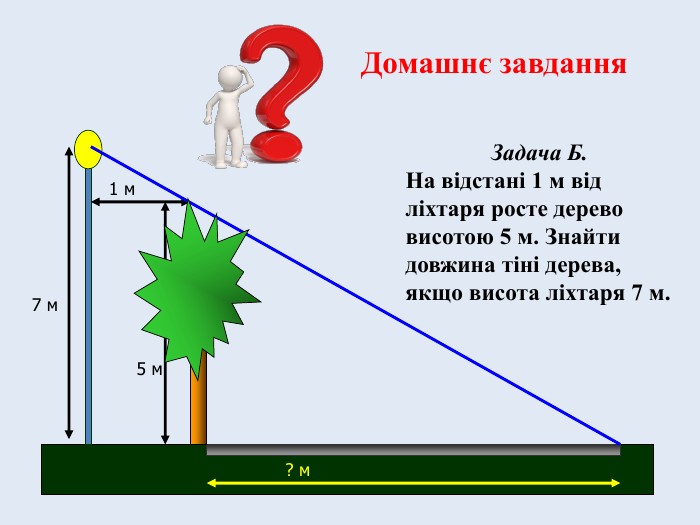
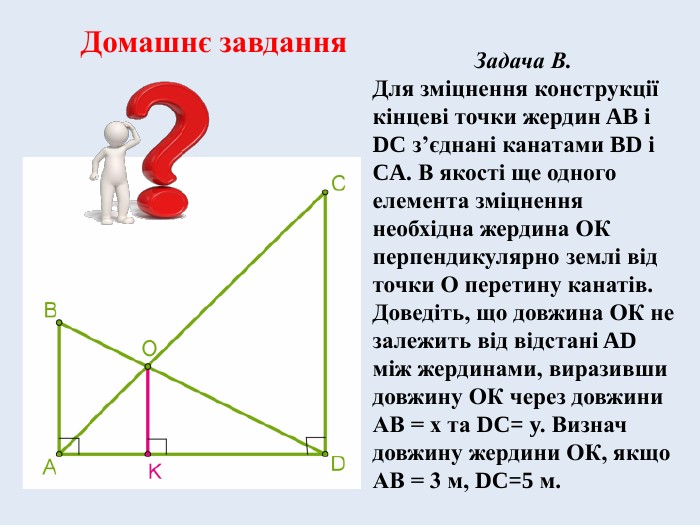
VІ. Домашнє завдання. 

Розв’язати задачу, самостійно обравши рівень складності.

Додаткові задачі, які можна використати при проведенні уроку.

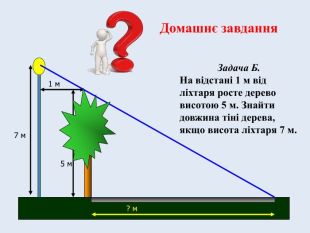
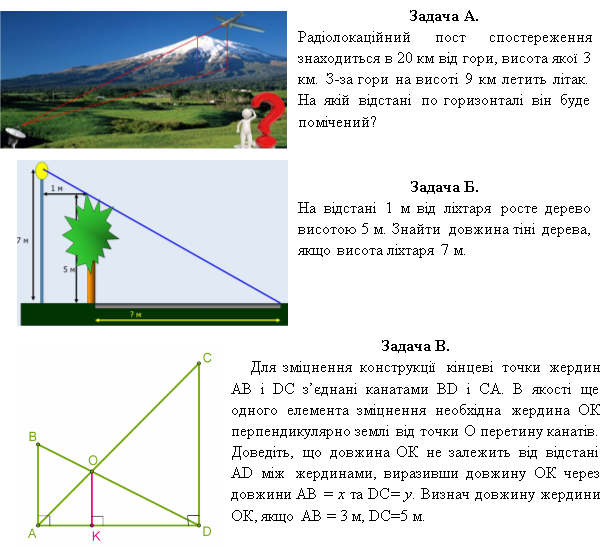
Задача 1.

У місті встановлено високий пам’ятник. Є фотографія цього пам’ятника. Як можна скористатися цим знімком для визначення висоти пам’ятника? 

Cпосіб практичного розв’язання.

Для приблизного знаходження висоти пам’ятника за знімком можна вибрати дві точки, розташовані біля фундаменту цього пам'ятника, і виміряти відстань між ними на фотографії  і на місцевості. Знайшовши відношення k першої  відстані до другої, ми дізнаємося масштаб знімка, після чого залишиться заміряти на знімку висоту пам’ятника і поділити її на k.

Задача 2.

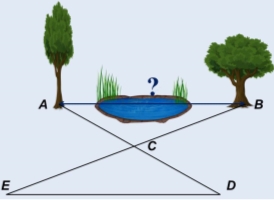Необхідно виміряти на місцевості відстань між двома об'єктами, розділеними  перешкодою, що не дозволяє безпосередньо прокласти пряму між цими об'єктами. Як можна зробити таке вимірювання? Обчислити відстань AB, якщо AC = 48 м, DC = 192 м, DE = 168 м.

Cпосіб практичного розв’язання.

Нехай  А і В - дані точки на місцевості, між якими визначається відстань. Виберемо точку С, з якої видно обидві точки А і В. На продовженні відрізка АС за точку C позначимо точку D на довільній відстані від точки С. Будемо рухатись від точки  D паралельно  АВ до тих пір, поки точка  Е (спостерігач) не опиниться на одній прямій із точками В і C. Тоді трикутники ABC і DEC будуть подібні. Звідси можна обчислити відстань AB.

∆ АВC ~  ∆DEC (за двома кутами). Звідси AB : DE = AC : DC;   

AB : 168 = 48 : 192.   Звідси маємо:  AB = (168 ∙ 48) : 192 = 42 (м). 
Відповідь: 42 м. 

Задача 3.

Як виміряти глибину котло­вану, якщо у вас немає   мотузки?

Cпосіб практичного розв’язання.

Глибину котловану можна виміряти за допомогою короткої палки. Для цього потрібно знайти очима на дні котловану який-небудь орієнтир О і, ставши на край обриву, розташувати палку горизонтально таким чином, щоб основа В палки розташувалась на одній вертикалі з очима Н, а другий її кінець опинився на лінії орієнтир — очі спостерігача.

Потім лягаємо на край обриву і повторюємо свої дії: опускаємо основу палки по вертикалі нижче краю котловану. Вимірявши відстані HB=в і FC=с від очей до основи палки в першому і в другому положенні відповідно  та знаючи свій зріст до рівня очей FH=h, можна обчислити глибину x=FD котловану. Дійсно, позначимо через у=OD відстань по горизонталі від орієнтиру до проекції краю обриву, довжину палки BA=CN=a.  

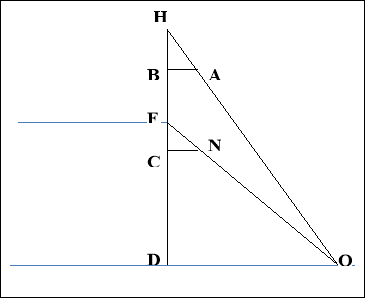
Тоді з подібності трикутників HDO і HBA   маємо .

Аналогічно, для трикутників FDO і FCN- виконується рівність .