Задачі на побудову лише односторонньою лінійкою

Задачі на побудову лише односторонньою лінійкою

Задачі на побудову сьогодні рідко розв’язуються у шкільному курсі. Подібну ситуацію ми бачимо на олімпіадах з математики різного рівня. Отже, ми знову повертаємось до цікавих і складних задач на побудову, які захоплювали математиків не одне тисячоліття.

У цій статті розв’яжемо ряд задач на побудову лише геометричною (односторонньою) лінійкою. За допомогою лінійки ми можемо проводити фіксовану пряму через дві різні точки або довільну пряму через дану точку.

Лінійка є найпростішим інструментом серед тих, які використовують при виконанні задач на побудову. Зокрема це: циркуль, лінійка з двома паралельними краями, рухомий кут ( прямий або довільний); сталий відрізок, трисектор, бісектор і різні криві. На практиці, інколи, легше використовувати лінійку, ніж циркуль, хоча при цьому збільшується кількість основних операцій. Так, наприклад, у практиці геодезиских робіт доводиться проводити лише прямі лінії. У теорії перспективи проведення прямих ліній відіграє важливу роль.

Теорію розв’язування задач на побудову лише однією лінійкою розвинув німецький математик, філософ, фізик і астроном Ламберт Йоганн Генрих (1728-1777). Цю теорію він називав геометрією лінійки. Він зазначав, що хоч при застосуванні лише лінійки розв’язування задачі дуже довге, проте в інженерній та землемірній практиці вигідніше застосовувати лише один цей інструмент.

Геометрію лінійки розвивали також: французькі математики - Ш.Ж. Бріаншон (1785-1864) і Ж.В. Понселе (1788-1867).

Звичайно, задач, які будуються лише за допомогою однієї лінійки набагато менше ніж тих, які будуємо за допомогою циркуля і лінійки.

Понселе був перший, хто на практиці висловив таку думку: «Щоб розв’язати задачу на побудову лише однією лінійкою треба, щоб на площині було побудоване коло з заданим центром». Цю думку розвивав Я. Штейнер (1796-1863) – швейцарський математик. Він розглядав побудови, які можна виконати за допомогою прямих ліній, коли на рисунку дано одну з допоміжних фігур:1) дві паралельні прямі; 2) паралелограм; 3)квадрат;

 4) коло і його центр.

Я. Штейнер довів теорему: «Довільну задачу на побудову другого степеня можна розв’язати за допомогою лише проведення прямих ліній, якщо є побудоване довільне коло і його центр».

Наявність центра обов’язкова. Д.Гільберт (1862-1943) – німецький математик довів, що коли дано коло, а центра його не дано, то побудувати центр за допомогою лише лінійки не можливо.

Проте замість кола Штейнера можна задати інші криві другого порядку, наприклад еліпс з його центром і одним з фокусів. Центр потрібний для проведення паралелей, а фокус – для проведення перпендикулярів.

При розв’язанні задач на побудову лише однією лінійкою часто використовують базову задачу: «Пряма, яка проходить через точку перетину діагоналей трапеції і через точку перетину її не паралельних сторін, ділить пополам основи трапеції.

Доведення

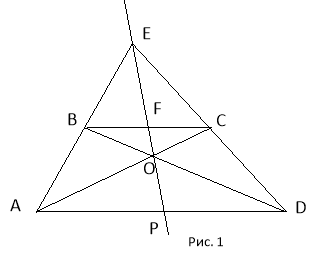1.                    ∆АЕР∆BEF, тому 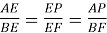(1)
2.                    ∆РDE∆FCE, тому (2)

З рівносте (1) і (2) маємо:

, або (3)

3.                    ∆АРО∆СFО, тому (4)
4.                    ∆OРD∆ОFB, тому 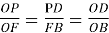(5)

З рівносте (4) і (5) маємо:

, або (6)

Перемножимо рівність (3) і (6):

, тому АР=DP.

З рівності (6) маємо , тому CF=FB.

Застосуємо цю задачу до розв’язування інших задач.

Задача 1. Точка К – середина відрізка АВ. Через точку D провести пряму, паралельну АВ.

Побудова

 

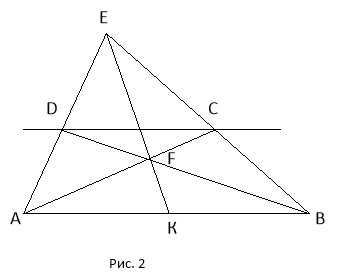Будуємо пряміAD, BD, BE i KE (Е – довільна точка прямої AD).

Нехай КЕ перетинає пряму DB у

точці F.

Будуємо пряму AF, яка перетне пряму   ВЕ у точці С. Пряма DC||АВ.

 

 

 

 

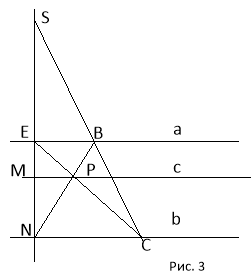Задача 2. Задано дві паралельні прямі а і b  і точку М. Через точку М провести пряму С паралельну прямим а і b.

Нехай точка М лежить між прямими а і b. Через довільну точку N прямої b будуємо пряму MN.

Через довільну точку S прямої MN будуємо пряму. Через довільну точкy прямої будуємо пряму, яка перетинає прямі а і b відповідно в точках В і С. будуємо діагоналі трапеції BCNE. Маємо точку Р. Пряма МР (пряма с) шукана.

 

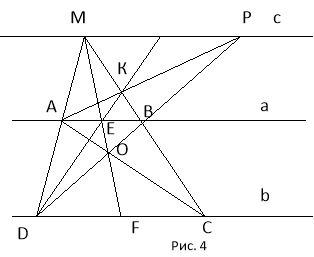
Якщо точка М лежить зовні прямих а і b, то через точку М будуємо дві прямі, які перетинають прямі а і b відповідно в точках А і В та С і D. АВСD – трапеція, О – точка перетину її діагоналей. Пряма МО перетинає пряму а в точці Е. Будуємо пряму DE. Маємо точку К. Прямі АК і DO перетинаються в точці Р, яка є шуканою. Пряму МР (пряму с) побудовано.

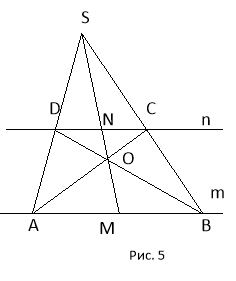Задача 3. Прямі  m i n паралельні. Поділити пополам відрізок АВ, який лежить на прямій m.

Побудова:

Через довільну точку S площини проводимо прямі SА і SВ, які перетинають пряму n у точках D і С. Будуємо АС і ВD. Маємо точку O. Будуємо пряму SО, яка пройде через середину відрізка АВ.

 

 

Задача 4. Дано дві паралельні прямі а і b і на прямій а відрізок АВ. Збільшити відрізок АВ в n раз ( n- натуральне).

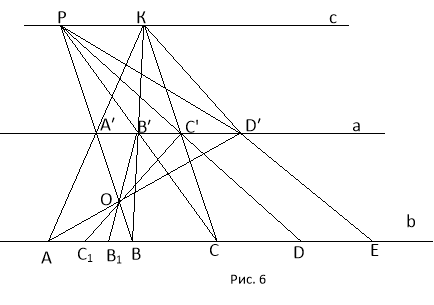Побудова:

Через довільну точку К, яка розміщена за прямими, проводимо пряму с паралельну а і b (Див. задача2)

Будуємо прямі АК і ВК, які перетинають пряму а відповідно в точках А і В′. будуємо пряму ВA′, яка перетинає пряму с у точці Р і пряму РВ′, яка перетне пряму b у точці С.

 Тоді АВ=ВС. Будуємо пряму СК. Маємо точку С′. Пряма РС' перетне пряму у точці D.

Тоді АВ=ВС=СD і т.д.

Рис. 6 дозволяє поділити відрізок АВ на n рівних частин. Для прикладу n=3. Потроїмо відрізок АВ. Одержимо точки А′, В′, С′ і D′, причому А′В′=С′В′=С′D′. Будуємо прямі А і В, які перетнуть в точці О. через точку О проводимо прямі В₁, С₁. Точки С₁ і В₁ поділили відрізок АВ на три рівні частини.

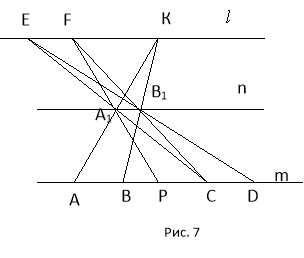
Задача 5. Дано дві паралельні прямі m i n. На прямій m побудовано відрізок АВ і точку С. Побудувати відрізок СD. рівний відрізку АВ.

Побудова

Через довільну точку К, яка лежить поза прямими m i n, проведемо пряму l, паралельну прямим m i n.

(Див. Задача 2).

 

 

 

Будуємо прямі КА і КВ. На прямій n  одержали точки А₁ і В₁. Через ці точки і точку С проведемо прямі, які перетнуть пряму l у точках Е і F.

Прямі FА₁ і ЕВ₁ перетнуть пряму m у точках Р і D. Відрізки СР і СD  дорівнюють відрізку АВ. Задача має два розв’язки.

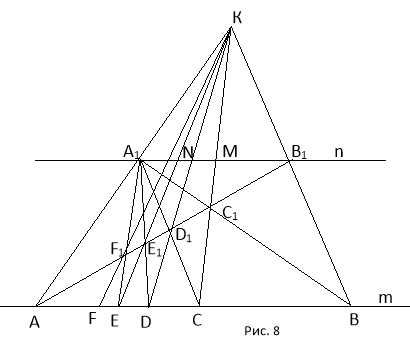Задача 6. Задано дві паралельні прямі m i n. На прямій m побудовано відрізок АВ. Побудувати відрізок АВ ( n – натуральне число, n>1)

Побудова

Базова задача дозволяє побудувати АВ, тобто поділити відрізок пополам.

Нехай n=3. Через довільну точку К, яка лежить поза прямими m i n, проведемо прямі КА і КВ, які перетнуть пряму  n в точках А₁ і В₁. Потім будуємо прямі АВ₁ і ВА₁, які перетнуться в точці С₁.

 

Пряма СА₁ і АВ₁ перетинаються у точці D₁. Через точки С₁ і D₁ будуємо прямі КС₁ і К D₁, які перетинають відрізок АВ у точках С і D. Доведемо, що АD = .

1.                    ∆АDD₁∆B₁ND₁,

тому (1)

2.                    ∆DD₁C∆ND₁A₁, тому

  (2)

З рівносте (1) і (2) маємо:

, або (3)

Аналогічно з подібності відповідних трикутників встановлюємо, що

  (4).

З рівностей (3) і (4) маємо: або (5)

AD=AC-DC (AC=BC), тому AD=BC-DC.

Виконаємо підстановку у рівність (5):

(DB=DC+CB), тому

 ,

, або ВС=3 , а ВD=4 .

Значення BD  підставимо у рівність (5).

, .

АВ=2ВС=6. Отже відрізок АD = ;

Аналогічно провівши відрізок А₁ отримаємо точку E₁. Пряма КЕ₁ перетне відрізок АВ у точці Е. АЕ=.

Аналогічно будуємо точку F таку, що АF=.

Доведення останніх двох рівостей здійснюється аналогічно.

Продовживши побудову, можемо знайти , і т.д. частину відрізка АВ.

Подібне доведення було запропоновано французьким математиком Ш.Ж. Бріаншоном.

Він розглядав повний чотирикутник A₁D₁C₁K і приходив до висновку, що точки А, С, Dі В, розміщено гармонійно, отже AD:DC=AB:BC. Але АВ=2ВС, тому з попередньої рівності маємо, отже АD = .

Задача7. Дано дві паралельні прямі m i n. На прямій m побудовано відрізок АВ. На прямій m побудовано відрізок, відношення якого до відрізка АВ дорівнює відомому раціональному числу.

Побудова. Нехай це число буде , де m i  n – натуральні числа.

Відрізок АВ ділимо на n рівних частин (задача 5) і відкладаємо n-ну частину m раз.

Існує багато цікавих задач на побудову лише лінійкою, якщо додатково побудовано: паралелограм; квадрат; два паралельні відрізки відношення яких відоме; коло з його  центром і т.ін.