Широкова Олена Анатоліївна вчитель математики

Дніпровський ліцей № 111 ДМР

Тема: Координатнаплощина

Цілі:

-       навчальна: ввести поняття координатна площина, координати точки;

-       розвивальна: розвивати увагу, формувати просторове та логічне мислення, пам’ять;

-       виховна: виховувати інтерес до вивчення математики, старанність, працьовитість.

Очікувані результати: учні повинні вміти креслити систему координат, знаходити координати точки, за заданими координатами вміти побудувати точки.

Тип уроку: урок засвоєння нових знань.

Обладнання: мультимедійний проектор, креслярське приладдя, роздавальний матеріал.

Хід уроку

1.    Організаційний етап.

2.    Мотиваційний етап.

Людина постійно вивчає світ навколо себе, вигадує та застосовує нові винаходи. Одним з таких винаходів є 3D-принтер.

3D-принтер — пристрій, що використовує метод пошарового створення фізичного об'єкта за цифровою 3D-моделлю. 3D-моделювання має великій простір для застосування. Так, наприклад, для друку органів придумали біопринтер — пристрій, в якому зі стовбурових клітин друкується 3D-структура майбутнього об'єкта (органу для пересадки). В будівництві за допомогою 3D-принтерів велетенського розміру друкують будинки з бетону. 3D-принтер застосовують коли друкують карбонові деталі для космічної промисловості. 3D-принтер також знайшов застосування в протезуванні кінцівок людини.

Все перелічене спирається на знаннях теми, з якою ми сьогодні познайомимося. Ця тема називається “Координатна площина”.

3.    Етап вивчення нового матеріалу.

Декартову систему координат вперше запропонував відомий французький математик Рене Декарт близько 1637року в праці «Геометрія», одному з додатків до видатного філософського твору «Міркування про метод». Аналогічний принцип можливо застосовувати для визначення положення будь-якої точки у тривимірному просторі за допомогою трьох впорядкованих декартових координат.

Прямокутна система координат на площині утворюється двома взаємно перпендикулярними осями координат X і Y . Осі координат перетинаються в точці O , яка називається початком координат. На кожній осі вибрано додатний напрям та одиничний відрізок. Осі координат ділять площину на чотири координатні чверті (I, II, III, IV). Пропоную переглянути відео:

https://drive.google.com/file/d/1-jKeh43xO5RgVYWR42XHkW1POzyDmLp2/view?usp=drive_link

Для закріплення матеріалу дамо відповіді на наступні питання:

1.    Яким чином утворилась прямокутна система координат?

2.    Яку точку називають початком координат?

3.    Що таке координатні чверті?

4.    Як позначають додатний напрям осі координат?

5.    Що таке одиничний відрізок?

6.    Скільки координат на площині визначають положення будь-якої точки?

7.    Як визначити координати точки в прямокутній системі координат?

8.    Яке практичне застосування має тема “Координатна площина”? Відповіді:

1.    Координатна площина утворилась внаслідок перетину двох координатних вісей під кутом 90 градусів.

2.    Точку перетину координатних вісей називають початком відліку і позначають буквою О (0;0).

3.    Координатні вісі ділять площину на чотири координатні чверті (I, II, III, IV).

4.    Для позначення додатного напрямку вісей використовують стрілку.

5.    Довжина відрізка прийнята за одиницю довжини називається одиничним відрізком.

6.    Дві координати х і у на координатній площині визначають координати будь-якої точки.

7.    Для того, щоб визначити координати точки, проводять з цієї точки перпендикуляри до координатних вісей Х та У. Отримані таким чином числові значення і будуть відповідною координатою.

8.    Найпростішим прикладом використання системи координат є глядацька зала. Де номер ряду і номер міста є координатами. Географічні широта та довгота є прикладом не прямокутної системи координат.

4. Етап формування практичних навичок Задача № 1. Визначте координати точки А.

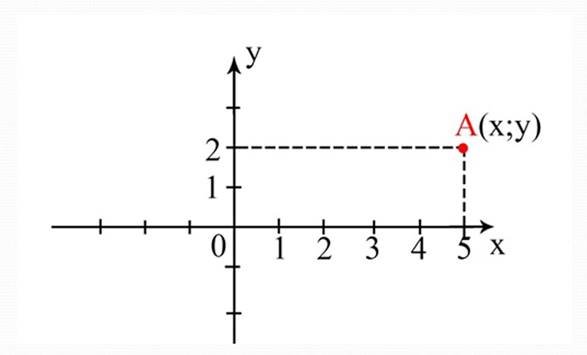
Відповідь: Точка А (5;2).

Задача № 2. Визначте координати точок А, В,С.D, E, F.

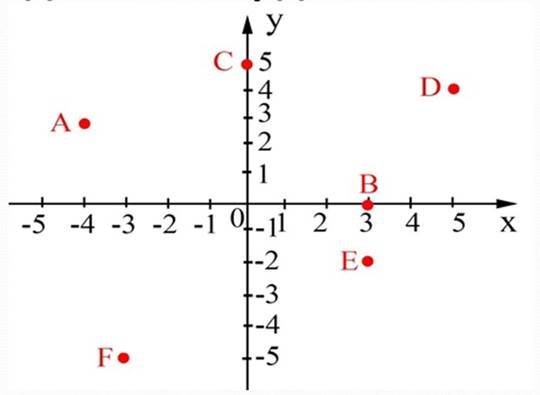
Відповідь: А(-4;3), В(3;0), С(0;5), D(5;4), E(3;-2), F(-3;-5).

Задача № 3. Визначте координати вершин трикутника АВС.

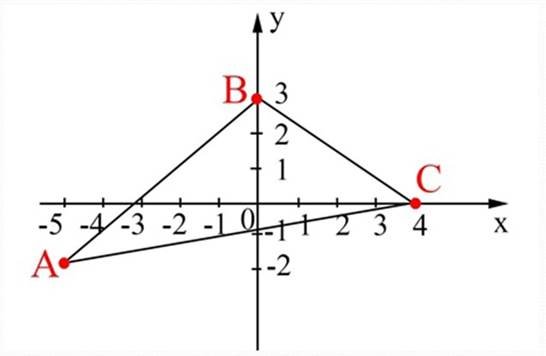
Відповідь: А(-5;-2), В(0;3), С(4;0).

Задача № 4. В одній координатній площині побудуйте точки:

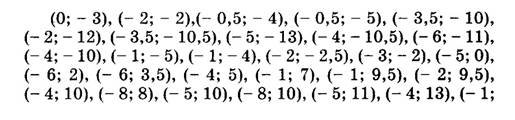
Послідовно з’єднуючи всі точки отримаєте малюнок.

Відповідь: за QR- кодом