Урок "Квадратична функція"

Про матеріал

урок з алгебри "Квадратична функція" для учнів 9 класу з елементами інтерактивних технологій та методів

Перегляд файлу

Тема. Квадратична функція, її графік та властивості.

Мета: узагальнити і систематизувати знання учнів з даної теми, вдосконалити навички побудови графіка квадратичної функції, вміння проводитиелементарне дослідження функції; показати застосування квадратичної функції.

Обладнання: плакат із графіками квадратичної функції, комп стерна презентація на тему «Функція», «Квадратична функція», зошити, підручник, канцелярські прилади, картки.

Тип уроку: узагальнення і систематизації знань.

Хід уроку.

І. Організаційний момент:

Мотивація навчальної діяльності учнів;

Повідомлення теми, мети уроку.

ІІ. Перевірка домашнього завдання.

Даються відповіді на запитання, що виникли в учнів під час виконання домашнього завдання. Найбільш складне завдання перевіряється за розв’язком на екрані.

ІІІ. Актуалізація опорних знань і вмінь учнів.

Фронтальна бесіда:

1) Яка функція називається квадратичною?

2) Що є графіком квадратичної функції?

3) Як може бути розміщена парабола відносно осі абсцис?

4) Від чого це залежить?

5) Як впливає коефіцієнт а на напрям віток параболи?

6)Що відбувається з графіком квадратичної функції при зростанні коефіцієнта а?

7)Що таке нулі функції?

8) Охарактеризуйте графік функції y = x².

9) Розказати про послідовність побудови графіка квадратичної функції.

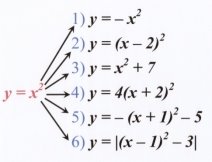$C:\Documents and Settings\Администратор\Мои документы\Мои рисунки\MP Navigator\2008_01_11\IMG_0003.jpg$ 10) Як із графіка функції y = x² одержати графіки наступних функцій:

11) Вказати координати вершин кожної з функцій а) – є).

12)Задати формулами функції, графіки яких зображені на малюнку:

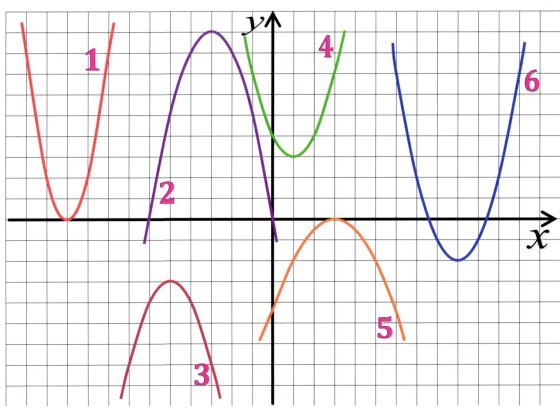
$C:\Documents and Settings\Администратор\Мои документы\Мои рисунки\MP Navigator\2008_01_11\IMG_0001.jpg$

13) Для яких із цих функцій виконується умова:

1) a> 0, D> 0;

2) a< 0, D> 0;

3) a> 0, D< 0;

4) a< 0, D = 0;

5) a< 0, D< 0?

ІV. Розв’язування вправ.

На дошці вивішуються формули функцій, графіки яких будуть будуватися на

протязі уроку.

Побудувати графік функції y = – x² – 8х – 12 за допомогою елементарних

перетворень графіка функції y = x².

Питання до класу:Що потрібно зробити, щоб можна було даний графік побудувати за допомогою елементарних перетворень графіка функції y = x²?

y = – x² – 8х – 12 = – (x²+ 8х + 12) = – ( x²+ 2 · 4х + 16 – 16 + 12) =– ((x + 4)²– 4) = – (x + 4)²+ 4.

(Поки один із учнів виконує вправу на дошці, троє учнів виконують аналогічну вправу на місцях:

y = x² – 8x + 7

y = 3x² – 12x + 9

y = 0,25x² – 3x + 8

Побудувати графік функції y = 3x² – 12х + 9.

Питання до класу:За яким алгоритмом будується графік квадратичної функції?

Знаходимо нулі функції:

3x² – 12х + 9 = 0;

x² – 4х + 3 = 0;

х₁ = 1; х₂ = 3.

Отже, графік даної функції перетинає вісь х в точках х₁ = 1; х₂ = 3.

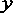
Знаходимо координати вершини параболи за формулами:
;

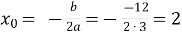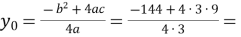
Отже, вершина параболи знаходиться у точці (2; – 3)

Знаходимо точку перетину з віссю y:

y(0) = 9. Отже, (0; 9) – точка перетину з віссю y.

(Поки один із учнів виконує вправу на дошці, двоє учнів виконують аналогічну вправу на місцях:

y = 3x² – 6x

y = – 2x²+ 8x – 6

y = – 0,5x² – 3x + 2,5

Побудувати графік функції y = |3x² – 12х + 9|

Питання до класу:Як із графіка функції y = f(x) одержати графік функціїy= |f(x)|?

Послідовність побудови: y = 3x² – 12х + 9y = |3x² – 12х + 9|

y = 3x² – 12х + 9y = |3x² – 12х + 9|

Побудувати графік функції y = 3x² – 12|х| + 9.

Питання до класу:Як із графіка функції y = f(x) одержати графік функціїy = f(|x|)?

Послідовність побудови: y = 3x² – 12х + 9y = 3x² – 12|х| + 9

y = 3x² – 12х + 9y = 3x² – 12|х| + 9

Скільки коренів має рівняння |3x² – 12х + 9| = mзалежно від параметра m?

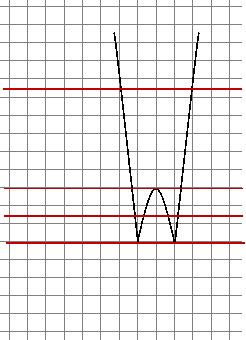
Щоб виконати це завдання, потрібно в одній системі координат побудувати графіки функцій y = |3x² – 12х + 9| та y = m для декількох характерних значень m, щоб визначити кількість спільних точок графіків функцій, що й буде вказувати на кількість коренів даного рівняння.

При m<0 рівняння коренів немає;

при m=0 рівняння має 2 корені;

при 0<m<3 рівняння має 4 корені;

при m= 3 рівняння має 3 корені;

при m> 3рівняння має 2 корені.

V. Застосування параболи.

Квадратична функція або її графік, парабола, дуже часто зустрічається в різноманітних галузях наукиі виробництва. Наприклад, у геометрії квадратичною функцією виражається залежність площі квадрата від його сторони, площі круга від його радіуса тощо. У фізиці – це, наприклад, залежність пройденого шляху від часу при прямолінійному рівноприскореному русі.

В астрономії парабола також зустрічається. Відомо, наприклад, що якщо космічному кораблю чи штучному супутнику, який обертається навколо Землі, надати другу космічну швидкість, то його траєкторія руху перетвориться з еліптичної в параболічну, і він зможе покинути Землю.

Інженерні розрахунки показують, що різні споруди, мости, арки у формі параболимають підвищену міцність.

Учень 1.Оптичні властивості параболічних дзеркал.

До наших днів дійшла легенда про те, як Архімед збудував увігнуті дзеркала і за їх допомогою спалив римські кораблі. Більшість вчених відкидають цю легенду, оскільки такі дзеркала повинні були би мати надто великі розміри, а при тодішньому розвитку техніки це було неможливо.

Але навіть якщо історія про спалення кораблів є легендою, то все ж таки спалити римський флот з допомогою параболічних дзеркал можливо.

Результати, які отримав Архімед, ґрунтувалися на такому твердженні: будь-яка пряма, паралельна осі симетрії параболи, після відбиття від параболи проходить через її фокус. Для того, щоб збудувати дзеркало, що збирає сонячні промені в одній точці, потрібно відшліфувати його по параболоїду обертання. Параболоїд – це поверхня, яку можна одержати, якщо обертати параболу навколо своєї осі.

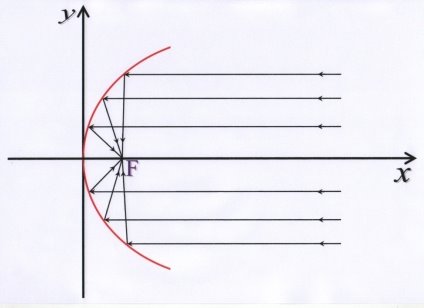$C:\Documents and Settings\Администратор\Мои документы\Мои рисунки\MP Navigator\2008_01_11\IMG_0001.jpg$ Якщо спрямувати таке параболічне дзеркало на Сонце, то всі відбиті промені пройдуть через фокус параболи, і температура в фокусі виявиться настільки великою, що з допомогою сонячних променів можна буде закип’ятити воду, розплавити свинець і інше. Звідси й походить назва ”фокус”, що на латині означає “вогнище”.

Учень 2.Парабола і військова справа.

Траєкторією руху снарядів цікавилися багато вчених, особливо з моменту винайдення пороху в ХІІІ столітті. Жодне укріплення не могло довго витримати артилерійську стрільбу. Пізніше здогадалися застосовувати навісну стрільбу, яка дозволяла стріляти із-за укриття.

Щоб забезпечити точне попадання, потрібно було вивчити рух тіла, кинутого під кутом до горизонту. Вчені довели, що таке тіло рухається по параболі.

Якщо при заданій початковій швидкості снаряда змінювати кут α, то одержуємо нескінченну кількість парабол. Всі параболи, для яких 45˚ <α< 90˚, дотикаються до одної і тої ж лінії, рівняння якої . Її називають параболою безпеки.

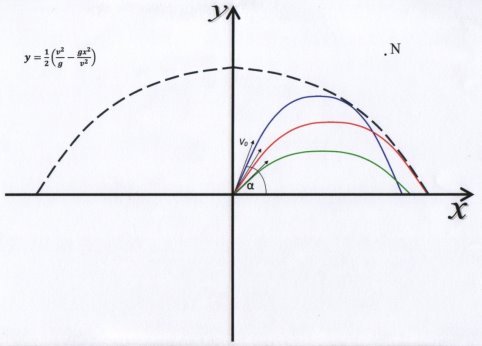$C:\Documents and Settings\Администратор\Мои документы\Мои рисунки\MP Navigator\2008_01_11\IMG_0001.jpg$ Якщо точка N знаходиться поза областю, що обмежується цією параболою, то при початковій швидкості vснаряд не потрапить у точку N при жодному куті нахилу.