Урок "Квадратична функція, її властивості та графік".

Підготувала

 Овсянникова Валентина Григорівна, вчитель Бутівського ліцею Чмирівської сільської ради, Луганська область.

Тема уроку:         Квадратична функція. ЇЇ властивості та графік.

Мета:       Повторити загальні властивості функцій, основні    геометричні перетворення графіків. Сформувати поняття квадратичної функції, вміння знаходити координати вершини та нулі функції, визначати напрям віток графіка, формувати первинні вміння будувати графік квадратичної функції за алгоритмом.

Розвивати критичне мислення, вміння аналізувати, порівнювати та робити висновки, комунікативні здібності.

Виховувати почуття прекрасного, графічну культуру, мовленєву культуру , наполегливість, інтерес до вивчення предмета.

Обладнання:   роздатковий матеріал ( доміНУШка, математична карусель, лото), ПК , мультимедійна дошка, презентація.

Тип уроку:    Формування знань, вироблення первинних умінь та навичок.

                                                 Хід уроку.

                                                    « Предмет математики настільки                                              серйозний, що не варто нехтувати нагодою зробити його трішечки              цікавішим.»                        

                                                                                Блез Паскаль

І. Організаційний етап.

 Учні поділено на три групи.

ІІ. Актуалізація опорних знань. ( 7 хв.)

1. Усна робота: а) що називають функцією;

   б) способи задання функції;

   в) які функції нами вже вивчено. 

     2)  Робота на місцях з роздатковим матеріалом.

        І група – « Математична карусель» - формули функцій.

        ІІ група – «ДоміНУШка» - « Продовжи речення».

        ІІІ група – « Властивості функцій».

2. Робота з дошкою – Learning Apps « Перетворення графіків функцій».

2575905(графіки елементарних функцій)

2576793 ( геометричні перетворення графіків функцій)

ІІІ. Мотивація навчальної діяльності. ( 3 хв.)

У навколишньому світі є багато предметів, що описують деяку математичнуфункцію.Володіння технікою побудови графіків часто допомагає розв’язати чимало завдань й інколи єдиним засобом розв’язання. Графік – мова математики.

Сьогодні ми поглибимо свої знання про квадратичну функцію.

Що є графіком квадратичної функції? (парабола)

По параболі летить і кинутий вами камінь, і м’яч.

Де зустрічаємо параболу у житті? Презентації учнів Перегуди І. та Войтенка А.

Практика та інженерні розрахунки показують, що різні споруди, мости, арки у формі параболи мають підвищену міцність. Є наука « опір матеріалів» - це наука про інженерні методи розрахунку на міцність, жорсткість і стійкість елементів конструкцій, машин і споруд.

ІV. Формування знань.

1. Означення квадратичної функції. 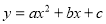, де .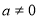

     Приклади  квадратичних функцій: y = ;

                                                                 y= ;

                                                                 y= .

2. Графік квадратичної функції.

Графіком квадратичної функції завжди є парабола, вітки якої напрямлені вгору при а>0 і вниз при а<0.

Координати вершин параболи: , , де .

Вісь симетрії параболи задана рівнянням: .

3.Алгоритм побудови графіка квадратичної функції .( Записано на дошці, одночасно працюємо в зошитах).

1. Обчислити координати вершини параболи.
2. Знайти координати точок перетину з осями координат:

а) з віссю абсцис: розв’яжемо рівняння .

Парабола може й не перетинати осі абсцис.

б) з віссю ординат: .

3. Позначити знайдені точки на координатній площині і з’єднати їх плавною лінією.

Але для більшої точності побудови параболи можна взяти додаткові точки, координати яких записуємо в таблицю.

Графіки квадратичних функцій , і можна побудувати, виконавши відповідні геометричні перетворення графіка функції .

 Робота в зошитах. Побудова графіка y = .

4. Властивості квадратичної функції ( усно проговорити з учнями).

Звернути увагу, що даний матеріал – параграф 11.

Якщо а>0 (вітки параболи напрямлені вгору), тоді

1. область визначення функції – уся множина дійсних чисел;
2. область значень – промінь ;
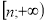3. якщо 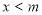, то функція спадає, при 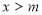– зростає;
4. якщо 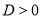, то функція має два нулі: 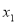і ;
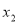5. на проміжку 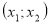значення функції від’ємні, на проміжках 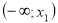і 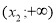– додатні.

Якщо а<0 (вітки параболи напрямлені вниз) і властивості 2), 3), 5) формулюються інакше (навпаки).

V. Осмислення матеріалу.

1) За підручником с. 114, № 442( а, б).

2) Робота з графіком ( рис.) – назвати координати вершини, напрям віток по знаку коефіцієнта а, точки перетину з віссю Ох та Оу, вісь симетрії.

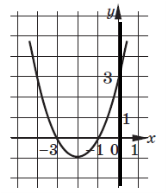
VІ. Рефлексія. Робота з хмаркою слів ( інтернет додаток Word clouds). Підсумок уроку.

VІІ. Домашнє завдання : вивчити параграф 11, розібрати усно приклад 1(с.110) , розв’язати:  с. 115, № 442(в, д),  445(а), 446(а).