Урок "Розв'язування цілих раціональних нерівностей . Метод інтервалів"

Урок алгебри 9 клас

 

Тема: «Розв'язування цілих раціональних нерівностей.

Метод інтервалів».

Тип уроку: Урок засвоєння нових знань.

Мета уроку: Сформувати поняття інтервалів знакосталості. Познайомити  учнів з методом інтервалів і побудувати на його основі алгоритм розв'язання цілої нерівності та сформувати  уміння його застосовувати.

Обладнання: Презентація.

Хід уроку

1. Мотивація учбової діяльності.

− Добрий день, діти! Що ми з вами навчились робити на останніх уроках?

( Розв'язувати нерівності другого степеня, за допомогою графічної схеми).

– Результати самостійної роботи показали, що ви добре навчились застосовувати алгоритм розв'язання таких нерівностей.

– Сьогодні ви продовжуєте вивчати тему «Раціональні нерівності». Ви розширите свої знання про види нерівностей та  способах їх розв'язання. А ваш досвід у роботі з раціональними рівняннями і  квадратними нерівностями  буде  опорою у вивченні нової теми. Не можна не погодитися з висловлюванням давньогрецького ученого Анаксагора (бл. 500-428 до н. е.) (Слайд 1)

 «Жодна річ не виникає, не знищується, але кожна складається зі змішування існуючих речей або виділяється з них».

У цьому ви переконаєтесь вже сьогодні на уроці.

– Що нам на уроках буде допомагати у «здобуванні» нових математичних знань? (Відповіді учнів)

– Бажаю успішної праці!

2. Актуалізація опорних знань.

− На попередніх уроках ви отримали означення раціональних і цілих алгебраїчних виразів:  (Слайд 2)

Означення.

 

 Вирази, складені зі змінних величин і чисел за допомогою арифметичних операцій, називають раціональними виразами алгебри.

 

 

Означення.

 Раціональні вирази, що не містять змінної у знаменнику, називають цілими раціональними виразами.

 

Сформулюйте означення цілої раціональної нерівності.

Означення 1. (Слайд 3)

 Раціональною нерівністю називається нерівність, обидві частини якої є раціональними виразами.

 

Означення 2.

 Цілою нерівністю називається раціональна нерівність, обидві частини якої є цілими виразами.

 

–Давайте згадаємо, як ми розв'язували квадратичні нерівності на попередньому уроці.

 

Виконайте № 1. Розв'яжіть нерівність  х² – 4х –12  0 (Слайд 4)

 

Можливий варіант відповіді:

№ 1.  

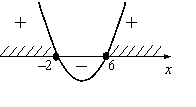   х² – 4х –12  0

  х² – 4х –12 = 0

  х_{1 =} -2, х₂= 6

 

 

 

а) При x ∈ (–2; 6) квадратний тричлен х² – 4х –12 має знак «–»,

а при x ∈ (–∞; –2) ⋃ (6; +∞) – знак «+».

б) Корені тричлена х² – 4х –12 розбивають числову пряму на три інтервала:

 (–∞; –2), (–2; 6), (6; +∞).

в) Функція у = х² – 4х –12 на кожному з цих інтервалів змінює свій знак. Такі інтервали называються інтервалами (проміжками) знакосталості.

3. Постановка проблеми

− Настав час виконати пробне завдання. (Слайд 5)

– Як можна назвати нерівність (х – 1)(х – 2)(х – 3)²(х – 4) > 0? (раціональною, цілою)

№ 2.  Розв'яжіть нерівність:

(х – 1)(х – 2)(х – 3)²(х – 4) > 0

 Учні  самостійно намагаються виконати завдання. Час на виконання завдання обмежено.

– Обговоріть у групах, які труднощі можуть виникати?

 Учні висловлюють свої думки, або відповідають що не можуть знайти відповідь, або не можуть відповідь обґрунтувати, найкращій з варіантів, якщо  діти запропонують  об'єднання систем, але дадуть обґрунтування що такий шлях занадто  не раціональний і довготривалий. Приходять до висновку, що не знають алгоритм розв'язання такої нерівності.

 Потрібно було вирішити цілу нерівність. Ми знаємо способи розв'язання лінійної та квадратної нерівностей. Труднощі виникли при вирішенні цілої нерівності, яка не є ні лінійною, ні квадратною. Причина в тому, що ми не знаємо способу розв'язання цілих нерівностей.

• Що ви пропонуєте?

–   Складіть у групах план ваших дій.

Учні працюють у групах, складають план дій.

Можливий варіант відповіді:

1. Виконати завдання, запропоновані вчителем, проаналізувати хід виконання, результати.

2. Сформулювати гіпотезу.

3. Порівняти з методом, запропонованим у підручнику. 

– Сформулюйте тему уроку (Слайд 6)

Розв'язування цілих раціональних нерівностей.

Метод інтервалів

4. Вивчення нового матеріалу.

Учитель пропонує виконати наступні завдання

– Виконайте №3. Використовуючи результати виконання попереднього завдання доповніть схему і поясніть знаки добутку (х – 6)(х + 2). (Слайд 7)

 

 

 

 

 

 

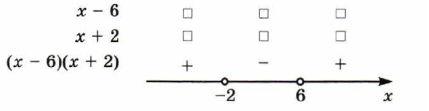
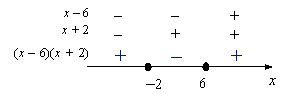
 Знак добутку додатній, якщо обидва множники мають однаковий знак; знак добутку – від’ємний, якщо множники мають різні знаки.

 Щоб знайти інтервали знакосталості, треба:

 1) знайти ті значення х, при яких множник дорівнює нулю, тобто його корінь;

 2) позначити їх на числовій прямій;

 3) встановити знак кожного множника на кожному з інтервалів, що утворилися, і знайти знак добутку (х – а)(х – b) за відомим правилом.

№ 4. Яка з нерівностей не є рівносильною іншим? (Слайд 8)

 

а) 3х² – 10х + 3 < 0;  в) –3х² + 10х – 3 < 0;

б) (х – 3)(3х – 1) < 0;  г) 3(х – 3) < 0.

Нерівність –3х² + 10х – 3 < 0 не є рівносильною іншим, так як

 

–3х² + 10х – 3 < 0 ⇔ 3х² – 10х + 3 > 0.

А нерівності 3х² – 10х + 3 < 0 ⇔3(х – 3) < 0 ⇔ (х – 3)(3х – 1) < 0

(3 і корені квадратного тричлена 3х² – 10х + 3).

 

Як ще можна розв'язати цю нерівність?

 

 Нерівність  х² – 4х –12  0 можна тепер розв’язати, не використовуючи графік квадратичної функції:

1) знайти корені квадратного тричлена та розкласти його на множники;

2) позначити корені на числовій прямій;

3) встановити знак кожного множника та знайти знак добутку (х – а)(х – b) на кожному з утворених інтервалів,

4) вибрати ті числові проміжки, які задовольняють цій нерівності.

 

Цей спосіб не підійде для розв'язання  квадратних нерівностей, якщо вони не мають коренів.

 

5.Засвоєння нового матеріалу.

Метод інтервалів включає наступні кроки:  (Слайд 9)

 

1. Виділити на числовій осі х інтервали знакосталості.

2. Визначити знак виразу  на кожному з інтервалів.

3. Вибрати інтервали, які відповідають знаку нерівності.

4. Якщо нерівність нестрога, включити у відповідь кінці інтервалів.

 

№ 5. Розв'яжіть методом інтервалів нерівність (х – 1)²(х – 2)³ > 0

 

 

 

 

 

1) Знак (х – 2)³ при переході через точку 2 змінюється, а знак (х – 1)²  при переході через точку 1 не змінюється?

При переході через точку знак двочлена (х – а)ⁿ не змінюється, якщо показник n парний і – змінюється, якщо показник n непарний.

6) Розв'яжіть методом інтервалів нерівність (х – 1)(х – 2)(х – 3) (х – 4) > 0.

 

 

 

 

 

 

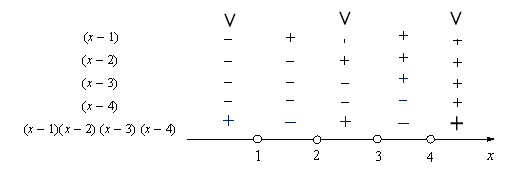
Правило зміни знаків добутку множників вида (х – а)ⁿ (Слайд 10)

 

 При переході через точку а знак добутку

• не змінюється, якщо множник (х – а) має парний показник степеня;
• змінюється на протилежний, якщо множник (х – а) має  непарний показник степеня.

№ 6. Розв'яжіть методом інтервалів нерівність: – х (3х⁴ + 2х + 5) < 2 – 3х⁵. (Слайд 11)

 

 

а) 1) Перетворимо нерівність, розкривши дужки в лівій частині, перенісши доданки з правої частини в ліву, звівши подібні доданки та розділивши обидві частини нерівності на (– 1) :

– х (3х⁴ + 2х + 5) < 2 – 3х⁵

– 3х⁵ – 2x² – 5x + 3х⁵ – 2 < 0

– 2x² – 5x – 2 < 0

2x² + 5x + 2 > 0

2) Знайдемо корені квадратного тричлена 2x2 + 5x + 2  і розкладемо його на множники:

2x² + 5x + 2 = 0 ⇔ 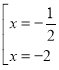                             2x² + 5x + 2 = 2

Таким чином, початкова нерівність звелася до розв’язання нерівності виду:

2 > 0

 

3) Використовуємо  метод інтервалів.

 

 

 

 

 Зазначимо знайдені корені на координатній прямій. Поставимо знаки добутку справа наліво, починаючи із знака «+», у порядку чергування (немає жодного множника в парному степені). Виділимо ті інтервали, які відповідають нерівності.

4) Запишемо відповідь: (–∞; –2) ⋃ (–0,5; +∞).

– Повертаємось до пробного завдання:  (Слайд12)

 

 (х – 1)(х – 2)(х – 3)²(х – 4) > 0.

 

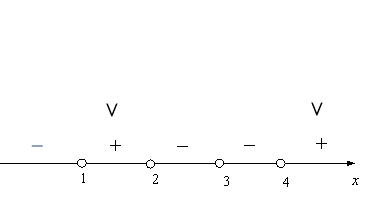(х – 1)(х – 2)(х – 3)²(х – 4) = 0 ⇔

 

 

 

 

Відповідь: х ∈ (1; 2) ⋃ (4; +∞).

6. Закріплення.   (Слайд 13)

№1.    

(х – 1)³(х + 2)²(х – 3) = 0 ⇔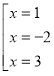

 

 

 

 

Відповідь: х ∈ (–∞; –2) ⋃ (–2; 1) ⋃ (3; +∞).

№2.

(х + 10)(х + 9)²(х + 8)⁴ = 0 ⇔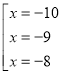

 

 

 

 

 

 

Відповідь: х ∈ [–10; +∞).

7.Самостійна робота з самоперевіркою за зразком:   (Слайд 14)

Розв’яжіть нерівність  методом інтервалів:.

 

зразок

(х – 1)(х + 2) = 0 ⇔               Відповідь: х ∈ [–2; 1].

8. Рефлексія діяльності на уроці. (Слайд 15)

9. Домашнє завдання.