Урок "Логарифмічна функція та її властивості "
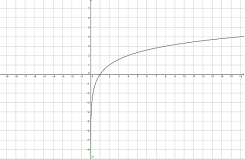
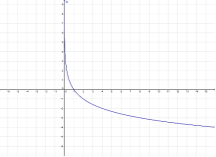
Логарифмічна функція, її графік і властивості
Мета:
- ввести поняття логарифмічної функції;
- формувати вміння будувати графік логарифмічної функції, дослідити її властивості;
- розвивати пізнавальний інтерес, творче мислення учнів, математичне мовлення;
- виховувати волю та наполегливість у досягненні кінцевого результату;
- ознайомити учнів з використанням логарифмічної функції при вивченні явищ навколишнього світу, показати міжпредметні зв'язки.
Тип уроку: урок засвоєння нових знань, умінь.
Обладнання: підручники «Алгебра 11клас» А. Г. Мерзляк та ін., «Математика 11 клас» Г. П. Бевз, В. Г. Бевз, комп’ютерна презентація «Логарифмічна функція, її графік і властивості», бланки для заповнення «Властивості логарифмічної функції», картки з індивідуальними завданнями
Хід уроку
- Організаційний момент
Учитель.
- Доброго дня! Сідайте. Розпочинаємо наш урок.
Налаштування учнів на позитивний лад.
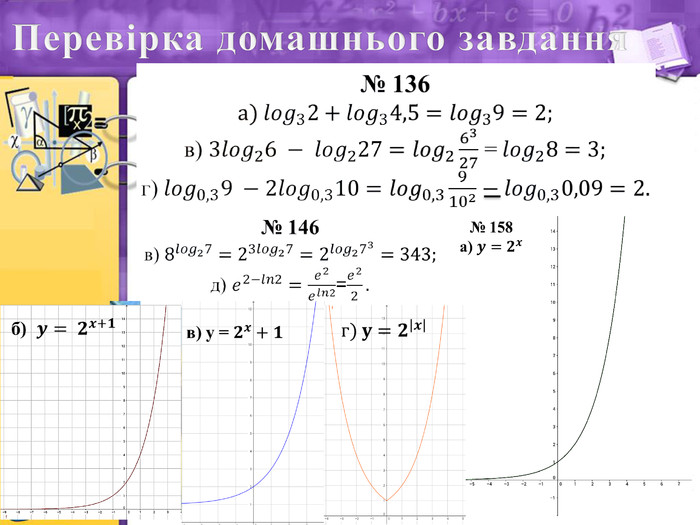
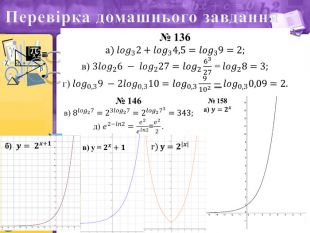
- Перевірка домашнього завдання
Учитель.
- На попередніх уроках ви ознайомилися з поняттям «Логарифми та їх властивості» На сьогодні ви мали виконати № 136(а,в,г), 146(в,д), 158.
- У чому полягали труднощі під час виконання даних завдань?
- Правильність виконання завдання ми звіримо із розв’язанням на дошці.
- Якщо перший приклад правильно, то відкриваємо його і таким чином перевіряємо решту прикладів, відкриваючи картинки – вставки, поки не з’являться нові зображення.
- Мотивація навчання
Учитель.
- Що на Вашу думку об’єднує ці малюнки?
-
 Чому вони присутні у нас на уроці?
Чому вони присутні у нас на уроці?
- Як їх можна пов’язати з темами, що ми вивчаємо, і з математикою взагалі?
- Відповіді на ці запитання ми отримаємо під час уроку.
- Темою нашого уроку є «Логарифмічна функція, її графік і властивості ». (учні в зошитах записують дату, тему)
- Метою нашого уроку є…
(Учитель формулює мету уроку)
- Для досягнення мети пройдемо такі етапи уроку…
- Гра «Незакінчене речення» (Актуалізація опорних знань учнів)
Учитель.
- Повторення теоретичного матеріалу проведемо у вигляді гри «Незакінчене речення».
- Отож закінчіть речення
- Залежність змінної y від змінної x, при якій кожному значенню x відповідає єдине значення y називають функцією
- Множина значень, яких набуває незалежна змінна (аргумент) називають областю визначення функції
- Множину значень, яких набуває залежна змінна (функція) називають областю значень функції
- Значення аргументу, при яких значення функції дорівнюють нулю, називають нулями функції
- Функцію називають спадною на деякому проміжку, якщо кожному більшому значенню аргументу з цього проміжку відповідає менше значення функції
- Функцію називають зростаючою на деякому проміжку, якщо кожному більшому значенню аргументу з цього проміжку відповідає більше значення функції
- Графіки взаємно обернених функцій симетричні відносно прямої y = x
- Вивчення нового матеріалу
Учитель.
-
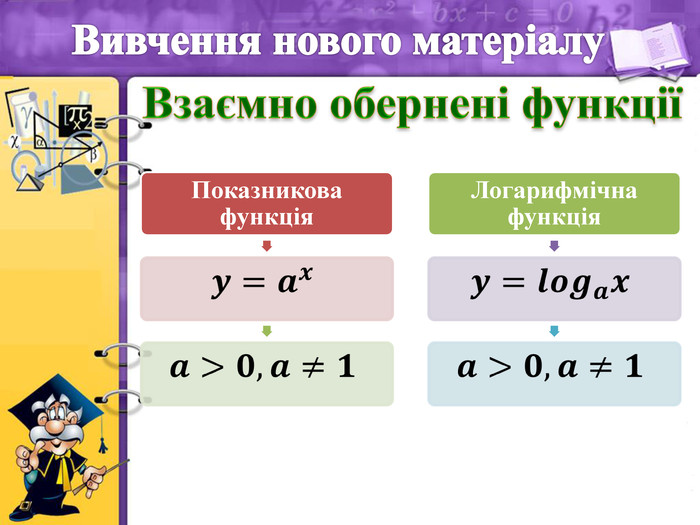
На попередніх уроках ми вивчали функцію
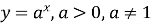 , яка називається …? (показниковою)
, яка називається …? (показниковою)
- Оскільки ця функція є монотонною, тому вона має обернену функцію. Задамо обернену функцію формулою. Що для цього необхідно зробити?
-
1) З формули
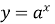 виразимо змінну
виразимо змінну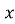 через
через 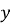 :
: 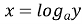 ;
;
-
2) змінимо позначення змінних, одержимо формулу
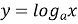 якою й задається обернена функція.
якою й задається обернена функція.
-
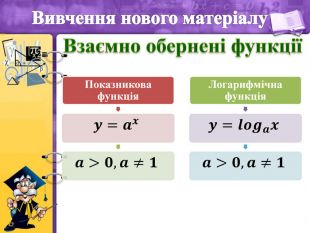
Функція виду
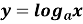 ,
, 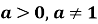 називається логарифмічною функцією.
називається логарифмічною функцією.
- Для побудови графіка логарифмічної функції та формулювання її властивостей, я пропоную вам виконати такі завдання в групах:
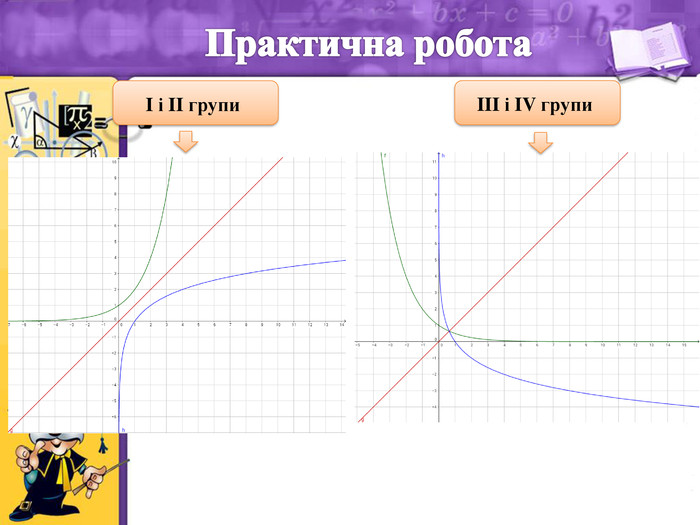
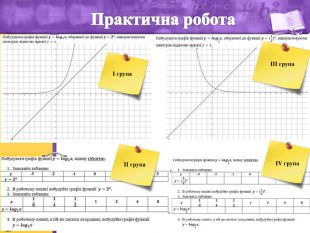
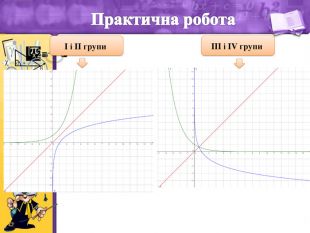
- Практична робота
Учитель. У кожного із Вас на партах є картки із завданнями для практичної роботи із коротким описом виконання завдання.
Учитель. Графік функції ![]() , можна отримати з графіка функції
, можна отримати з графіка функції ![]() симетричним відображенням відносно прямої
симетричним відображенням відносно прямої ![]()
I група. Побудувати графік функції ![]() , оберненої до функції
, оберненої до функції ![]() ,
,
використовуючи симетрію відносно прямої ![]() .
.
II група. Побудувати графік функції ![]() , задану таблично.
, задану таблично.
III група. Побудувати графік функції ![]() , оберненої до функції
, оберненої до функції ![]() ,
,
використовуючи симетрію відносно прямої ![]() .
.
IV група. Побудувати графік функції ![]() , задану таблично.
, задану таблично.
(Учні працюють в парах, будуючи графіки логарифмічної функції різними способами. Виконавши побудови графіків, вони мають можливість порівняти, чи однакові в них графіки.)
Учитель. Результати Вашої роботи звірте із дошкою.
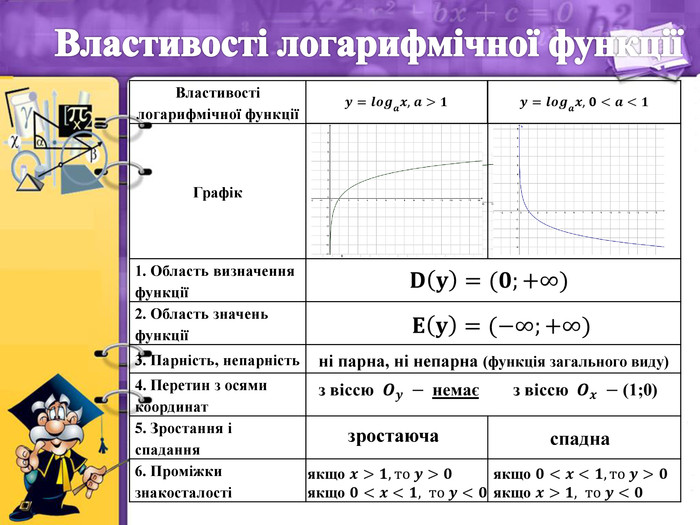
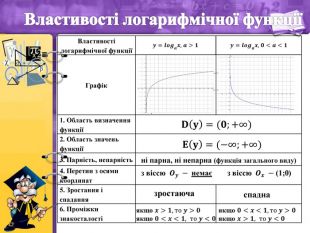
- Властивості логарифмічної функції
Учитель. У Вас на партах лежать бланки «Властивості логарифмічної функції». На основі раніше вивчених властивостей показникової функції і отриманих графіків логарифмічної функції встановимо її властивості. Відповіді записуйте у бланк.
Система запитань:
- Областю визначення логарифмічної функції є проміжок …Чому? (для показникової функції – це область значень);
- Областю значень є…
-
Нулі функції…(
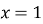 )
)
- Проміжки зростання і спадання…
- Проміжки знакосталості…(проміжки визначаємо за графіком)
Бланк «Властивості логарифмічної функції»
|
Властивості логарифмічної функції |
|
|
|
Графік |
|
|
|
1. Область визначення функції |
|
|
|
2. Область значень функції |
|
|
|
3. Парність, непарність |
|
|
|
4. Перетин з осями координат |
|
|
|
5. Зростання і спадання |
|
|
|
6. Проміжки знакосталості |
|
|
- Історична довідка
Учитель. Винахід логарифма пов’язаний із двома постатями: швейцарцем Йостом Бюргі (1552—1632), знаним годинникарем і майстром астрономічних інструментів, і шотландцем Джоном Непером (1550—1617), який теж не був математиком за професією, астрономія була його «хобі». А Бюргі працював разом з астрономом Іоганном Кеплером.
Саме величезний обсяг необхідних в астрономії обчислень і спонукав Бюргі і Непера шукати шляхи для їх спрощення. 20 років присвятив Непер своїм логарифмічним таблицям, аби, за його словами, «позбутися нудних і складних обчислень, які відлякують зазвичай багатьох від вивчення математики». Обидва автори прийшли до своїх таблиць незалежно один від одного. Вони склали таблиці так званих натуральних логарифмів. Бюргі працював над таблицями 8 років і видав їх у 1620 році під назвою «Арифметична і геометрична таблиця прогресії». Проте його таблиці не набули широкого поширення, бо Непер видав свій «Опис дивовижної таблиці логарифмів» на 6 років раніше. Тому і визнали число «е» неперовим числом.
Упродовж майже трьох із половиною сторіч відтоді, як у 1614 році були опубліковані Непером перші логарифмічні таблиці, вони служили астрономам і геодезистам, інженерам і морякам, скорочуючи час на обчислення і, як сказав французький учений Лаплас, продовжуючи життя обчислювачам.
Учитель. Логарифмічна спіраль – особливий вид спіралі, що часто трапляється в природі.
Характерні особливості логарифмічної спіралі:
- Має нескінченну кількість витків як при розкручуванні так і при скручуванні, її називають рівнокутною спіраллю;
- у будь-якій точці спіралі кут між дотичною до неї та її радіус-вектором зберігає постійне значення;
- при різних перетвореннях (гомотетії, повороті) вона залишається незмінною.
- має широке застосування в технічних приладах;
- властивості цієї кривої так вразили Якоба Бернуллі, що він назвав її spira mirabilis (чудова спіраль) і заповів зобразити її на його могилі з написом (перетворювана, відроджуюся знову).
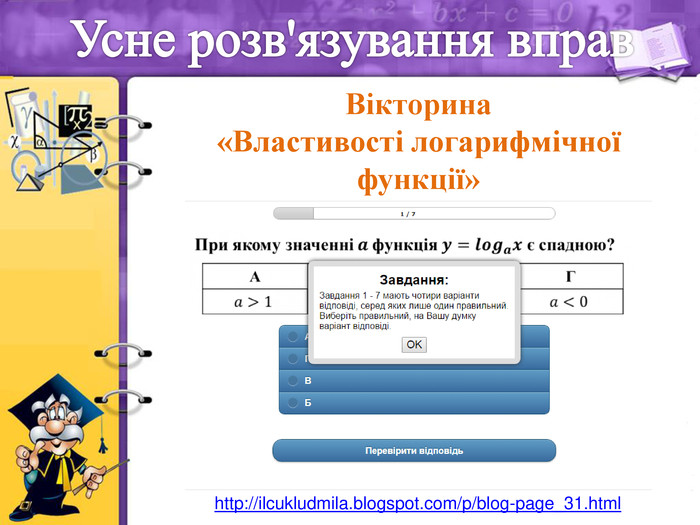
- Усне розв’язування вправ
Учитель. Усне розв’язування вправ проведемо у вигляді вікторини.






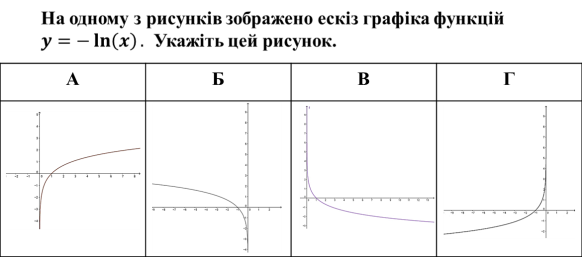
- Розв’язування задач з повним поясненням (з підручника)
Учитель. Виконаємо вправи з підручника №140, 142 (в, г), 152 (а, б, в, г), 153.
- Хто працює швидше, пропоную Вам наступні завдання.
№1
Знайдіть область визначення функції:
-
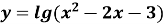 (
(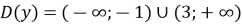 )
)
-
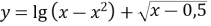 (
(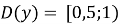 )
)
№2
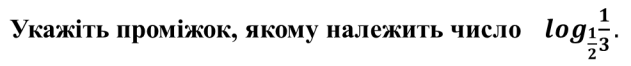
|
А |
Б |
В |
Г |
Д |
|
(-2;-1) |
(-1;0) |
|
(1;2) |
(2;3) |
![]()
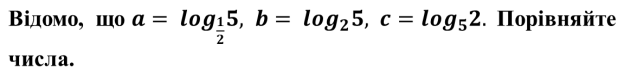
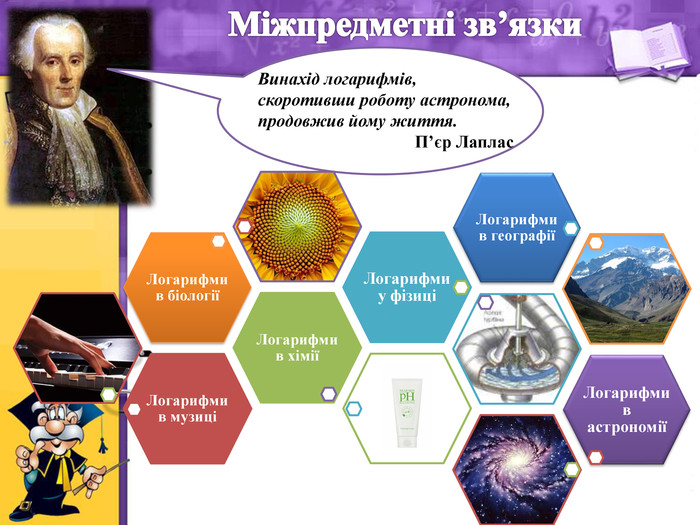
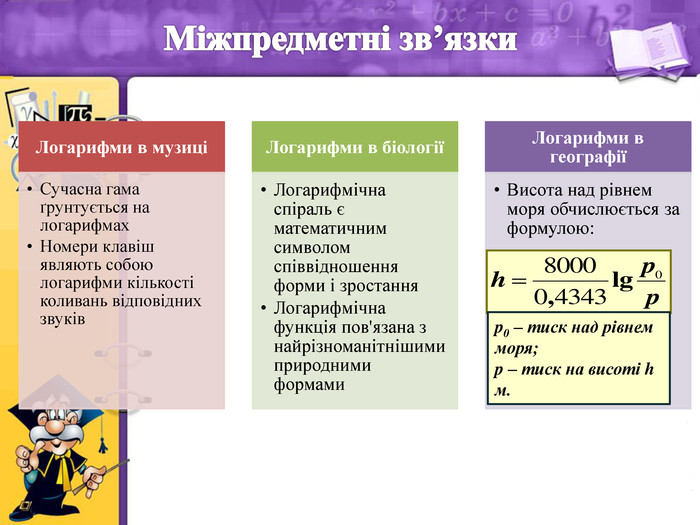
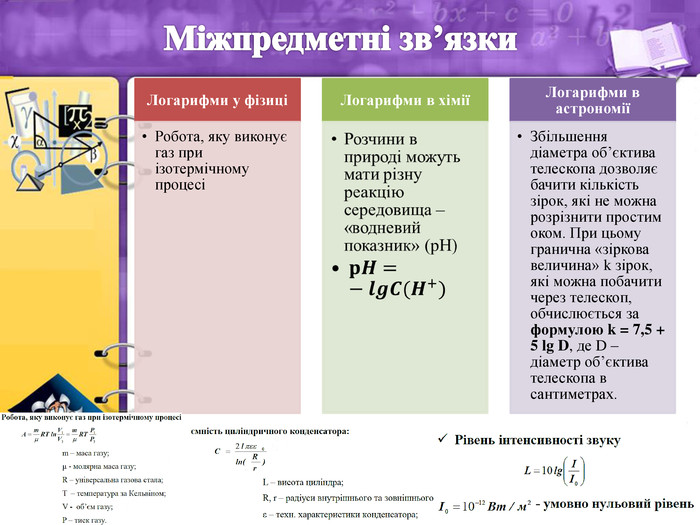
- Розв’язування задач практичного змісту (міжпредметні зв’язки)
Учитель. Різноманітне застосування логарифмів і логарифмічної функції пропоную Вам на наступних слайдах.
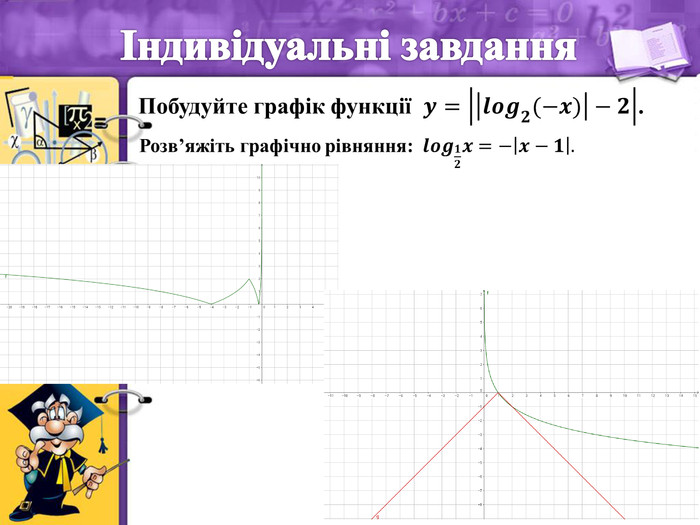
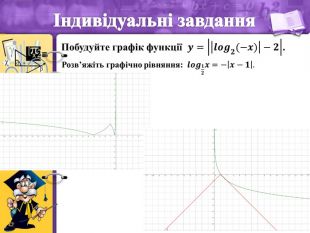
- Індивідуальні завдання
-
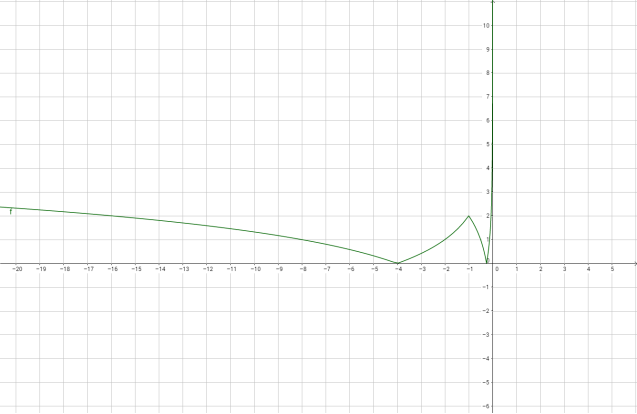
Побудуйте графік функції
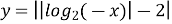 .
.
-
Розв’яжіть графічно рівняння:
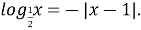
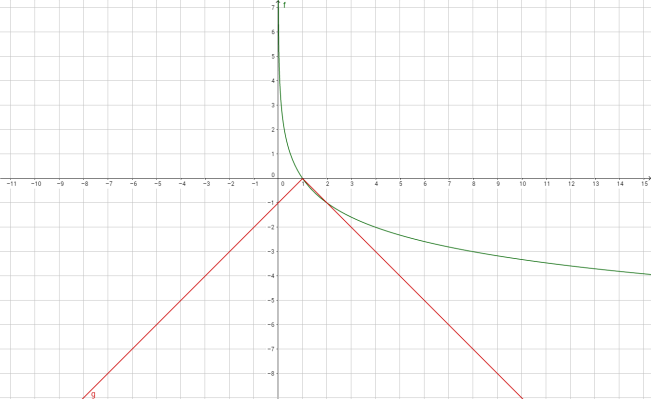
- Самостійна робота із взаємоперевіркою
Варіант 1

Варіант 2

Учитель. Ви перевірили результати своєї роботи. Які завдання викликали найбільші труднощі?
- Домашнє завдання
Вивчити § 4 (п.2).
Розв’язати № 154, 157(в, г, д).
Підготувати проект, вибравши одну із тем
- Оцінювання учнів
Учитель оцінює учнів за роботу біля дошки, за самостійне розв’язування учнів і за самостійну роботу.
- Підсумки уроку.
Учитель. Сьогодні на уроці ми з Вами ввели поняття логарифмічної функції, навчилися різними способами задавати її графік, встановили її властивості і застосували їх до розв’язування різноманітних вправ.
Отже,
- Яка функція називається логарифмічною?
- Коли логарифмічна функція буде зростаючою (спадною)?
- Де використовується монотонність? (для порівняння)
- Областю визначення логарифмічної функції є…
- Де застосовується логарифмічна функція?
1


про публікацію авторської розробки
Додати розробку