Урок з алгебри для 11 класу на тему: "Показникові рівняння"

Про матеріал

Розробка уроку підготована з метою ознайомлення учнів з найпростішими показниковими рівняннями. (Повторити властивості степеня з дійсним показником. Вчити розв’язувати найпростіші показникових рівнянь)

Перегляд файлу

$D:\картинки математика\images (2).jpg$ Конспект уроку з алгебри для 11 класу на тему :

«Показникові рівняння».

Підготувала: учитель математики загальноосвітньої школи І-ІІІ ступенів №1 Охтирської міської ради Сумської області Пасішна Ольга Миколаївна

м. Охтирка

Учень повинен знати: методи розв’язування показникових рівнянь.

Предметні вміння та навички :

Розв’язування найпростіших тригонометричних рівнянь;
Застосування вміння розкладання многочленів на множники;
Введення нової змінної;
Застосування властивостей функцій;
Застосування графічного способу розв’язування рівнянь;
Розв’язування рівнянь, що містять змінну під знаком модуля;
Розв’язування рівнянь з параметром

Розв’язування найпростіших показникових рівнянь

$D:\картинки математика\images.jpg$ Ключові компетентності: спілкування державною мовою, вміти ставити питання, розпізнавати проблему, міркувати. Робити висновки на основі інформації, поданої в різних формах, грамотно висловлюватись, доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно, зрозуміло формулювати думку, аргументувати, доводити правильність тверджень. Усвідомлювати важливість математики як універсальної мови науки, техніки та технологій.

$D:\картинки математика\Без названия (1).jpg$

Девіз уроку:

Математика не лише вчить мислити,

а й уселяє віру у безмежні сили людського розуму.

Вона виховує волю, характер.

В.Сухомлинський

Хід уроку

$D:\картинки математика\1.jpg$ І. Актуалізація знань учнів:

- степінь з дійсним показником та його властивості;

- рівняння, розв’язування рівняння;

- показникові функція та її властивості;

- метод від супротивного для доведення теорем;

ІІ. Виклад нового матеріалу.

Показниковим називають рівняння, в якому змінна міститься в показнику степеня
Теорема 1. При 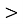а0, а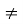1 рівність 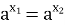виконується тоді і тільки тоді, коли х₁=х₂ .
Теорему доводимо, використовуючи властивості показникової функції та метод від супротивного.
Наслідок: 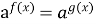виконується при f(x)=g(x)

ІІІ. Розв’язування найпростіших показникових рівнянь

Рівняння виду 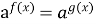при а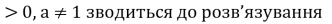 раціонального рівняння f(x)=g(x)

Завдання: розв’язати рівняння:

№	Умова	Вказівка
1	2^х=128	Представити 128 як степінь числа 2
2	3^5х+1=3^2х	Використати теорему (1)
3	=1	Використати властивість степеня з показником 0.
4		Представити 4 і 8 як степені з однаковою основою.
5	(3/2)^1-2х=(8/27)^х+3	Застосувати властивості степеня з від’ємним показником
6	(10^х-5)^х-6=100	Застосувати властивості степеня (піднесення степеня до степеня) і записати 100 як степінь числа 10.
7	(4/5)^х(35/12)^х=9/4	Застосувати властивості степеня (добуток степенів з спільним показником)
8		Врахувати, що степені з різними основами і однаковим показником рівні , якщо їх спільний показник дорівнює 0
9	4^х5^х-1=0,220^3-2х	Виконати дії в обох частинах рівняння
10	=	Записати вирази в лівій і правій частинах рівняння як степені з однаковою основою

IV. Закріплення знань учнів.

Виконати тестове завдання (10 балів). Розв’язати рівняння. вибрати правильну відповідь

№	Умова завдання
1	7^5х+6=49; А)-2; Б)-1: В)-0,8; Г)1; Д)5
2	2^3х4^х=2¹⁰; А)-2; Б)5; В)1; Г)0,2; Д)2
3	(1/2)^х(16/27)^х=(3/2)³; А)1; Б)0,1; В)-1; Г)2; Д)1,5
4	Знайти суму коренів рівняння: ; А)9; Б)3; В)-3; Г)2; Д)14
5	Визначте проміжок, в якому містяться корені рівняння: =4^х *0,25; А)[-2;-1); Б)[-1;0);В)[0;1);Г)[1;2);Д)[2;)

V. Підсумок уроку.

Які рівняння називають показниковими? Методи розв’язування найпростіших показникових рівнянь. Властивості степеня з дійсним показником.

VІ. Домашнє завдання.

1. Повторити : властивості степеня з дійсним показником; показникова функція і її властивості; розв’язування квадратних рівнянь; розкладання многочлена на множники

2. Розв’язати рівняння. Вказати способи розв’язування, основні властивості і теореми: