Урок "Математичне моделювання"

Додаток 2.

Тема: «Математичне моделювання».

Мета: Ввести поняття математичного моделювання; розглянути загальну задачу математичного моделювання, проілюструвати її прикладами; розвивати логічне мислення, інтерес до вивчення математики.

Тип уроку: урок засвоєння нових знань.

Обладнання: картки для роботи в групах, вислови про математику, моделі геометричних тіл, малюнки, схеми.

     Ми з насолодою пізнаємо математику…

                                                                 Вона захоплює нас, наче квітка лотоса.

 Аристотель

Хід уроку

1. Перевірка домашнього завдання.

2. Мотивація навчальної діяльності.

Учитель. Математика здавна має репутацію найточнішої галузі і є надійним знаряддям для розкриття таємниць природи. Близько 1800 р. до н.е. давньоєгипетський писар Ахмес переписав з більш раннього рукопису присвячений математиці папірус. Він починався красномовною обіцянкою навчити «досконалого і ґрунтовного дослідження всіх речей, розуміння їхньої суті, пізнання всіх таємниць…». Через три тисячоліття ту саму думку повторив індійський математик Бхаскара II (1114-1185): «Я глибоко шаную математику, бо ті, хто ознайомлений з нею, убачають у ній засіб до розуміння всього існуючого».

Зрозуміло, що можливості математики тих часів були обмеженими. У папірусі Ахмеса, наприклад, розкривалися лише таємниці лічби, обчислень дробами виду і алгоритмів розв’язання задач , які не виходять за межі сучасної дев’ятирічної школи. Але вже тоді математика виявила риси, характерні для всієї її багатовікової історії. Якась нестримна сила штовхала перших «колумбів математики» розв’язувати задачі, досягати точності обчислень, яка набагато перевищувала потреби практики. Людина формувала математичні поняття, створювала цілі теорії, щоб розв’язувати конкретні практичні задачі.

Математика пройшла довгий і складний шлях, перед тим як стати могутньою, надзвичайно розгалуженою галуззю теоретичних знань.

Як же математики, оперуючи абстрактними поняттями, можуть так ефективно вивчати глибинні закономірності навколишньої дійсності? Математики справді не вивчають живі організми, тверді тіла, рідини, гази, елементарні частинки, планети або галактики. Вони створюють математичні моделі досліджуваних об’єктів і відношень між ними. Наприклад, геометрія Евкліда, яку вивчають в школі, є математичною моделлю навколишнього тривимірного простору. Реальним об’єктом простору зіставляються математичні абстракції, які відображають певні властивості реальних фізичних об’єктів, - точки, відрізки, прямі й інші плоскі та просторові геометричні фігури.

3. Вивчення нового матеріалу.

1. Математична модель.

Учитель. Повернемося до задачі з домашнього завдання:

• про які поняття йдеться в задачі? (нематематичні поняття – книга, сторінки.)
•    яким методом розв’язували цю задачу? (математичним, використавши формулу суми членів арифметичної прогресії.)
•    чи існують у навколишньому світі математичні об’єкти? (Реально не існують усі вони створені людським розумом у процесі історичного розвитку людини та існують лише в уяві й у таких знаках і символах, які утворюють математичну мову.)

Об’єкт – це те, що є предметом розгляду (вивчення, впливу).  Математичні об’єкти – це ідеальні об’єкти, які відображають (описують) реальні об’єкти.

Задачі поділяють на математичні та прикладні.

Математичні задачі – це задачі, в яких об’єктами є математичні об’єкти (фігури, числа). Прикладні задачі – це задачі, умови яких містять нематематичні поняття. (Або це задачі, в яких об’єктам є реально існуючі об’єкти.)

(Пропонуємо учням придумати дві задачі: математичну та прикладну. У кожній з них треба назвати об’єкти, що розглядаються.)

Розв’язуючи прикладну задачу математичними методами, спочатку створюють її математичну модель.

Із поняттям «модель» (modele – зразок. копія) ви зустрічалися, розглядаючи моделі літака, автомобіля, піраміди, кулі тощо. Основна властивість кожної моделі полягає в тому, що вона відображає найсуттєвіші властивості оригіналу. Математична модель – це опис якогось реального об’єкта або процесу мовою математичних понять, формул, рівнянь тощо, що є записами законів природи, які керують досліджуваним об’єктом чи явищем.

2. Історична довідка.

Учень. Існує ціла наука – прикладна математика. Їй уже кілька тисячоліть. Учені стародавнього Єгипту обчислювали площі полів, об’єми приміщень тощо, уся математика тоді була прикладною.

У V-IV ст. до н.е. в Греції почала створюватися теоретична (чиста) математика.

Значний вклад у розвиток прикладної математики вніс український математик Михайло Кравчук – академік всеукраїнської академії наук, її вчений секретар, якого у 1938 році безпідставно репресували й засадили на Колиму, де він і загинув. (Демонструється портрет М. Кравчука.)

3. Приклади математичних моделей.

Задача 1. Скільки дошок потрібно, щоб настелити підлогу в кімнаті довжиною 9 м і шириною 5 м, якщо довжина дошки 6м а ширина 0,25 м?

Обговорення умови

1. Дана задача є математичною чи прикладною?
2. Назвіть об’єкти даної задачі. Вони математичні чи реальні?
3. Переформулюйте прикладну задачу в геометричну і розв’яжіть її. Що для цього потрібно зробити? Накресліть геометричну модель до задачі.

Розв’язання

Поверхня підлоги кімнати має форму прямокутника. Знайдемо його оскільки дошка площу:S_k=9×5=45 (м²).

Оскільки дошка також має форму прямокутника, то її площа: S_д=6×0,25=1,5 (м²).

Кількість дошок х дорівнює: х=45:1,5=30.

Відповідь. Зо дошок.

Задача 2. Із пункту а в пункт В виїхав велосипедист і рухався зі швидкістю 20 км/год., а через півгодини слідом за ним виїхав мотоцикліст і рухався із швидкістю 36 км/год. Через який час після виїзду велосипедиста його наздожене мотоцикліст?

Розв’язання

Можна побудувати різні математичні моделі до цієї задачі. Побудуємо математичну модель за допомогою графіків. Залежність шляху, пройденого велосипедистом, від часу можна задана формулою S₁=20t, а шляху, пройденого мотоциклістом, - формулою S₂=36(t-0.5). Щоб дати відповідь на запитання задачі, потрібно знайти абсцису точки А перетину графіків.

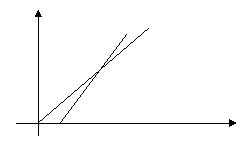
З малюнка знаходимо, що t=1,1 год.

Відповідь. t=1,1 год.

(Учні розв’язуючи задачі, доходять висновку, що реальне явище, описане в задачі, ми замінюємо ідеалізованим явищем – геометричною задачею; у цьому випадку розв’язок є наближеним. Математичне розв’язання будь-якої прикладної задачі завжди є наближеним.)

Учитель. Розв’язування будь-якої прикладної задачі математичними методами здійснюється в три етапи:

1. формулюємо задачу мовою математики, тобто будуємо математичну модель;
2. розв’язуємо одержану математичну задачу;
3.      записуємо математичний розв’язок мовою, якою була сформульована початкова задача.

Схематично ці етапи можна зобразити так:

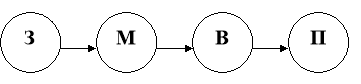
З – дана прикладна задача,

М – її математична модель.

В – відповідь до моделі,

П – відповідь до прикладної задачі.

Перехід від З до М називають процесом моделювання.

Щоб створити відповідну модель, треба знати не тільки математику, а й ту галузь науки чи виробництва, з якою пов’язана дана прикладна задача.

Розрізняють математичні моделі першого і другого роду. До моделей першого роду належать графіки, графи, схеми, числові таблиці, різні кібернетичні моделі. Абстрактніший характер мають надзвичайно важливі для теоретичних досліджень і практики моделі другого роду – рівняння, нерівності та їхні системи.

4. Застосування математичного моделювання.

Учитель. 1) Розглянемо. Як одне й те саме рівняння може відображати перебіг різних процесів.

Трьом групам учнів класу треба скласти математичні моделі до таких прикладних задач.

1. Як можна розміняти 1 грн. на монети по 2 к. і 5к.?

(Нехай х і у – кількість відповідно дво- і п’ятикопійкових монет. Тоді 2х+5у=100.)

2. Два автомобілі перевезли за день 82 т зерна. Вантажність одного автомобіля 8т. а другого – 6т.Скільки рейсів могли зробити автомобілі?

(Нехай один автомобіль зробив х рейсів, а другий  - у рейсів. Тоді 8х+6у=82.)

3. У швейному цеху є 38 м тканими. На пошиття піжами потрібно 4 м тканими, а на халат – 3м. Скільки можна пошити піжам і халатів?

(Нехай х та у – відповідно кількість піжам і халатів. Тоді 4х+3у=38.)

Як бачимо, всі три задачі мають спільну математичну модель – рівняння виду ax+by=c.

2) Розглянемо кілька найпростіших прикладів фізичних процесів. Динаміка яких має такі самі характеристики, і переконаємося, що для того, щоб їх вивчити, достатньо однієї математичної моделі. Так пов’язані між собою заряд конденсатора і напруга в ньому: q=CU; напруга на кінцях провідника і сила струму: U=RI; потік магнітної індукції, який пронизує контур, і сила стуму в контурі: Ф=LI.

Коефіцієнти пропорційності в цих формулах: С – ємність, R – опір, L – індуктивність – сталі величини, які характеризують властивості певної речовини.

Прямо пропорційна залежність моделює також залежність між масою та об’ємом за сталої густини:

m=ρ×V;

залежність між шляхом і часом під час рівномірного руху:

s=v×t;

залежність між довжиною кола та його діаметром:

C=π×d.

Залежність між довжиною стержня і температурою нагрівання описується формулою

l=l₀(1+αt);

між об’ємом газу та його температурою при сталому тиску – формулою

V=V₀(1+βt) – закон Гей-Люссака;

Між швидкістю і часом під час рівноприскореного руху – формулою

v=v₀+αt тощо.

У фізиці кожна із залежностей розкладається окремо, коли вивчається відповідне явище.

Математик, абстрагуючись від фізичної реальності, вводить поняття лінійної функції

y= kx + b, k є R, b є R – математичної моделі перелічених вище явищ й безлічі інших явищ, які мають лінійний характер перебігу.

Квадратична функція y=ax²+bx+c, a0, є аналітичним записом площі квадрата зі стороною a;

S=a²;

площі круга з радіусом r.

S=πr²;

шляху тіла, що вільно падає:

.

3) Розглянемо деякі найпростіші математичні моделі в біології та екології, в яких визначальну роль відіграють елементарні функції.

У біології лінійна залежність між двома змінними величинами зустрічається досить рідко. Проте за певних умов залежність між двома змінними інколи можна описати лінійною функцією.

Наприклад, на певному проміжку часу (зокрема, на ранній стадії) розвитку риби її довжина лінійно залежить від віку :

L=b×t,

де L – довжина, t – час, b – параметр (коефіцієнт пропорційності), який залежить від виду риби і за даними натуральних спостережень.

Цікавішим є застосування в екології дещо складнішої функціональної залежності – так званої обернено пропорційної залежності:

, k – const, х0.

Ця залежність застосовується для математичного моделювання взаємостосунків типу «хижак - жертва». Зокрема такі взаємостосунки мають популяції зайців і вовків. У певній період їх розвитку залежність кількості N  популяції зайців від кількості n популяції вовків може бути виражена функцією

,

де параметр k визначається на основі даних натуральних спостережень. Якщо в якийсь певний момент часу було зафіксовано N=120 і n=30, то k=120×30=3600.

Отже, кількість зайців залежно від кількості вовків можна визначити за формулою:

.

Можна бачити, що чим більше налічується вовків, тим менше буде зайців. Проте слід зазначити, що ця залежність, крім хижацтва вовків, не враховує інших факторів, які впливають на розмноження і смертність зайців. Тому такою залежністю користуватися можна тільки за певних досить жорстоких обмежень і для досить грубого прогнозування.

У наш час математики разом з біологами створили математичні моделі цілих органів людини. У найпростіших випадках – це окремі формули, частіше системи з десятків і навіть сотень рівнянь, які математично виражають діяльність людини, перебіг біологічних процесів. Саме на шляху математичного моделювання вчені бачать визволення людства від ранкової небезпеки, ефективне лікування і профілактику серцево-судинних захворювань

4. Розв’язування задач.

У першому завданні треба лише скласти математичну модель до задачі; другу задачу слід розв’язати, попередньо склавши її математичну модель.

Учнів об’єднують у три групи. Троє учнів (по одному від кожної групи) працюють біля дошки.

Завдання для першої групи

1. Обчисліть об’єм кімнати, якщо її довжина 12,3м, ширина 8,3м, висота 4,3м.

Відповідь. V=12,3×8,3×4,3.

2. У кінозалі 360 місць. У кожному ряді місць на 2 більше, ніж рядів у залі. Скільки рядів у залі і скільки місць у кожному ряді?

Розв’язання

Нехай у кінозалі х рядів, а в кожному ряді у місць. Маємо систему:

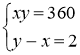
Звідки х=18, у=20.

Відповідь. 18 рядів, 20 місць.

Завдання для другої групи

1.      Учень купив кілька зошитів по 80к. і витратив менше, ніж 3 грн. скільки зошитів він міг купити?

Відповідь. 80х<300, де х – кілька зошитів.

2.      Кубики викладено у рядки так, що у верхньому рядку 3 кубики, а в кожному нижчому – на 2 більше, ніж у рядку над ним. Усього 10 рядків. Скільки кубиків у всіх десяти рядках?

Розв’язання

Кількість кубиків у рядках утворює арифметичну прогресію, у якої        a₁ =3, d=2. Кількість усіх кубиків – це сума десяти перших членів прогресії.

Відповідь. 120 кубиків.

5. Застосування математичного моделювання у прогнозуванні фізичних явищ та об’єктів.

Учитель. Математика дає змогу описати досить широке коло фактів і спостережень. Провести їх детальний аналіз, передбачити, як поводитиме себе об’єкт у різних умовах, тобто спрогнозувати результати майбутніх спостережень. Історія математики знає чимало прикладів, коли в межах удало побудованої математичної моделі за допомогою обчислень, як кажуть «на кінчику пера», вдалося передбачити існування нових фізичних об’єктів.

Учениця. Французький астроном Рубен Левер’є (1811-1877), досліджуючи неправильність в русі планети Уран, тобто відхилення траєкторії планети від тієї, яку вона повинна була б мати за законом всесвітнього тяжіння, висловив припущення про вплив на її рух невідомої планети. Левер’є відправив берлінському астроному Галле (1812-1910) листа, в якому писав: «Скеруйте ваш телескоп у точку екліптики в сузір’ї Водолія на довготі 326°, і ви знайдете в межах 1° від цього місця нову планету з помітним диском, яка має вигляд зірки приблизно дев’ятої величини». Галле отримав листа 23.09.1864 р., у першу ж ніч скерував свій телескоп у вказане Левер’є місце небосхилу і на відстані лише 52’ від нього побачив невідому планету.

Незалежно від Левер’є таке саме передбачення зробив і Джон Адамс (1819-1892). Цей день увійшов в історію науки як день величного тріумфу небесної механіки і математики. З безодні космосу астроном побачив слабкий відблиск диска планети, яку математик «бачив», не поглянувши на небо, за письмовим столом, побачив на основі математичних розрахунків. Її назвали Нептуном. Більше того, формули видали вченому характеристики орбіти за уранової планети, її масу і відстань від Сонця.

За допомогою математичних обчислень американський астроном Персиваль Ловель (1855-1916) у 1915 р. довів існування в сонячній системі дев’ятої планети і розрахував її орбіту. Через 15 років Клайд Томбо за вказівкою Ловелла відшукав візуально і найвіддаленішу планету Сонячної системи, яку назвали Плутоном.

Є легенда, що Аристотель (384-322 рр. до н. е.) помер з відчаю, не зумівши пояснити морські припливи. Ісаку Ньютону (1643-1727) потрібно було на це кілька сторінок у «Математичних началах натуральної філософії», де він застосував відкритий ним математичний аналіз і три закони Кеплера. А Галілео Галілей (1564-1642)  на основі закону всесвітнього тяжіння розрахував час повернення до сонця комети, і вона, як за розкладом, у квітні 1759 р. справді повернулася.

6. Підсумок уроку.

Учитель. Кожна модель зберігає лише важливе для дослідження даного об’єкта і тому ніби очищує, вивільняє потрібну нам інформацію від безлічі інших характеристик, які в даному випадку нас не цікавлять. Тому потрібна інформація фіксується, так би мовити, в чистому вигляді, що дає можливість відразу побачити закономірності, які нас цікавлять, і навіть виявити такі, які поза математичною моделлю залишилися б прихованими, нерозкритими. Учені, які вміли читати закодовану в моделях інформацію, робили визначні відкриття «на кінчику пера». Рівняння чи нерівності щедро розкривали їм таємниці глибинних закономірностей природи, дарувала нові елементарні частинки, планети, чорні дірки, квазари й інші загадкові об’єкти реальної дійсності і відношення між ними.

На уроці з’ясували, як математична модель виникає із реальної задачі і як отримує свій подальший розвиток; ознайомились з тим, як математична модель може бути придатна для класу конкретних задач, а також із застосуванням  математичних моделей у різних галузях науки і техніки.

7. Домашнє завдання.