Урок математики у 6 класі "Розв'язування задач на рух за допомогою рівнянь

Урок  математики в 6 класі

Тема: Розв'язування задач на рух за допомогою рівнянь.

Мета:

•        навчальна: удосконалити набуті знання і вміння розв'язувати задачі за допомогою рівнянь на рух та рух по воді, використовуючи формули руху;
•        розвивальна: розвивати логічне мислення, пам'ять, вміння аналізувати;
•        виховна: виховувати зосередженість, працелюбність, відчуття часу та його раціонального використання.

Тип уроку: закріплення знань, умінь та навичок.

Обладнання: комп’ютер, презентація у форматі Microsoft Office Power Point 2010, роздатковий матеріал.

 

Через рівняння, теореми
Я всякі вирішував проблеми.

Джеффі Чосер (1340(45)- 1400),

є одним з початківців англійскої національної літератури, та літературної мови,першим почав писати свої твори не на латині, а на рідної мові.

 

Те,що я встиг пізнати, - чудово.
Сподіваюся, таке ж чудове те,
Що мені ще доведеться пізнати.

Сократ,

давньогрецький філософ

Хід уроку

І.Організаційний момент.

Вітання, перевірка готовності учнів до уроку.

 

ІІ. Актуалізація опорних знань.

1. Перевірка домашнього завдання.

Самоперевірка за зразком  на проекторі.

  

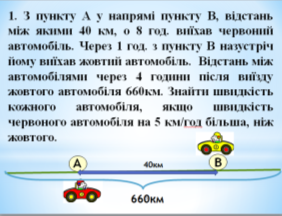
1) З пункту А у напрямі пункту В, відстань між якими 40 км, о 8 год. виїхав червоний автомобіль. Через 1 год. з пункту В назустріч йому виїхав жовтий автомобіль, який був у дорозі 4 год. Відстань між автомобілями 660км. Знайти швидкість кожного автомобіля, якщо швидкість червоного автомобіля на 5 км/год більша, ніж жовтого.

Розв’язання

Нехай х км/год  швидкість жовтого автомобіля. За умовою відстань між автомобілями на початку руху 40км, в кінці   660км.

Складаємо і розв’язуємо рівняння:

5(х+5) + 4х – 40 = 660;

5х + 25 +4х – 40 = 660;

5х +4х = 660 +40 – 25;

9х = 675;

х = 75.

Отже, швидкість жовтого автомобіля 75 км/год,  тоді  швидкість  червоного

автомобіля    75 + 5 = 80 км/год.

Відповідь: 75 км/год; 80 км/год.

 

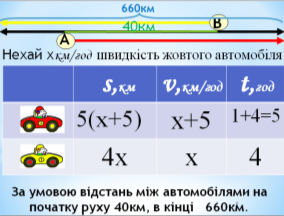
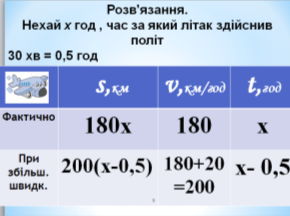
2) Літак виконав рейс між містами зі швидкістю 180 км/год. Якби він збільшив швидкість на 20 км/год, то міг би виконати рейс на 30 хвилин швидше. Знайти відстань між містами.

Розв’язання

Нехай х год , час за який літак здійснив політ

Складаємо і розв’язуємо рівняння:

200(х-0,5) = 180х;

200х – 100 = 180х;

200х -180х = 100;

20х = 100;

х = 5.

Отже,  5 годин – час за який літак здійснив політ. Відстань між містами 180*5 = 900 км.

Відповідь: 900 км.

 

 

2. Математичне лото.

Кожен учень отримує картку з відповідями (два варіанти). Учитель читає запитання, а учні відшукують відповідь у себе на картці та ставлять номер питання.

Варіант 1

розв’язання	протилежний		алгоритм
подібні		корінь
	спрощення	множення

 

Варіант 2

алгоритм	множення		розв’язання
		спрощення	подібні
	корінь	протилежний

 

Питання:

1.     Число, яке перетворює рівняння у правильну рівність. (корінь)
2.     Доданки, що мають однакову буквену частину і можуть відрізнятися один від одного лише коефіцієнтом. (подібні)
3.     Як знайти час, знаючи швидкість руху та відстань? ()
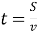4.     Швидкість руху човна за течією дорівнює … ()
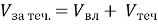5.     Процеси розкриття дужок, зведення подібних доданків, ще можна назвати … (спрощення)
6.     На який знак потрібно змінити знак доданку, що переноситься з однієї частини рівняння в іншу… (протилежний)
7.     Швидкість руху човна проти течії дорівнює … ()
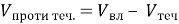8.     Процес знаходження кореня рівняння. (розв’язання)
9.     Швидкість руху човна по озеру дорівнює …()
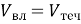10. Як обчислити відстань, знаючи час і швидкість руху? ()
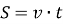
11. Дія, яку виконують при розкритті дужок, якщо за дужками є множник. (множення)
12. Порядок виконання певних дій. (алгоритм)

3. Усні вправи:

• Спростіть вираз:

a) -9m + 3m;        

б) 0,6b – b;      

в) -2 (а + 3);     

г) 0,5 (-х - 3).

• Не розв’язуючи рівняння, знайдіть його корені:

а) 325 + х = 45 + 325;      

б) 2(х-5) = 2*7 – 10; 

в) х +5 = х - 90;

г) 2(3+х) = 2х + 6.

 

ІІІ. Формування теми, мети й завдань уроку. Мотивація навчальної діяльності.

Сьогодні на урок я пропоную таке гасло:

Думати – колективно,

Діяти - оперативно,

Сперечатись – доказово.

Це для всіх обов'язково!

Я сподіваюсь, що це гасло надихне вас на творчу працю.

Тема нашого уроку «Розв'язування задач на рух за допомогою рівнянь».

 

Мета: навчитися розв'язувати задачі на рух за допомогою рівнянь та  відпрацьовувати навички розв'язування.

(Учні записують тему уроку в зошиті)

 

IV. Удосконалення знань, вмінь та навичок.

Загадкове, вам знайоме,

В ньому є щось невідоме.

Його треба розв’язати,

Тобто корінь відшукати.

Кожен легко, без вагання

Відповість, що це… рівняння

Ми з вами повторили деякі теоретичні і практичні питання, тепер можна починати розв’язування задач.

 

Технологія «Мозковий штурм».

 

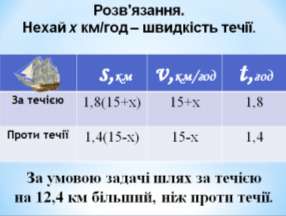
Задача 1. Човен плив 1,8 год за течією  і 1,4 год проти. Шлях, який проплив човен за течією, виявив­ся на 12,4 км більшим від шляху, який він проплив проти течії. Знайдіть швидкість течії, якщо швид­кість човна в стоячій воді становить 15 км/год.

Розв’язання

Нехай х км/год – швидкість течії.

За умовою задачі шлях за течією на 12,4 км більший, ніж проти течії.

Складаємо і розв’язуємо рівняння:

  1,8 (15+х) – 1,4 (15-х) = 12,4;

  27 + 1,8 х – 21 + 1,4 х = 12,4;

  1,8 х + 1,4 х = 12,4 – 27 + 21;

  3,2 х = 6,4;

  х =  6,4 :3,2;

  х = 2.

Отже, швидкість течії річки 2 км/год.

Відповідь: 2 км/год.

Задача 2. Турист пройшов дві ділянки шляху протягом 12 годин. На одній з ділянок він ішов зі швидкістю 4 км/год, а на іншій 5 км/год. Знайдіть довжину кожної ділянки, якщо середня швидкість туриста склала 4,75км/год.

Розв’язання

Нехай х год , час за який турист пройшов І ділянку. Середня швидкість туриста на всьому шляху склала 4,75км/год.

Як знайти середню швидкість? Записати на дошці: v_сер=s_заг:t_заг

Згідно умови можна знайти загальну відстань яку пройшов турист.

4,75 =         s= 4,75*12     s= 57 км

 

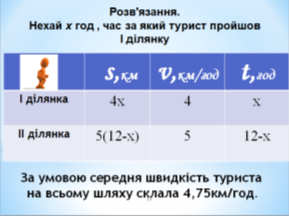
Складаємо і розв’язуємо рівняння:

4х + 5(12-х) = 57;

4х + 60 - 5х = 57;

-х = -3;

х = 3.

Отже, 3 год , час за який турист пройшов І ділянку.

Тоді довжина І ділянки 4*3=12 км, довжина ІІ ділянки 5(12-3)=45 км.

 

Задача 3. Велосипедист проїхав ділянку шосе зі швидкістю 18 км/год і ділянку грунтової  дороги зі швидкістю 12 км/год. Усього він проїхав 78км. Скільки часу велосипедист витратив на весь шлях, якщо по дорозі він їхав на 0,5 год більше, ніж по шосе?

 

Розв’язання

Нехай х год , час який їхав велосипедист грунтівкою. За умовою задачі весь шлях 78 км.

 

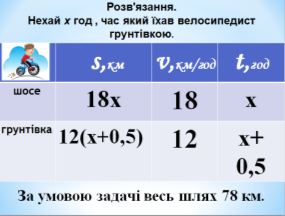
Складаємо і розв’язуємо рівняння:

18х + 12(х+0,5) =78;

18х + 12х + 6 = 78;

18х +12х = 78 - 6;

30х = 72;

х = 2,4.

Отже,  2,4 години – час, що велосипедист їхав по шосе,

2,4+0,5=2,9 (год)  час грунтовою дорогою.

2,4+2,9=5,3 (год) час, який велосипедист витратив на весь шлях.

Відповідь:  5,3год.

 

V. Домашнє завдання.

Кожен учень отримує завдання на окремому аркуші..

№1. Човен плив 1,8 год за течією  і 1,4 год проти. Шлях, який проплив човен за течією, виявив­ся на 12,4 км більшим від шляху, який він проплив проти течії. Знайдіть швидкість течії, якщо швид­кість човна в стоячій воді становить 15 км/год.

№2. Турист пройшов дві ділянки шляху протягом 12 годин. На одній з ділянок він ішов зі швидкістю 4 км/год, а на іншій 5 км/год.

Знайдіть довжину кожної ділянки, якщо середня швидкість туриста склала 4,75км/год.

№3. Велосипедист проїхав ділянку шосе зі швидкістю 18 км/год і ділянку грунтової  дороги зі швидкістю 12 км/год. Усього він проїхав 78км. Скільки часу велосипедист витратив на весь шлях, якщо по дорозі він їхав на 0,5 год більше, ніж по шосе?

Творче завдання

Складіть задачу і рівняння до неї за даними таблиці і розв’яжіть.

	(км/год)	t (год)	s (км)
Пішки	x	2		Разом 38 км
Велосипедом	х + 6	3

 

VІ. Підсумок уроку.

Отже, сьогодні на уроці ми:

• навчалися розв'язувати задачі на рух за допомогою рівнянь;
• ви побачили, що в задачах на рух за х можна приймати відстань, швидкість, час;
•  відпрацювали навички розв'язування рівнянь та виконання арифметичних дій з раціональними числами.

Оцінки за роботу на уроці.

Рефлексія:

 

- дізнався...      - зрозумів...     - навчився...     - найбільший мій успіх - це...

- найбільші труднощі я відчув...      - я не вмів, а тепер умію...    - я змінив своє ставлення до...         - на наступному уроці я хочу...

 

Я хочу дізнатися з яким настроєм ви прийшли до кінця уроку, за моєю командою.

Хто відчуває, що у нього в душі перший смайлик підніміть, будь ласка за моєю командою 2 руки вгору, якщо ваш стан – другий  смайлик, то руки за голову, якщо у вас не дуже хороший настрій, то покладіть руки на парту. І так…

Рівняння – це не просто рівність

З одною змінною чи кількома.

Рівняння – це думок активність,

Це інтелекту боротьба .

Так будьте творчими, активно розвивайтесь,

Долайте труднощі у своєму житті,

Але з рівняннями, прошу, не розлучайтесь,

Вони послужать вам іще у майбутті!

Дякую за урок.